t-test

guoguo

www.rusersplace.com

作者写在前面：

本人是搞生物信息的在读硕士研究生，接触生物信息的有两年时间，学习 R，Linux 命令行。一开始沉迷于各种软件的安装和运行，慢慢发现，程序是现成的，代码也是现成的，稍微修改就能用，甚至有的直接可以用。但是软件，程序的结果却看得一脸懵逼。绕了一个大圈子才发现统计学才是核心，而那些软件、程序只是一个工具，会用就行了。平时遇到什么不懂的东西，各种谷歌，你能想到的问题几乎都能找到答案。用的时候找一下，不用的时候就放下，导致下次用的时候再找，浪费大量时间。所以本人在这里尽可能全面的将我遇到的统计知识整理出来，方便巩固学习，也供大家交流讨论，不对的地方请批评指正。

什么是 t-test?

t-test 也称为 Student's T Test，用来比较两样本平均值之间是否具有显著性差异；

换句话说，t-test 让你知道这些差异是不是偶然发生的。

t-test 的类型：

one-sample t-test，用来比较单个样本平均值和一个给定的平均值（理论值）；
independent samples t-test（ unpaired two sample t-test），用来比较两组独立样本平均值；
paired t-test，用来比较两个相关样本组之间的平均值；

t-value:

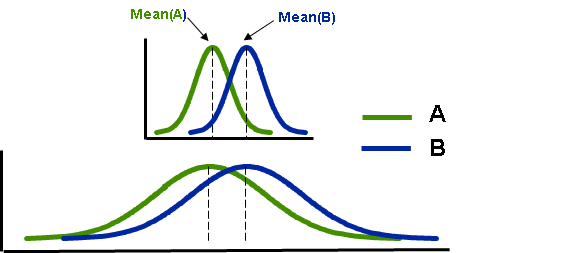
上面的两个图是A、B两组的两种情况的 t 分布图，两种情况中A组样本和B组样本的平均值一样。只是图1中曲线比图2中曲线偏瘦。学过统计的人都知道，瘦表示方差小，胖表示方差大。图1中的A、B的曲线都很瘦，表示A、B的方差（variance）小，组内的离散程度/变异程度小。不过为了方便这里用方差的开方~标准差（standard deviation）来举例说明，如果A表示一组女生的身高，B表示一组男生的身高，mean(A)=155cm，mean(A)=170cm，sd(A) = 5, sd(B) = 10，那么就说明女生的身高在 155±5cm之间波动，男生的身高在 170±10cm之间波动，相比较来说男生的身高波动性较大，变异程度大。

t-value 就是组间差异（difference between two groups）与组内差异（the difference within the groups）的比值。

t = \frac{\bar{X_A} - \bar{X_B}}{SE(\bar{X_A}-\bar{X_B})}

\bar{X_A} - \bar{X_B}：两组样本均值的差值；

SE(\bar{X_A}-\bar{X_B})： standard error of the difference，均值差的标准误（均值标准误的差）。

单样本T检验（one-sample t-test）

t = \frac{m-\mu}{s/\sqrt{n}}

m: 样本的均值

μ: 一个已知的均值（理论值）

s: 样本的标准差（standard deviation）

n: 样本量

R 中的单样本 t-test：

假如我们使用机器制造直径为 10.01mm 的零件，最近制造的一批零件有20个，我们想要知道这批零件的
均值（m）和理论均值μ=10.01是否有明显差异，也就是说生成的这批零件是否符合规格。
#R中使用 rnorm 函数生成符合正态分布的一组随机数
rnorm(n, mean, sd)
n:要生成随机数的数量
mean:要生成该组随机数的平均值
sd:要生成改组随机数的标准差
set.seed(233)
sample <- rnorm(30, mean = 10, sd = 0.05 )
head(sample)
[1] 10.044807 10.036622  9.984592  9.952429  9.982188 10.065807
原假设（Null hypothesis）：
H0: m = μ 该批零件均值m等于理论均值μ。
备择假设（Alternative hypothesis）：
H1: m ≠ μ 该批零件均值不等于理论均值μ；
H1: m > μ 该批零件均值大于理论均值μ；
H1: m < μ 该批零件均值小于理论均值μ。

H0 : m = μ；H1 : m ≠ μ（双尾）

t.test(sample, mu = 10.01)

从结果中可以看出 t = 0.47，自由度 df = n-1 =29，因为 p-value = 0.64 大于 0.05，所以差异不显著，所以接受原假设，认为该批零件直径的均值与理论均值相等，生产的零件符合标准。

H0 : m = μ；H1 : m > μ（单尾）

从上面的双尾 t-test 看出，如果理论均值 μ = 10.01，那么该批零件符合标准。这里我们进行单尾 t-test，备择假设该批零件直径的均值 m 大于理论均值 μ，设置理论均值为 μ = 9.9。

t.test(sample, mu = 9.9, alternative = "greater")

结果中 p-value < 0.05，所以拒绝原假设，认为该批零件直径均值显著大于理论均值 9.9。

H_0 : m = μ H_1 : m < μ （单尾）

这里的备则假设该批零件直径的均值 m 小于理论均值 μ，设置理论均值为 μ = 10.1。

t.test(sample, mu = 10.1, alternative = "less")

p-value < 0.05，拒绝原假设，接受备则假设认为该批零件直径的均值 m 小于理论均值 10.1，该批零件不合格。

独立样本T检验（independent samples t-test）

独立样本 T 检验，首先要服从正态分布。根据两组数据的方差是否相同，分为 pooled variances 和 separate variances。

同方差（pooled variances）t-test

t = \frac{m_A - m_B}{\sqrt{ \frac{S^2}{n_A} + \frac{S^2}{n_B} }}

A 和 B 代表两组要比较的数据；

m_A: A 组数据的均值；

m_B: B 组数据的均值；

S^2 是 A 和 B 两组数据共同方差的估计值：

S^2 = \frac{\sum{(x-m_A)^2}+\sum{(x-m_B)^2}}{n_A+n_B-2}

n_A: A 组数据的样本量；

n_B: B 组数据的样本量。

异方差（separate variance）t-test

t = \frac{m_A - m_B}{\sqrt{ \frac{S_A^2}{n_A} + \frac{S_B^2}{n_B} }}

S_A^2: A 组数据的方差；

S_B^2: B 组数据的方差。

方差的计算方法如下：

S^2 = \frac{\sum{(x-m)^2}}{n -1}

R 中的独立样本 t-test（同方差）

假如我们使用两台机器生产零件，要比较两台机器生产的零件直径的平均值有没有差异，用 R 随机生成
符合正态分布的两组数据 A，B，分别表示 A 机器，B 机器。
set.seed(233)
sample_A <- rnorm(30, mean = 10, sd = 0.05 )
head(sample_A)
[1] 10.044807 10.036622  9.984592  9.952429  9.982188 10.065807
set.seed(333)
sample_B <- rnorm(30, mean = 10.01, sd = 0.05)
head(sample_B)
[1] 10.005859 10.106734  9.907436 10.023887  9.933702  9.996542
我们在这里只进行双尾检验，单尾检验可参考单样本 T 检验，假设如下：
原假设（H0）：两台机器生产的零件直径相同
备则假设（H1）：两台机器生产的零件直径不同

H_0: m_A = m_B ; H_1: m_A \ne m_B （同方差）

t.test(sample_A, sample_B, var.equal = T)

自由度 d_f = n_A + n_B -2 = 58，因为 p-value > 0.05，所以不能拒绝原假设，两台机器生产的零件直径相同。

R 中的独立样本 t-test（异方差）

我们随机产生服从正态分布的方差不同的两组数据：
set.seed(233)
sample_A <- rnorm(30, mean = 10, sd = 0.05 )
head(sample_A)
[1] 10.044807 10.036622  9.984592  9.952429  9.982188 10.065807
set.seed(333)
sample_B <- rnorm(30, mean = 10.01, sd = 1)