(1)
由公式可知,电感上流过的电流是对电感两端电压的积分,电压水平固定时,流过电感的电流的斜率也一定,电压为+24 V时,电流以固定斜率增加,电压为−24 V时,电流以同样的斜率减少,上述电压波形对应的电感电流如
图3
所示。
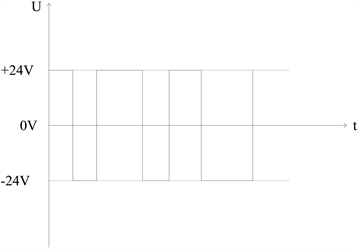
Figure 2
. Voltage waveform on coil load
图2
. 线圈负载上电压波形

Figure 3
. Current waveform on coil load
图3
. 线圈负载上电流波形
由此,可以通过控制高低电平保持的时间,也即是导通角,改变电感电流的形状,使其近似于包含特定谐波分量的电流波形,从而实现多频信号的产生。为了简化计算过程,通常设置输出波形为1/4周期对称波形,即前半个周期和后半个周期镜像对称,在同一个半周期内,前1/4周期和后1/4周期轴对称。
周期信号的傅里叶级数展开式为
(2)
当输出波形为1/4周期对称波形时,傅里叶级数中的直流分量、偶次谐波分量和奇次谐波的正弦分量都为零,从而减少了求解过程中需要的等式,极大地简化了方程和求解过程,简化后的信号傅里叶级数展开式为
为需要抑制的谐波次数的集合。
优化问题的求解目标为使各次谐波分量接近一定调制比时的最佳开关角序列。
2.2. 算法实现
现有单频机器的频率,根据产品的不同,多为50 kHz、150 kHz、300 kHz左右的频率,国外厂商金检机频率范围可达1 MHz。因此,在选择频率的时候,考虑各次谐波分布在50 kHz~1 MHz的范围内,谐波次数太接近会使后续分频处理复杂,难以区分相邻两个谐波分量,太远不利于充分利用中间频率的信息。本实验将FPGA频率设置为24 MHz,选择50.42 kHz作为基频,利用其1、3、7、17次谐波,具体频率如
表1
所示,其中最高次谐波频率为系统频率24 MHz的1/28,通过更改FPGA频率,可以很方便地更改频率组合。

Table 1
. Experimental frequency selection
表1
. 实验频率选择
选定频率后,一个基频信号周期内的FPGA时钟数为28乘以17,即476个FPGA时钟。
利用MATLAB产生一个谐波大小与谐波次数成反比的波形,其表达式如下:
(14)
特定谐波消除算法常用牛顿法求解方程组,但是对于本文中的含不等式约束问题,更适合使用内点法求解,利用Matlab的fmincon函数,可以很方便地求解该类优化问题 [12] [13] 。
2.3. 算法优化结果
优化前后的导通角如
表3
所示:

Table 3
. Conduction angles before and after optimization
表3
. 优化前后的导通角
定义谐波总谐波失真如公式(15)所示
,其中p为谐波次数。优化前后的谐波分量和总谐波失真如
表4
和
表5
所示:

Table 4
. Percentage of harmonic components before and after optimization
表4
. 优化前后的谐波分量占比

Table 5
. THD before and after optimization
表5
. 优化前后的总谐波失真
对比结果可知,优化后的总谐波失真更小,且基波和三次谐波更接近预期值。
3. Simulink电路仿真
编写Matlab代码,通过fmincon函数求解优化后的导通角,求出的导通角作为Simulink仿真电路的输入参数。为了产生控制信号的PWM波,需要将导通角与一定频率和幅度的锯齿波进行比较,使用Simulink中的Repeating Sequence模块产生锯齿波,频率和幅值可通过设置Time values和Output values改变。对于50.42 kHz基频,锯齿波的Time values设置为[0 1.9833e−5],output value设置为[0 360]。其中1.9833e−5即为50.42 kHz对应的周期。
优化算法求解的结果是1/4周期内的导通角,因此在0到π/2之间,通过relationaloperator和logicaloperator比较各个导通角和锯齿波的值,结构如
图5
所示。

Figure 5
. Comparison of conduction angles and sawtooth wave in 1/4 cycle
图5
. 1/4周期内比较导通角与锯齿波
如
图6
所示,比较和逻辑判断的结果可以通过sum模块组合成输出信号,对输出求反产生两路相位相反的控制信号。
由于1/4周期对称波形的对称特征,一整个周期内的导通角都可以通过前1/4周期的导通角求出。生成的锯齿波和其中一路控制信号如
图7
所示,通过光标工具可以看到通过比较导通角序列和锯齿波,产生了固定导通时间的PWM控制信号。

Figure 6
. Generation of two control signals
图6
. 两路控制信号

Figure 7
. Sawtooth wave and control signal
图7
. 锯齿波和控制信号
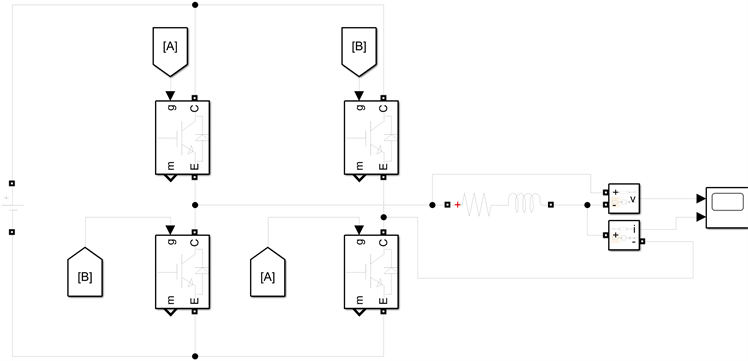
搭建
图8
所示的全桥电路,以A,B两路作为控制信号,用串联的电阻和电感作为负载,直流电源选择24 V。
电阻和电感参数为0.4515欧姆和10e−6亨利,其取值为实测发射线圈参数。
最终在负载上产生的电压电流波形如
图9
所示,幅度为正负的电流波形的分段模拟。
结果显示,在电感负载两端产生了正负24 V的脉宽调制信号,在电感负载上产生的电流波形是对
图4
理想电流波形的分段拟合。因此改变导通角,最终可以实现电流波形的改变,合理设置导通角,可以产生带特定谐波分量的电流信号。
图8
. Simulink全桥电路
图9
. Simulink仿真结果
4. 硬件电路设计与实现
4.1. 硬件系统
多频信号的硬件实现需要以下几个部分:FPGA开发板、H全桥及其驱动电路、金属检测探头的发射线圈。
Matlab计算出所需要的导通角,并且转换成与24 MHz相对应的时钟数。编写FPGA代码,在固定的时钟边沿输出H全桥控制信号。所使用的FPGA系统时钟为50 MHz,因此使用PLL IP核产生24 MHz时钟。时钟配置完成后,在顶层文件实例化该模块,一个基频周期包含476个FPGA时钟,对24 MHz时钟进行计数,在每个导通角对应的时钟上升沿进行输出电平高低翻转,另一路输出对其取反,两路输出即为H桥驱动芯片的输入信号,使驱动芯片产生反相的MOS管控制信号,最终在发射线圈上产生电平为正负24 V,具有固定导通角的PWM波形。
硬件电路主要包含H全桥及其驱动电路和电源部分。由于24 V直流电源使用广泛,容易获得,因此全桥驱动电压选择24 V,使用DCDC模块,将24 V电压转换成12 V,作为驱动侧芯片供电。
H桥电路由一对PMOS和一对NMOS组成,但由于PMOS是空穴导电,导通电阻较大,开关速度不如NMOS,且可选型号少,价格偏高,因此为了减小导通时MOS管产生的功率损耗,实现更高的开关频率,常采用四个NMOS实现的全桥电路拓扑。
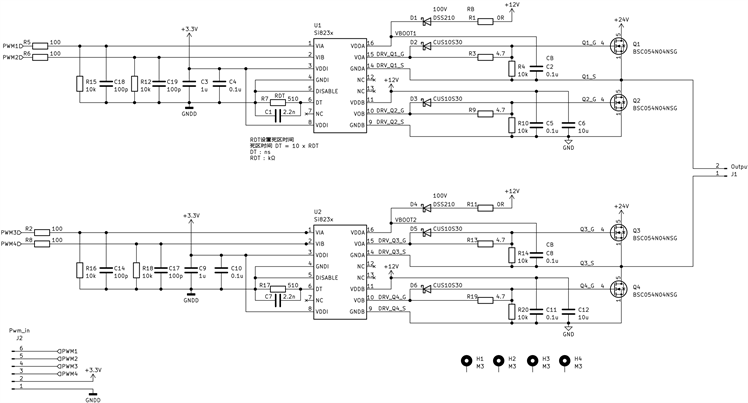
具体电路如
图10
所示。
图10
. 硬件原理图
NMOS的导通条件是,栅极电压比源极高出至少4.5 V (以FDMS8880为例),有的MOS管需要10~15 V才能导通。当时用4个NMOS的全桥电路时,上管导通时的源极和漏极相连,电压相等,因此源极电压也等于直流电源电压,本实验中为+24 V。为了使NMOS保持导通,NMOS的栅极电压需要比源极更高。在电路设计中,24 V已经是电路板上最高电压水平,因此使用自举电路来产生一个比直流电源更高的电压用于导通NMOS上管。
实际使用时,先导通下管,导通时下管的漏极电压为0 V,此时二极管导通,电容通过VCC电源充电,充满电后,VBOOT电压为+12 V。当下管截止,上管导通时,上管源极电压为H桥驱动电压,即+24 V。电容放电,VBOOT在驱动电压的基础上叠加电容电压,产生36 V (24 V + 12 V)的电压,此时自举电路的二极管反向截止。电容电压经过两个电阻分压之后加到上管的栅极和源极,使上管满足导通条件,从而能够持续导通。
4.2. 硬件测试结果
FPGA控制信号如
图11
所示。
图11
. FPGA输出控制信号
在探头的发射线圈两端测得的电压波形如
图12
所示,在线圈两端,产生了幅度为正负24 V,导通角可控的PWM波形,根据理论分析,该波形可以实现发射线圈上的谐波分量可控的多频电流信号。
图12
. 负载两端电压波形
5. 结论
实验基于国内现有金属检测机精度和分辨能力不够高的问题,通过对1/4周期对称波形数学表达式的分析,建立了求解包含1,3,7,17次谐波分量的输出波形的数学模型。通过Matlab求解优化问题,得到一组导通角数据。在Simulink搭建控制信号模块和全桥电路模块,对求解的导通角进行验证,仿真结果表明:可以通过给线圈施加所求导通角的PWM波,在线圈上产生谐波分量可控的电流信号,优化后的导通角产生的波形谐波失真更小,且1,3次谐波分量更靠近期望值。基于理论分析和电路仿真结果,编写了FPGA代码,产生控制信号,设计了全桥电路及其驱动电路,最终在线圈上实现了目标电压信号,从而实现金属检测机多频发射信号的产生。
文章引用
王 倩,李丕丁. 基于谐波抑制的多频信号的仿真与实现
Simulation and Realization of Multi-Frequency Signals Based on Harmonic Suppression[J]. 建模与仿真, 2023, 12(06): 5497-5509.
https://doi.org/10.12677/MOS.2023.126499
参考文献
-
1. 王玉琦, 韩海燕, 郝智慧. 金属检测器在食品工业中的应用[J]. 长春大学学报, 2007, 17(2): 71-73.
-
2. 周茂林, 项安. 全数字食品金属检测机信号处理系统仿真[J]. 计算机仿真, 2013, 30(9): 208-212.
-
3. 白树忠, 董春阳. 平衡线圈式高精度金属检测算法[J]. 山东大学学报(工学版), 2017, 47(4): 83-88+95.
-
4. Haimovich, H., Marelli, D. and Sarlinga, D. (2020) A Signal Processing Method for Metal Detection Sensitivity Improvement in Balance-Coil Metal Detectors for Food Products. 2020 IEEE International Conference on Industrial Technology (ICIT), 30, 4091-4106.
https://doi.org/10.1109/ICIT45562.2020.9067312
-
5. 周若臣, 洪然, 孔笑荷. 镀铝膜包装的食品金属检测技术[J]. 计量与测试技术, 2021, 48(2): 46-54.
-
6. 刘笑宇. 消谐算法及在多电平逆变器中的应用[D]: [硕士学位论文]. 北京: 北京交通大学, 2014.
-
7. Dahidah, M.S.A., Konstantinou, G. and Agelidis, V.G. (2015) A Review of Multilevel Selective Harmonic Elimination PWM: Formulations, Solving Algorithms, Implementation and Applications. In IEEE Transactions on Power Electronics, 30, 4091-4106.
https://doi.org/10.1109/TPEL.2014.2355226
-
8. Li, L., Czarkowski, D., Liu, Y.G. and Pillay, P. (2000) Multilevel Selective Harmonic Elimination PWM Technique in Series-Connected Voltage Inverters. Indus-try Applications, IEEE Transaction, 36, 160-170.
https://doi.org/10.1109/28.821811
-
9. 高丽辉. 基于选择性谐波消除技术的电磁测深激励方法研究[D]: [博士学位论文]. 长春: 吉林大学, 2020.
-
10. 陈乾. 谐波对电网的影响及其解决措施[J]. 城市建设理论研究(电子版), 2012(5): 1-5.
-
11. 李树鑫, 李艳洁, 董悦坤. 消除高次谐波对电网的影响[J]. 电力电容器, 2002(2): 17-20.
-
12. Napoles, J., Le-on, J.I., Portillo, R., Franquelo, L.G., and Aguirre, M.A. (2010) Selective Harmonic Mitigation Technique for High-Power Converters. IEEE Transactions on Industrial Electronics, 57, 2315-2323.
https://doi.org/10.1109/TIE.2009.2026759
-
13. Nesterov, Y. and Nemirovskii, A. (1994) Interior-Point Polynomial Algo-rithms in Convex Programming. SIAM Review, Philadelphia.
https://doi.org/10.1137/1.9781611970791