Zeta函数的导数生成元当且仅当为常量时存在线性相关

Zeta函数的导数生成元当且仅当为常量时存在线性相关（下）

文/罗莫

摘 要： 本文通过化约偶数不等量分割方程，经数乘逆运算得到不可约整系数多项式方程，可知奇数互素解集是其本原解（由伯特兰-切比雪夫定理推得）；经点乘逆运算得到奇素数多项式方程，可知奇素数基础解系是偶数不等量分割方程的最简本原解。由于可表偶数方程就是关于全集偶数的最简本原解方程，故与可表偶数互补关系的例外偶数的通解就一定是空集，从而证明了二元加法运算在可表偶数上封闭。由于此引理获证，可多米诺骨牌式地解决哥德巴赫猜想、斋藤猜想、孪生素数猜想、波利尼亚克猜想、莫德尔猜想、比尔猜想、abc猜想、奥波曼猜想等系列相关问题。黎曼猜想因与素数分布紧密关联，故借此引理，通过分析Zeta函数当且仅当其通项导数为f（1/2）时的交错级数其正负项“两类发散和”的绝对值（解析延拓已扩域出负数项级数）经洛必达法则可得到与哥猜命题等价，故“两类发散和”存在同构关系，而导数f（非1/2）时扩域出的交错级数其“正负发散和”的绝对值，仅存同态关系，由哥猜推论得到。可见是用哥猜获证做引理，证明了黎曼蔡塔函数通项导数的生成元非1/2时必无0点非平凡解，黎曼猜想获证。本文是对希尔伯特第八问题的全面阐释，囊括了哥德巴赫猜想、孪生素数猜想和黎曼猜想三大部分，解决这些问题的核心，正是希尔伯特的内积思想。

关键词： 可表偶数 例外偶数 素数基础解系 通解 不等量分割 互素 互异同态 同构 线性相关 线性无关 解析延拓 差分算子 通项导数

二元加法运算在可表偶数上封闭，该命题可用偶数不等量分割方程的素数基础解系与通解之间的内积逆运算以及伯特兰-切比雪夫定理来获得证明。尤其是可表偶数和例外偶数与素数基础解系之间存在着一荣俱荣一损俱损的紧密关联。可表偶数与例外偶数的互补定义，决定了例外偶数无素数基础解系，例外偶数的通解也就成了空集。而可表偶数就责无旁贷地囊括了全集偶数的通解，于是哥猜获证。从而证明了可表偶数的数乘封闭或点乘封闭，即二元加法运算在可表偶数上不存在数域扩张和数域缩减，故等式两边解集同构。而非二元加法运算在可表偶数上虽能确定不扩域但无法保证不缩域，故等式两边解集同态。该引理获证，可解决黎曼猜想。黎曼猜想的本质同哥猜一样，无生成元的生成对象不存在，无根系的生命体不存在，无成本的利润不存在。

（上接2.1.）

3.0.蔡塔方程的二项式展开出现变量导数

用复指数变换证明临界线外没有非平凡0点解。根据复指数变换，存在以下等式关系：

ζ（ s ）=∑（ n - s ) =∑ n-1/2 （cos ln n + n-1/2 isin ln n ）^- b =1/√1（cos ln1 +1/√1isin ln1）^- b +1/√2（cos ln2 +1/√2isin ln2）^- b +1/√3（cos ln3 +1/√3isin ln3）^- b +1/√4（cos ln4 +1/√4isin ln4）^- b +…… =0（其中 s =1/2+ b i）。

根据二项式定理展开 ζ（ s ） = ∑1/√ n (cos ln n +1/√ n isin ln n )^- b = ∑｛1/√ n (cosln n ^ （ - b） +C(- b ,1)cos ln n ^(- b -1)·1/√ n· isin ln n +C(- b ,2)cos ln n ^(- b -2)·1/√ n· isin ln n ^2+...+C(- b ,- b -1)cos ln n· 1/√ n ·isin ln n ^(- b -1)+1/√ n· isin ln n ^ （ - b） ｝。

ζ（ s ）= [1/√1(cosln1^ （ - b） ]+[C(- b ,1)cos ln1^(- b -1)·1/√1 · isin ln1]+[C(- b ,2)cos ln1^(- b -2)·1/√1 · isin ln1^2]+...+[C(- b ,- b -1)cos ln1 · 1/√1·isin ln1^(- b -1)]+[1/√ n· isin ln1^ （ - b） ]+[[1/√2(cosln2^ （ - b） ]+[C(- b ,1)cos ln2^(- b -1)·1/√2 · isin ln2]+[C(- b ,2)cos ln2^(- b -2)·1/√2 · isin ln2^2]+...+[C(- b ,- b -1)cos ln n· 1/√ n ·isin ln n ^(- b -1)]+[1/√ n· isin ln n ^ （ - b） ]+……+[1/√ n (cosln n ^ （ - b） ]+[C(- b ,1)cos ln n ^(- b -1)·1/√ n· isin ln n ]+[C(- b ,2)cosln n ^(- b -2)·1/√ n· isin ln n ^2]+...+[C(- b ,- b -1)cos ln n· 1/√ n ·isin ln n ^(- b -1)]+[1/√ n· isin ln n ^ （ - b） ]。

当Res=1/2时，ζ（ s ）=0 有无穷个非平凡0点解，哈代等已证。

从以上黎曼蔡塔函数变换式不难发现，实部和虚部的收敛性质相似，解析延拓后，偶数项数列出现负数值，可正负交错条件收敛于0，虚部取0、实部取负偶数时，级数收敛于0的，这是平凡0点解。根据已知证明，实部取1＞Res＞0的偶实数时，即临界带上存在有正负号的解析延拓交错级数，具备条件收敛，这是非平凡0点。我们来看zeta函数的实部和虚部的通项表达，而不是定义域实部Res的通项表达：

Fr（n）=C(- b ,0)1/√ n (cosln n ^ （ - b） ）(实部常数Res=a为 n 的指数，这里的a=1/2)

Fi（b）=C(- b ,1)1/√ n（ cos ln n ^(- b -1)） · isin ln n

对以上两式进行求导，系数1/2就会显示出来，这就说明了，线性算子作用素数多项式，再经作用后，就会与多项式的均值同构等价。实部常数的倒数乘以均值可还原得到多项式。

其实还可以通过差分算子（相当于离散量中的导数）来证明黎曼蔡塔函数非平凡0点解只对应实部为常数。实部求导，就是实部的差商算子△Fr（n）了，可得到重要系数-1/2,由此可得到特征值的函数2，即导数的函数2。

切萨罗和、阿贝尔和、拉马努金和，都是解析延拓和，这些都不是普通级数求和，普通级数求和不能违背黎曼级数重排定理，条件收敛不可使用交换律和结合律，但解析延拓求和允许条件收敛的重排，开放了对其中任意类无限数列使用结合律，仍不能使用交换律，并引入了均值概率计算。从这些定义规则中，不难理解，解析延拓求和，就是线性算子作用下的自然数级数与负数项特征数作用下的自然数级数（含均值）两者之间的求和以及迭代 n 次的高阶求和。

我们来看自然数的求和，高斯的办法是，先求出自然数的均值（1+ n ）/2，再乘以自然数均值的个数n，就可得到和值，均值的个数n就是特征值的函数，负数项特征值作用下的自然数级数（含均值），就可以理解成特征值的函数作用下的级数均值。素数一次二项式或多项式的线性算子是（ a，b ）或（ a，b ，…）， a 和 b …都属于 n ，特征值的函数是 k，k 也属于 n ，均值是（1+n）/2。线性算子作用下的自然数级数减去特征值的函数作用下的均值，特征值的函数作用下的均值在二项式时不就是2作用 n 吗？在三项式时不就是3作用 n 吗？在多项式时不就是 k 作用 n 吗？素数一次二项式，素数一次三项式，素数一次多项式，在线性算子的作用下，其和值在较大值时一定是2 n 或2 n +1，可见两边的数列通项只有在素数一次二项式时是左右同构（相互蕴含），两边相减可等于0，其它情形左右同态（单向蕴含），两边相减则不等于0。

整数域有这样的性质，有理数也同样有这样的性质，因为整系数多项式可合理生成有理数以及代数数，因此线性算子在代数数数域里，且特征值的函数为2时，zeta函数存在收敛于0，特征值的函数非2时则不存在收敛于0。凡给定的通项表达，所有的代数数系数多项式都可以等价变换得到整系数多项式，当简化到线性算子作用素数一次二项式时，负项数列的特征值的函数是唯一的，改变它，等式左右互素的关系就会改变。

实部常数的倒数，是分子为1时的分母数，当该分母数取大于1/2的分母2时，二项式级数展开后的每个自然数含i的各项，系数会发生加速递减变化，本来实部指数趋于0的多项式，此时便不能趋于0，多项式的绝对值会随着实部常数的递减而远离原来的绝对值0差值，使差值绝对值增大。实部常数的倒数，是分子为1时的分母数，当该分母数取小于1/2的分母2时，二项式级数展开后的每个自然数含i的各项，系数会发生加速递增变化，相当于系数通项式的导数发生变化，本来实部指数趋于0的多项式，此时便不能趋于0，多项式的绝对值会随着实部常数的递增而远离原来的绝对值0差值，使差值绝对值增大。关于这个性态，通过线性代数以及数学分析可以获得证明。

函数A>B,函数B>C，函数A的极限是X，函数C的极限也是X ，那么函数B的极限就一定是X，这个就是夹逼定理。以下是夹逼定理的推论，b的邻域递增改变量△b的绝对值单调递增其函数值越远离A且单调递增，b的邻域递减改变量△b的绝对值单调递减其函数值越逼近A且单调递减。那么根据夹逼定理，b的函数极值等于A。并判定b+△b与b-△b之间有函数极值。因为b+△b的极限是A,b-△b的极限也是A,而b在两数之间，故b的极限定是A。此定理与夹逼定理不同点在，它是通过单调递增和单调递减来获得最小改变量区间的。它不能精准算出极限值，但可以不断获得最小区间有极值存在。比如四三不靠，三心二意，都是用区间判定极值的语言，圆周率π就是四三不靠，自然底数e就是三心二意，重力系数g就是九天之上，浓缩实部常数r就是地平线下，精细结构常数a就是七上八下，黄金分割率 Ф 就是天地之间，费根鲍姆常数δ就是四舍五入，普朗克常数 h 就是六道之外，财富二八律b就是八风不动，五行周期数w就是黎明之际。

通过夹逼定理的推论算法，我们可以逼近算出zeta函数紧邻的新的非平凡0点解，可以通过划定区间用有限步算出单调性，从而判定是否蕴含新解。模长定向变化，转幅定向变化，以保持实部不变，0点条件下延伸时会靠近一个新的虚部值，再继续延伸时，就会越来越远离该新的虚部值，可见在此区间存在一个新的虚部极值。可以用数学归纳法证明，这样的算法是可持续的。这也只能证明虚部可紧邻延伸无限个解在临界线上，还不能证明0点非平凡解都在1/2的临界线上。

3.1.通项导数（差分算子）当且仅当 Re s= 1/2 时存在线性相关

黎曼假设的奥秘是，蔡塔方程的多项式连和只有一个系数选项可以同构表达2 n ，有同构关系才可构造解析延拓后的非平凡0点解，否则同态关系时多项式只能构造不等式。

这个线性代数的思想就是：在原函数求和与负扩域函数求和两者相加的多项式方程中，若实部Re s 所在位置是多项式方程系数向量平直的一维直线斜率，所对应的级数向量线性组合是线性相关的，那么斜率加改变量的级数向量线性组合就是线性无关的；若改变量Re s 所在位置是多项式系数向量弯曲的高维流形导数，所对应的级数向量线性组合是线性相关的，那么导数加改变量的级数向量线性组合就是线性无关的。

因为斜率是导数或高阶导数的生成元，在亚纯函数中，互异斜率会对应互异导数，互异斜率会对应互异函数，自然互异导数会对应互异函数。这个性质可由洛必达法则推导得到。如果不能得到常数，还可以迭代多次，进行多阶求导。

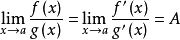
Zate函数虚部ims的所有解都是与离散点有一一映射关系的极值点，故称是弱解析的连续量。原函数与负扩域函数的极值之比等于 A, 即f（ x )- A g( x )=0,-1/ A f（ x )+g( x )=0,g( x )为扩域函数。 A 就是zeta函数指复数函数的实部为1时的均值函数的特征数，其中扩域函数就是均值函数。特征数生成元改变为A+△A，则f（ x )就发生改变，f（ x )- A g( x )也随之发生改变，也就是说会等于非0。

这个结论可由选择公理来印证，新算法会带来新的数集，满足超限数学归纳法，而强连续量本文不予探讨。

含正弦值因子项的都是虚部，显然当每项有两处因子的指数发生变化时，可等价于级数系数因子的导数发生变化，或者说，级数系数因子的曲率相关量发生变化，这个变化量因子系数，我们管它叫导函数向量，该导函数向量跟级数向量的线性组合除有一个切点斜率满足线性相关外，其它都是线性无关的。

根据通项导函数未变化前，级数的每一项都是剩余项向量的线性组合，可知原系数向量跟级数向量的线性组合是线性相关的。这个可由哈代证明过的蔡塔函数存在无穷个非平凡0点解而得到证实。

同构关系的多项式，各项经数乘和内积运算变换后，多项式的解集仍然还可以是同构关系，因每一次都是纯量数乘，但同构关系的多项式，各项经用导数性质的对象叉乘和点乘变换后，多项式的解集立马都变成同态关系了。原级数的线性相关就会变成线性无关了。数乘是各项均衡变换，故可延续同构关系，内积是各项不均衡变换，但可做到互补均衡，故也可延续互补关系，但导数的内积和数乘就没有这样的性质，它不是各项的均衡变换，也不是各项互补但左右总量均衡的变换，它是随着各项变量而加速变换的量，由于导数的马太效应，使大值更大，小值相对更小的性质，同构关系的均衡不再继续。

4.0.线性相关的通项导数（差分算子）若微调一下立马变线性无关

既然原级数系数向量是线性相关的，又已知该级数线性组合不是通过极限获得0值的，只能是正负值抵消得0，即解析延拓后新产生的正负交错级数从而有了条件收敛。因此可判定，正值项级数和与相反的负值项级数和，相加后会得0。因为一阶素数二项式时存在偶数同构关系，这是哥猜引理。不通过这个引理，用导数互异就导致函数互异，函数互异就导致导数互异来证明，线性相关的通项导数（差分算子）若微调一下立马变线性无关。

我们来看zeta函数的差分算子。不难发现高阶素数多项式的差分算子，其重要生成元是素数的项数，即特征数，也就是导数差商 A 就是斜率。当项数超过2时，差分算子就不是原斜率了，而是加上了改变量的斜率或者是加上了改变量的相应导数，正负项不再是原等值变化的单调递增，而是一边越来越大。那两边就是同态关系了，故求和相减后不能收敛于0。

只有差分算子等价于一阶素数二项式时，zeta函数才是正负同构等价的。

f（ x ）的 n 阶向前差分公式为：

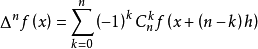
当系数向量的通项式导数因子发生变化后，级数较小项与级数较大项的和值就会随之发生变化。因为级数系数多项式的导数单调性变化会随着级数值的导数增大而加倍增大，于是级数正负项的和值绝对值增大。由于导函数在各正项值和各负项值上的缩放能力因项值不同而不同，故除1/2外的级数各项指数无论怎么变化，级数的和值都不能得0，因此级数各项指数1/2外的导数所构造的系数向量，必跟级数向量的线性组是线性无关的。

通过差分算子的通项再算差分算子，不断迭代进行，就会得到差分算子常数，这个算法也可以用洛必达法则进行多阶求导运算，得到常数 A ,或其中一个重要公因数。对zeta函数求导，会得到重要斜率常数1/2，可见实部常数Res=1/2是zeta函数中导数的生成元，改变1/2就是改变zeta函数中导数的生成元，Res互异，zeta函数的导数即互异。导数互异，求和所得到函数就互异。原1/2对应函数0点，非1/2就对应函数非0点。

在多项式原函数求和与负扩域函数求和两者相加的多项式方程中，我们把负扩域求和看成是纯负扩域求和，是特征数为1的均值数函数求和。而原函数的斜率是1/2,把方程左边的斜率移到右边就变成斜率是2的均值函数，这就与哥猜引理一致了：线性算子作用素数一次二项式与特征数作用多项式均值等价。

若不用这个等价关系证明，可用洛必达法则得到，若斜率互异，则导数互异，导数互异则斜率互异，而导数互异，原函数必互异。当然原函数互异，解析延拓后求和值即原函数减去均值函数的差值也必互异。现已知斜率为1/2时，原函数减去均值函数的差值为0，并有无穷组虚部解，哈代已证，根据互异关系，可得，斜率为非1/2时，解析延拓后求和值不能为0。

于是不含1/2常数的导函数向量，跟级数线性向量的线性组必线性无关，此时的黎曼蔡塔函数就没有非平凡0点解。也就是说，当Res＞1/2,Res＜1/2时,zate函数都没有非平凡0点解。这个结论获证，说明所有的解都在临界线上，于是黎曼猜想就得证。

这一线性规律与哥猜引理很相似。只不过哥猜引理更明确，线性相关的特征数是2，而这一线性规律是建立在假设的基础上的，若函数的生成元 k 有线性相关，则函数的生成元 k +△ k 就线性无关。现在已知哈代证明了有无数个解在临界线上，故生成元Res=1/2存在线性相关，即有0点非平凡解，那1/2+△ k 就线性无关，无0点非平凡解 。 如此可证明，所有解都在临界线上了。于是也就可以反过来证明，线性相关的特征数是2，这就可推理出，例外偶数是空集，线性变换不扩域，据此就可以证明，哥猜也成立了。可见哥猜，孪生素数猜想与黎曼假设三者之间是可以相互证明的等价命题。

4.1.黎曼猜想获证的逻辑导图

总结下黎曼猜想的证明：

1、哈代已经证明黎曼猜想有无穷组解落在1/2的临界线上(解集的无穷性已获证明，解集的无漏性尚待证明）。

2、黎曼猜想的所有解集必须落在Re s =某一常数的直线上，且在0＜Re s ＜1临界带上。介绍须用新数学工具邻函数。

3、除二元运算与匹配的数乘2 m 同构外， k 元加法运算仅与所有匹配的数乘 km 同态而不能同构,从而宏观上证明了复变量Res=1/ k （ k≠2 ）时都无法构造出0点解。多元分割全集对象的2倍有同构关系，多元分割全集对象的 k 倍仅有同态关系，这是黎曼假设成立的关键内核。当年黎曼提出该猜想就是为了试图求证哥猜而变换出的一个表达式。由此可证明，zeta函数所有值域解集若是一个常数，则zeta函数映射的所有定义域实部解集也必是一个常数。

4、zeta函数的值域若解集为唯一常数，则对应函数的实部解集为唯一常数。故临界线外的解集都不是0点解，zeta函数0点上的所有解集就只能在临界线上。zeta函数值是常数，实部值即常数，zeta函数值取互异常数，实部值亦必取互异常数。实部常数与zeta函数收敛值是双射关系。以此结论找到哥猜与黎曼猜想之间的关联，可推理出黎曼猜想获证。这是第一种证明。

5、用二项式定理展开公式变换表达黎曼蔡塔函数中的指数复变量。结果显示了Re s 常数在系数向量中的相关位置若是一维平直的斜率关系，若斜率改变，则函数改变；若是高维弯曲的导数关系，若导数改变，则函数改变。函数系数向量各分量改变斜率因子可以让线性相关的线性组合不再继续线性相关，但系数向量各分量改变导数因子同样不可以让线性相关的线性组合继续线性相关，而是全部变成了线性无关。

6、我们来看zeta函数的差分算子。不难发现高阶素数多项式的差分算子，其重要生成元是素数的项数，当项数超过2时，差分算子就不是可同构的斜率函数了，由斜率生成元构造的导数也是如此，正负项不再是等值的单调递增，而是一边越来越大。那两边就是同态关系了，故求和相减后不能收敛于0。最后通过洛必达法则和解析延拓性质推导该命题为真。

7、只有特征数的倒数与满域的差分算子相继作用一阶素数二项式等价于素数二项式的均值时，zeta函数才是正负同构等价的。而满域的差分算子可从二项式展开中显示出。通过泛函互异的性质，证明了zeta函数实部互异，则函数互异，其中的桥梁是斜率互异则导数互异，导数互异则原函数互异，原函数互异，zeta函数互异。由此证明了实部取非1/2时，函数值不会等于0，也就没有0点解。黎曼猜想得证。

8、黎曼蔡塔函数中指数复变量的实部一旦取非 1/2 值时，即无0点解，从而证明了黎曼蔡塔函数的所有解都落在了 Re s =1/2 的直线上。于是黎曼猜想用第二种方法也就获得了证明。然后总结了，两种封顶证明的思路。前者用哥猜做引理证明黎曼假设，后者用定义域和值域之间互异光滑的连续关系证明了黎曼假设，可反过来证明哥猜。

也就是说，当且仅当Re s =1/2时ζ（s）=1+1/2 S +1/3 S +…才有同构的 k i增广级数系数项或连和后的增广级数系数项，唯有系数 ki 或若干项之和的核函数系数 ki 等于2时，才存在级数解析延拓后等式的左右正负同构，而等于2 k 时则左右同态。有了同构关系，级数的增广线性组才具备线性相关。考察复指数变换后的级数方程通过解析延拓可知，Re s =1/2在表达式中的各项位置(非独立于自变量而受控于自变量)显示,如果Re s 作为改变量不是常量斜率而是变量导数，除非是一维斜率尚可以延续同构关系。但如果其实质是担当了多维导数，稍加改变则会立马破坏级数方程的左右解集同构关系，而转为同态。

因为整数不等量分割方程，其最简本原解是 p + q =2 m， 右边反映特征数和多项式均值的函数，可对应全集偶数，然后再分割互素表达，等式左右通解皆沦为同态关系，即左右可表达的解集不再一样多了。如方程 p + q+r =3 m 左右不是同构的 ， 方程 p + q+r+s =4 m 左右不是同构的 ， 左边无论多少项分割都不是左右同构的，只要右边的系数非2，任意二元或多元分割都不是左右同构的, 而同态关系的增广项连和与其它级数各项连和是不可能有线性相关的，黎曼蔡塔级数方程也就没有非平凡0点解。于是黎曼猜想获证。

一句话，多项式与单项式之间的同构关系稀有，这是黎曼猜想难以攻克的奥秘。现在我们终于搞清楚了希尔伯特第八问题之谜，哥猜、孪生素数猜想与黎曼假设三个问题全是等价的。其中哥猜最为深刻，最有积极意义。

文献参考：

【1】《抽象代数引论》，陈引兰、施恩伟、左可正，科学出版社。

【2】《数论概论》，（美）JosephH.Silverman，机械工业出版社。

【3】《 伽罗瓦理论——天才的激情》，章璞，2013年高等教育出版社。

【4】《线性代数第二版》，郝志峰，2003年高等教育出版社。

【5】《哈代数论》，哈代，2009年人民邮电出版社。

【6】《近世代数概论》，(美)伯克霍夫(Birkhoff G.)(美)麦克莱恩(Mac Lane S.)，人民邮电出版社。

【7】《加性数论（经典基）》，纳森，2012年，世界图书出版公司。

【8】《深圳基础理论原创文集》（数学物理卷），汪斌主编，2017年海天出版社。

注释：

①欧拉乘积公式是 Leonhard Euler (1707 - 1783) 于 1737 年在一篇题为《对无穷级数的若干观察》的论文中提出并加以证明的，式中 n 为自然数，p为素数。Euler乘积公式将一个对自然数的求和表达式与一个对素数的连乘积表达式联系在一起，蕴涵着有关素数分布的重要信息。为了纪念 Riemann 的贡献，Euler乘积公式左端的求和式被冠以Riemann的大名，并沿用Riemann使用过的记号ζ(s)， 称为Riemann ζ函数。

②一个群G的置换表示是群作为一个集合的置换群的群表示（通常该集合有限），并且可以表述为置换矩阵，一般在有限的情形作此考虑－这和作用在有序的线性空间基上是一样的。每个群G都与一个变换群同构，每个有限群都与一个置换群同构。

③德国数学家黎曼(1826~1866)观察到，素数的频率紧密相关于一个精心构造的所谓黎曼蔡塔函数ζ(s)的性态。著名的黎曼假设断言，方程ζ(s)=0的所有有意义的解都在一条直线上。这点已经对于开始的1,500,000,000个解验证过。证明它对于每一个有意义的解都成立，它其实是一曲有关素数分布的神秘乐章，虚部值bi呈现出素数分布的谐波。

④用一因变量依次更替某个有序数对中的元素，叫轮值变换。因变量的一个相邻递增能带来一组自变量的相邻递增。自变量的相邻递增能带来新增因变量的相邻递增，而不仅仅是组合新增的，叫龙头自变量。

⑤极坐标。在平面内取一个定点O， 叫极点，引一条射线Ox，叫做极轴，再选定一个长度单位和角度的正方向（通常取逆时针方向）。对于平面内任何一点M，用ρ表示线段OM的长度，θ表示从Ox到OM的角度，ρ叫做点M的极径，θ叫做点M的极角，有序数对 (ρ,θ)就叫点M的极坐标，这样建立的坐标系叫做极坐标系。本文的极坐标有所改进，从极中心出发的螺线的根数为极径长的读数，螺线的相邻区分格点为螺线长的读数，其中极径长的读数可以为有限值也可以为无限值，转换为笛卡尔坐标系时的y轴读数是原极径长读数的倒数。

⑥我们把这种有顺序的两个数A与B组成的数对叫做有序数对（order pair），记做（A,B），常用在平面直角坐标系中。

⑦格奥尔格·康托尔（Cantor，Georg Ferdinand Ludwig Philipp，1845.3.3-1918.1.6）德国数学家，集合论的创始人。