Python环境下应用Cplex求解最优化问题——docplex


1.前提
1.1基本
这里,我们默认已经知道线性规划,会python语法并已经安装好pycharm。本文使用的docplex是pip直接下载的免费版本,在求解上有限制,想要安装不受限制的版本可以看: https:// zhuanlan.zhihu.com/p/65 5434273
1.2问题模型
在这一小节,我们会介绍待求解的问题模型,如下所示:
max 2x+3y (1)
s.t. 3x + y ≤ 10 (2)
x + 2y ≤ 12 (3)
x, y ≥ 0 (4)
其中,(1)式是目标函数,求解 2x+3y 的最大值;(2)式是第一个约束条件,表示 3x+y 的值不超过10;(3)式是第二个约束条件,表示 x + 2y 的值不超过12;(4)式是第三个约束条件,表示 x,y 值非负。
2.docplex求解问题
2.1导入包
如果使用pycharm,可以按照如下步骤导入包:
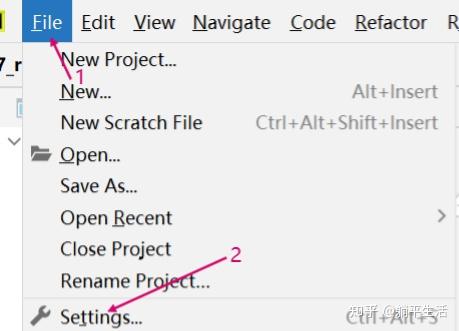

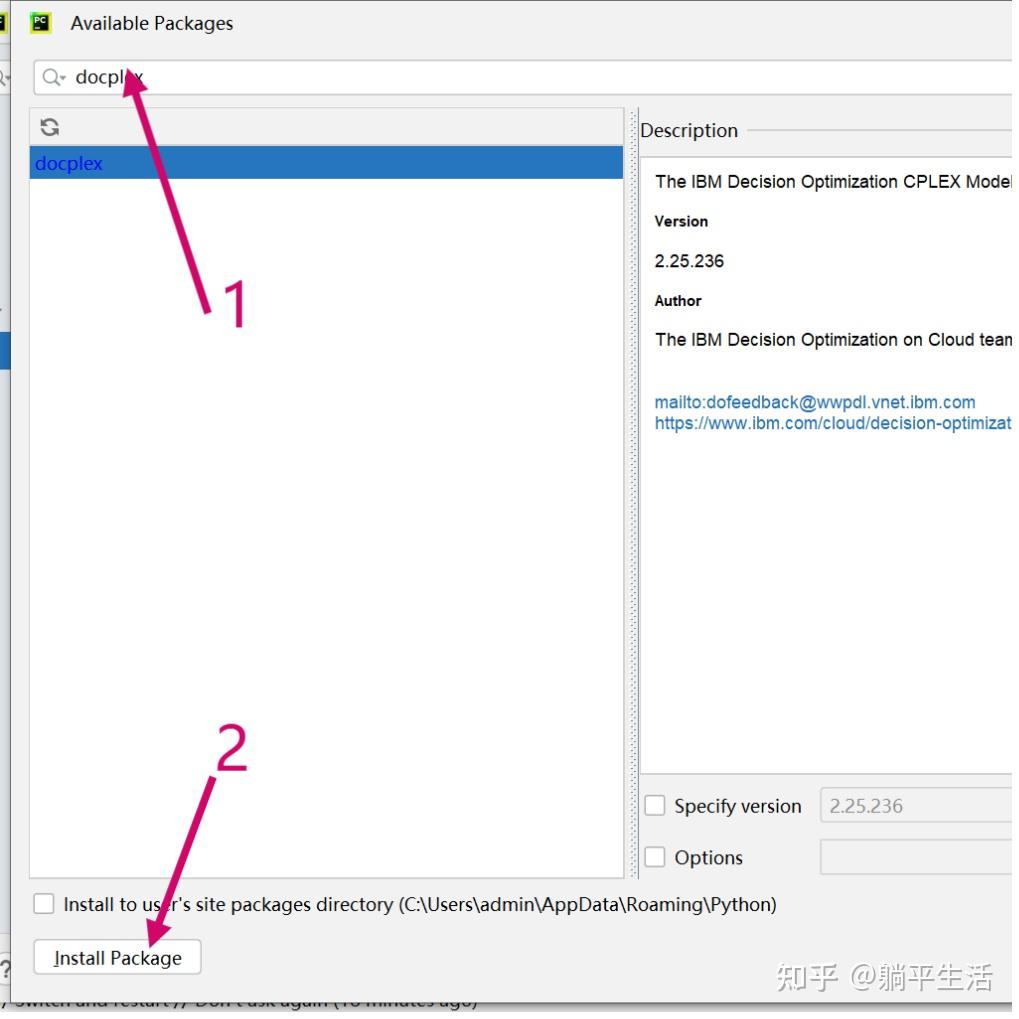
按下install package 后,等待下载完成即可,如果下载失败,可以尝试更换网络,或者在控制台执行如下语句:
pip install docplex安装完成后,使用下面语句,导入docplex包:
from docplex.mp.model import Model2.2定义模型
使用如下语句定义模型:
cplex_obj = Model()其中,cplex_obj为自己定义的变量,符合python变量命名要求即可;Model(),可以有参数name,为模型添加名称。注意:后面使用的cplex_obj均是这里定义的。
2.3添加变量
使用如下语句添加变量:
x = cplex_obj.continuous_var(name='x')
y = cplex_obj.continuous_var(name='y')其中,我们使用定义了x和y两个连续值变量,其默认lb(取值下界)为0,默认ub(取值上界)为infinit(无穷大)。在添加变量时,我们也可以根据需求添加其他变量,例如:
# 定义一个名为tmp的二元变量,取值为0或1
tmp1 = cplex_obj.binary_var(name='tmp')
# 定义一个连续值变量的列表,其中一共有10个元素
tmp2 = cplex_obj.continuous_var_list([i for i in range(10)], name='tmp2')我们在上面举了例子,其中还有一些其他的定义变量的语句,在此不过多赘述。
2.4创建目标函数
使用如下语句创建目标函数:
cplex_obj.maximize(2*x + 3*y)其中,括号内 2x+3y 是待求解的目标函数,目标是最大化这个函数,同样有 cplex\_obj.minimize() 目标是最小化括号内的函数。
2.5添加约束
使用如下语句添加约束:
model.add_constraint(3*x + y <= 10)
model.add_constraint(x + 2*y <= 12)其中,第一句是(2)式的约束;第二句是(3)式的约束。注意,第三个约束在添加变量设置下界时完成,所以只有两个约束。
2.6求解模型
使用如下语句求解模型:
solution = cplex_obj.solve()注意,只需要添加该语句,即可自动完成求解,solution中保存了求解结果,可以 print(solution) 直接查看结果,当然,对于复杂的问题,可能会存在无法求解的情况,我们可以先判断是否求解成功后,再输出结果,如下所示:
solution = cplex_obj.solve()
if solution:
print(solution)
else:
print("求解失败")至此,一个简单的应用docplex求解线性规划问题的教程已经完成,下面是完整代码。
2.7求解代码
完整的求解代码如下:
# 导入docplex
from docplex.mp.model import Model
# 创建模型对象
cplex_obj = Model()
# 添加变量
x = cplex_obj.continuous_var(name='x')
y = cplex_obj.continuous_var(name='y')
# 添加约束
cplex_obj.add_constraint(3*x + y <= 10)
cplex_obj.add_constraint(x + 2*y <= 12)
# 添加目标函数
cplex_obj.maximize(2*x + 3*y)
# 求解优化问题
solution = cplex_obj.solve()
# 获取结果