煤炭资源型城市环境效率及其环境生产率变动分析──基于山西省11个地级市面板数据

link管理

链接快照平台

输入网页链接，自动生成快照
标签化管理网页链接

相关文章推荐

健壮的饭盒 · JSON 路径表达式 - SQL ...· 1 年前 ·

酷酷的小蝌蚪 · mysql输出字符串-掘金· 1 年前 ·

睿智的小蝌蚪 · element ui --- table ...· 2 年前 ·

绅士的牛肉面 · 解决javax.net.ssl.SSLHan ...· 2 年前 ·

鬼畜的帽子 · php - Warning: ...· 2 年前 ·

1. School of Economics and Management, Southwest University of Science and Technology, Mianyang 621010, Sichuan, China

2. Rural Information and Agricultural Economy Research Institute, Sichuan Academy of Agricultural Sciences, Chengdu 610066, China

绿色环境效率反映经济发展与资源环境之间的平衡关系,合理评价资源型城市的环境效率对于促进经济高质量发展具有重要的现实意义。首先从异质性环境污染排放角度出发,选取了四种环境压力指标,采用非径向的Slacks Based Model（SBM）模型和Sequential Malmquist指数模型,对山西省2003—2016年11个地级市的环境效率和环境生产率的区域差异及其动态演进进行了深入分析,然后采用固定效应模型、差分广义矩估计模型和面板分位数回归模型分析了环境规制对山西环境生产率的影响。研究结果表明：（1）在维持现有技术水平不变的前提下,山西省整体的环境效率仍有25.31%的改进潜力;中部地区的环境效率值高于北部与南部地区,但是三大区域的环境效率值都呈下降趋势。（2）山西省环境生产率平均每年提高14.63%,其中技术效率对环境生产率的增长表现为负效应,而技术进步是环境生产率提高的主要来源。（3）环境规制与环境生产率之间并不存在正向或者负向的线性关系,而是存在显著的“U”型关系;不同分位点上环境规制对环境生产率变动的影响表现出明显的异质性。

Green environmental efficiency reflects the balance between economic development and resources environment. It is of great practical significance to evaluate the environmental efficiency of resource-based cities comprehensively for promoting high-quality economic development. From the perspective of heterogeneous environmental pollution emissions, this paper selects four environmental pressure indicators, and uses non-radial SBM model and Sequential Malmquist index model to conduct an in-depth analysis of the regional differences and dynamic evolution of environmental efficiency and environmental productivity of 11 cities in Shanxi Province during 2003-2016. Then it adopts the fixed effect model, differential generalized moment estimation model and panel quantile regression model to analyze the impact of environmental regulation on environmental productivity in Shanxi. The results show that: (1) Under the premise of maintaining the existing technology level, the overall environmental efficiency of the study area still has 25.31% potential for improvement; the environmental efficiency value of the central part is higher than that of the northern and southern parts, but the environmental efficiency values of the three regions are declining. (2) The average annual growth rate of environmental productivity is 14.63%. The increase of technical efficiency to environmental productivity shows a "negative effect", and technological progress is the main source of the increase of environmental productivity. (3) There is no linear relationship between environmental regulation and environmental productivity, but there is a significant "U" type relationship. In different quantiles, the impact of environmental regulation on environmental productivity shows significant heterogeneity.

山西作为我国重要的产煤基地之一,119个县（市、区）中94个有丰富的煤炭资源,探明资源储量约2674亿t,约占全国1/4。自1949年以来,山西省煤炭外调量超过120亿t,占全国外调量2/3以上,这也为中国经济快速发展奠定了坚实的能源基础。但与此同时,经过长期的粗放式开采,山西境内的煤炭资源型城市逐渐出现资源枯竭等问题。2017年山西各城市的采空塌陷面积约3407 km ² ,主要分布在大同、临汾、长治、吕梁、忻州等煤矿开采集中的地区。虽然近年来,大同、阳泉和临汾的环境空气质量有所改善,但是根据 2017年中国生态环境部公布的全国城市环境质量排名,临汾等城市的排名依然位居后列。这不仅给产煤地区的可持续发展带来严峻挑战,更严重制约着山西省的经济转型发展。因此,研究山西省环境效率及其环境生产率的变动,有助于发现煤炭资源型城市转型过程中的优势与弊端,对于提升煤炭资源型城市产业结构优化升级具有重要的现实意义。

“环境效率”最先由世界企业可持续发展协会（WBCSD）提出,在数值上表示为经济单元的经济产出与环境影响的比例,用来反映经济发展与环境保护之间的平衡关系 ^{[

1

]} 。近年来,对环境效率或者生态效率的评价已成为学者们研究的重点。关于环境效率的测算常用的方法有数据包络分析方法（DEA）、生态足迹法（Ecological Footprint）以及IPAT模型等。如,王兆峰等 ^{[

2

]} 采用非期望产出的SBM模型测算了长江经济带旅游生态效率。史丹等 ^{[

3

]} 以单位生态足迹的GDP产出来表征生态效率,对中国1991—2013年的生态效率变动进行了分析。罗能生等 ^{[

4

]} 采用超效率DEA和IPAT模型分析了城镇化率与区域生态效率之间的关系。由于DEA方法是一种非参数方法,不需要主观设定权重,且无需要对数据进行量纲处理,因而在环境效率评价方面得到了广泛的应用 ^{[

5

]} 。为了使用DEA方法来对环境效率进行合理评价,一些学者从不同角度进行了有益尝试。现有文献对污染排放量的处理方法主要分为三类：一是将污染排放变量作为投入要素引入 ^{[

6

,

7

,

8

]} 。例如,Kuosmanen等 ^{[

6

]} 首次提出在DEA框架下测算环境效率,他们从生态经济学角度,以环境压力指标来取代污染产出指标,利用帕累托最优思想来测算最优的环境效率。国内一些学者在Kuosmanen模型基础上对中国环境效率或生态效率进行了测算分析 ^{[

9

,

10

]} 。例如,杨文举 ^{[

9

]} 在借鉴Timmer等 ^{[

8

]} 模型基础上,研究发现中国区域工业环境效率普遍偏低且差异较大;汪克亮等 ^{[

10

]} 将生态压力指标纳入到DEA分析框架中测算了2006—2015年的中国省际生态效率,研究发现技术进步是驱动生态效率提升的主导因素。二是对污染排放量做处理后作为期望产出 ^{[

11

,

12

]} ,即把非期望产出（污染排放量）的值进行倒数变换。但是该方法有一定的缺陷,与实际生产过程存在偏差。三是将污染排放量作为有弱可处置性的非期望产出,与期望产出一起引入,利用方向性距离函数来进行测算 ^{[

13

]} 。该方法可以较好地评价环境效率,但是这类模型不能充分考虑到投入产出的松弛性问题,导致其在环境效率评价中存在识别不够好的缺陷。为此,Tone ^{[

14

]} 提出了解决这一问题的非径向Slacks Based Model（SBM）模型,它可以有效避免径向和角度选择带来的偏差。李占风等 ^{[

15

]} 通过构建环境污染综合指数代表非期望产出,采用Undesirable SBM模型测算了中国30个省市工业环境效率。黄建欢等 ^{[

16

]} 采用共同前沿技术和Undesirable SBM模型测算了中国191个地级市的生态效率。由于近年来中国环境治理问题再次引起学术界关注,而目前将DEA方法运用到资源型城市环境效率评价的研究还有待进一步深入探究。其中具有代表性的文献,如白雪洁等 ^{[

17

]} 采用非期望产出的动态SBM模型对中国2005—2012年资源衰退城市的经济效率进行了测算,发现资源衰退城市的节能减排效果与政府的政策力度呈现较高的一致性。肖滢等 ^{[

18

]} 采用全局SBM Malmquist模型从静态和动态对我国资源型城市的绿色工业经济效率进行了测度,发现资源型城市的绿色经济效率整体偏低,但呈现出逐渐改善的趋势。

综上所述,现有研究还存在一些不足之处：第一,以往文献在衡量环境效率时大多采用单要素指标,如CO ₂ 排放强度、SO ₂ 排放强度等指标,这些指标计算简易、便于理解,但是忽视了经济系统在生产过程中会排放多种环境污染物的情况,而且也无法反映不同污染排放物之间的相互替代关系,从而使得测算结果并不准确。第二,以往研究测算环境效率时基本都是在传统的全要素框架下加入资本、劳动和能源等生产要素作为投入来进行测算,这样测算出来的效率既可称为资本效率,也可称为劳动效率或者能源效率。本文的边际贡献主要有：（1）从异质性环境污染排放角度出发,选取四种环境污染排放物来衡量“环境压力”指标。与传统指标的区别在于,环境效率测算公式中的分母并不是一种环境污染排放物,而是将多种“环境压力”指标综合至同一指标之中,给予每个“环境压力”指标赋予一定的权重,并且该权重值不是主观设定,而是采用非参数法客观计算得来。（2）对Kuosmanen模型做进一步扩展,将非径向的SBM模型和Sequential Malmquist指数模型引入到模型中,目的是以解决松弛变量的非径向问题和技术可能存在的“退步”问题。因此,根据世界企业可持续发展协会对环境效率的定义,将环境污染排放视为“环境压力”,采用非径向的SBM模型和Sequential Malmquist模型来测算2003—2016年山西省的环境效率及其环境生产率变动的区域差异和演变特征,以期为资源型城市的转型发展提供具有针对性的对策建议。

（1）

\begin{array}{l} \min θ^{*} = \frac{1 - \frac{1}{m} \overset{m}{\sum_{i = 1}} s_{i}^{-} / x_{i 0}}{1 + \frac{1}{r} \overset{r}{\sum_{i = 1}} s_{i}^{-} / y_{i 0}} \\ s.t. x_{i 0} = \overset{n}{\sum_{j = 1}} x_{ij} λ_{j} + s_{i}^{-} (i = 1, \dots, m) \\ y_{r 0} = \overset{n}{\sum_{j = 1}} y_{rj} λ_{j} - s_{r}^{+} (r = 1, \dots, s) \\ λ_{j} \geq 0 (\forall_{j}), s_{i}^{-} \geq 0 (\forall_{i}), s_{r}^{+} \geq 0 (\forall_{r}) \end{array}

式中：

x_{ij}

表示第

j

个决策单元的第

i

个投入变量;

y_{rj}

表示第

j

个决策单元的第

r

个产出变量;

λ_{j}

表示参照集中各要素的权重;

s^{-}

和

s^{+}

分别表示投入过剩和产出不足的松弛变量。如果DMU是有效的,那么模型的最优解

θ^{*} = 1

,则此时的

s^{-} = 0

s^{+} = 0

。SBM模型与传统的径向DEA模型不同之处在于把松弛变量引入到了目标函数中。

（3）

\begin{array}{l} MI = \sqrt[]{\frac{D_{i}^{t} (x^{t + 1}, y^{t + 1})}{D_{i}^{t} (x^{t}, y^{t})} \frac{D_{i}^{t + 1} (x^{t + 1}, y^{t + 1})}{D_{i}^{t + 1} (x^{t}, y^{t})}} \\ = \frac{D_{i}^{t + 1} (x^{t + 1}, y^{t + 1})}{D_{i}^{t} (x^{t}, y^{t})} \times \sqrt[]{\frac{D_{i}^{t} (x^{t + 1}, y^{t + 1})}{D_{i}^{t + 1} (x^{t + 1}, y^{t + 1})} \frac{D_{i}^{t} (x^{t}, y^{t})}{D_{i}^{t + 1} (x^{t}, y^{t})}} = TEC \times TC \end{array}

山西省作为煤炭资源型大省的代表,同时也是我国资源型城市最多的省份。因此,研究对象选取了2003—2016年山西省11个地级市的面板数据。为了体现资源禀赋与地理位置的差异,本文将山西省11个地级市分为北部地区（大同、朔州和忻州）、中部地区（太原、阳泉、吕梁和晋中）和南部地区（长治、临汾、运城和晋城）。借鉴Kuosmanen等 ^{[

6

]} 的做法,将环境效率定义为经济产出与环境压力的比值。其中“环境压力”是决策单元在生产过程中的环境污染排放,需要指出的是环境污染排放作为投入,类似生态形式的社会资本的投入和使用 ^{[

22

]} 。这里虽然没有考虑到常规投入（资本和劳动力）对环境效率的影响,有一定的局限性,但是该方法的测算结果在某种程度上更能准确地反映环境保护与经济发展之间的协调关系 ^{[

23

]} 。具体来说,将“环境压力”作为投入变量,经济产出作为产出变量,构造一个“环境技术集合”,以此反映决策单元在经济产出增长的同时,污染排放物所能够减少的技术水平和能力 ^{[

24

]} 。其中,投入变量为2003—2016年山西省11个地级市的工业二氧化硫排放量、工业烟尘排放量、工业废水排放量与PM _2.5 浓度。产出变量为2003—2016年山西省11个地级市的地区生产总值与煤炭产量。另外,与传统的单一维度指标的主要区别在于,环境效率计算公式中的分母并不是某一种环境污染排放物,而是一种综合指标,该指标给予每个“环境压力”指标赋予不同的权重,并且该权重是采用非参数法客观计算而来,不需要事前主观人为设定。

表1 主要指标的统计性描述

Table 1 Statistical description of main indicators

变量	观测值	均值	Std. Dev.	最小值	最大值
地区生产总值/万元	154	4637772.00	2741752.00	1093822.00	15300000.00
煤炭产量/万t	154	6451.01	4158.22	28.00	22091.00
工业二氧化碳/t	154	95439.75	28360.69	14328.00	183656.00
工业烟尘/t	154	127149.10	483326.00	15163.00	5168812.00
工业废水/万t	154	3601.03	2301.18	458.00	14365.00
PM _2.5 /(μg/m ³ )	154	27.74	6.69	15.52	51.11

表2 2003—2016年山西省环境效率值

Table 2 Environmental efficiency values in Shanxi province from 2003 to 2016

地区/年份	2003	2004	2005	2006	2007	2008	2009	2010	2011	2012	2013	2014	2015	2016	平均
大同	1.0000	1.0000	0.9695	0.8631	1.0000	0.6240	0.6068	1.0000	0.5749	0.5322	0.5480	0.6380	0.6524	1.0000	0.7617
朔州	0.4696	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	0.9474
忻州	0.7641	1.0000	0.4885	0.4995	0.4732	0.3566	0.3439	0.4858	0.3572	0.3797	0.3881	0.3852	0.3509	0.3520	0.4481
北部平均	0.7106	1.0000	0.7795	0.7554	0.7793	0.6060	0.5931	0.7861	0.5900	0.5869	0.5969	0.6264	0.6117	0.7061	0.6864
太原	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000
阳泉	1.0000	1.0000	1.0000	0.7977	0.8401	1.0000	1.0000	0.6190	0.7952	1.0000	1.0000	1.0000	1.0000	1.0000	0.9238
吕梁	1.0000	1.0000	1.0000	1.0000	0.7299	0.5752	0.5563	1.0000	1.0000	1.0000	0.4856	0.4762	0.4292	0.3913	0.7147
晋中	1.0000	1.0000	1.0000	0.8342	1.0000	0.6842	0.6679	0.5953	0.4852	0.4704	0.4092	0.5716	0.5318	0.7764	0.6850
中部平均	1.0000	1.0000	1.0000	0.9032	0.8849	0.7921	0.7807	0.7791	0.7881	0.8282	0.6677	0.7223	0.6912	0.7424	0.8201
长治	1.0000	1.0000	0.7739	0.7575	0.7986	0.7431	0.7047	0.6109	0.4897	0.4644	0.4714	0.5219	0.5319	0.5581	0.6516
临汾	1.0000	1.0000	1.0000	1.0000	0.8800	0.6036	0.5538	0.6667	0.5409	0.4095	0.4990	0.5645	0.5252	0.5933	0.6718
运城	0.6082	0.8281	0.5288	0.4231	0.4094	0.4186	0.4273	0.3852	0.4912	0.4563	0.4544	0.3802	0.3362	0.4296	0.4578
晋城	1.0000	1.0000	1.0000	1.0000	0.9248	1.0000	1.0000	0.5578	0.5325	0.4937	0.4786	0.5364	0.5006	0.3312	0.6920
南部平均	0.8831	0.9540	0.7998	0.7524	0.7182	0.6582	0.6390	0.5439	0.5131	0.4549	0.4756	0.4951	0.4657	0.4659	0.6102
平均	0.8708	0.9830	0.8614	0.8050	0.7923	0.6884	0.6735	0.6854	0.6230	0.6063	0.5724	0.6056	0.5791	0.6182	0.7016

从三大地区来看,山西北部、中部与南部的环境效率均值分别为0.7003、0.7471和0.6598,呈现出自北向南的低—高—低的趋势,中部地区最高,其次是北部地区,最后是南部地区,这在一定程度上说明地区的环境效率值与经济发展水平呈正相关。山西中部地区有太原市,地理位置相对优越,交通基础设施较为完善,开放性水平较高,外资吸引能力明显高于北部与南部地区。而大量外资可为中部地区城市带来更多的先进技术和管理理念。与此同时,中部地区煤炭资源相对偏少,这就促进了中部地区的城市产业结构不断优化,使得中部地区的环境效率相对北部和南部地区来说要高。山西北部地区与南部地区拥有充裕的煤炭资源,1949年以来对外输出大量的煤炭资源,另外这些地区的城市自身交通基础设施建设滞后,无法有效吸引外部投资,持续依靠煤炭资源作为经济发展的主动脉,使得经济发展动力不足,同时在生产煤炭的过程中产生了大量的环境污染物,这些都是导致北部与南部地区环境效率值较低的原因。

从单个地级市来看（图1 ）,2003—2016年间太原一直处在生产前沿上,环境效率值为1,这主要是太原具有明显的地理区位优势和经济发展优势,再加上太原陆续出台了一系列的生态环境保护的法律和政策,如2008年太原就制定了《太原市绿色转型促进条例》;2016年太原印发了《太原市水污染防治行动计划》;2018年又出台了全国首部地区性生态环境保护条例《太原市生态环境保护条例》。环境效率均值在0.75以上的还有朔州、大同、阳泉,说明这些城市在处理经济发展与资源环境方面还相对较为协调,比如2016年大同的煤炭产量达到9560万t,在山西省各城市中排名第四。与此同时,大同不断加快从“煤都”向“氢都”和“新能源之都”转变,环境质量也在不断改善,2016年大同空气质量综合指数为5.21,在全省排名第一。排名靠后的忻州与运城,环境效率值在0.5以下,这可能由于这些城市的产业结构落后导致的环境效率低下,比如忻州和运城的产业升级指标（这里采用第三产业增加值与第二产业增加值的比值来表示）分别从 2004年的1.14、2.29下降到2016年的0.94、0.97,这也间接说明这两个城市的产业结构转型升级还任重道远。

从时间变化趋势来看（图2 ）,2003—2016年山西省全省与中南部的环境效率值不仅没有改善,并且有下降趋势。其中,全省环境效率值从2003年的0.8708下降到2016年的0.6182,中部地区环境效率值从2003年的1下降到 2016年的0.7424,南部地区从2003年的0.8831下降到2016年的0.4659,北部地区从2004年的1下降到2016年的0.7061。山西环境效率逐年下降的原因可能是：煤炭产业是山西经济发展的支柱产业与主导产业,煤焦、冶金、化工、电力等高能耗产业使得环境污染物排放不断增加。另外,面对国际和国内经济形势的不利影响,山西的经济不断下行,尤其是在2012年后出现了断崖式下滑,全省经济增速由2012年的10.2%下降到2015年的3.1%,另外,山西资源型产业结构问题非常突出,2005—2016年煤炭开采和洗选业增加值占工业增加值比例由38.4%增加到48.32%,这也导致了山西省产业结构严重失衡,从而导致全省的环境效率不断下降。这也表明山西省这种依靠资源消耗与环境污染驱动经济增长的粗放型增长模式并未得到根本转变,实现经济结构转型发展依然是当前和今后一段时间经济社会发展所面临的主要矛盾。

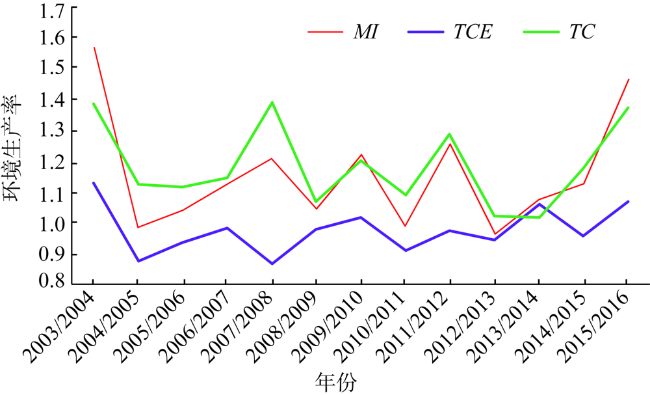
下面采用SBM-时序Malmquist生产率指数模型将环境生产率变动指数分解为技术效率变动指数与技术进步指数。在2003—2016年间,山西环境生产率变动指数平均每年提高14.63%,说明山西整体的环境生产率呈改善趋势（表3 ）。从指数分解结果来看, TEC 平均值为0.9740,年均下降2.6%, TC 平均值为1.1769,年均增长17.69%,这意味着技术效率指数对环境生产率变动影响表现为“负效应”,技术进步指数对环境生产率变动的影响表现为“正效应”（图4 ）,由于这种“正效应”的作用大于“负效应”,最终使得山西环境生产率整体上还是表现为改善状态,即技术进步是山西环境生产率提高的主要来源。

表3 2003—2016年山西省年环境生产率变动

Table 3 Changes in environmental productivity in Shanxi province from 2003 to 2016

地区/年份	2004	2005	2006	2007	2008	2009	2010	2011	2012	2013	2014	2015	2016	平均
大同	1.3385	0.9882	0.8947	1.3046	1.0224	1.0150	1.8516	0.7760	1.1218	1.0409	1.1643	1.1722	2.0924	1.1698
朔州	3.1672	1.0116	1.1570	1.2872	1.2938	1.1311	1.2297	1.0711	1.3120	1.0191	1.0110	1.0821	1.3036	1.2465
忻州	1.8818	0.5011	1.0662	1.1100	0.9443	1.0231	1.6725	0.7855	1.2835	1.0225	1.0154	1.0396	1.2496	1.0714
北部平均	1.9981	0.7942	1.0335	1.2307	1.0770	1.0551	1.5616	0.8675	1.2362	1.0274	1.0612	1.0966	1.5049	1.1603
太原	1.3895	1.1063	1.1014	1.1175	1.2587	1.0367	1.1390	1.0321	1.0629	1.0568	1.0425	1.3223	1.4393	1.1544
阳泉	1.5602	1.0103	0.9865	1.2788	1.7479	1.0486	0.6732	1.3858	1.6253	1.0095	1.0050	1.0632	1.0239	1.1493
吕梁	1.3209	1.1517	1.2431	0.8085	1.0479	1.0255	2.0356	1.0290	2.1417	0.4856	0.9913	0.9740	1.1552	1.1124
晋中	1.3081	1.0877	0.8471	1.3741	1.0048	1.0602	1.0415	0.8781	1.1261	0.8728	1.4244	1.0913	2.0361	1.1321
中部平均	1.3912	1.0878	1.0342	1.1225	1.2337	1.0427	1.1291	1.0662	1.4287	0.8200	1.1029	1.1056	1.3645	1.1369
长治	1.3610	0.8078	1.0398	1.2409	1.2880	0.9917	1.0284	0.8646	1.1367	1.0237	1.1443	1.1952	1.7013	1.1200
临汾	1.3104	1.2680	1.2273	0.9425	1.1342	0.9298	1.5774	0.8488	0.8760	1.2548	1.1449	1.1826	1.8833	1.1689
运城	1.7468	1.1481	0.9504	1.1001	1.2791	1.0814	1.0412	1.2757	1.0399	1.041	0.8435	1.1572	1.8372	1.1674
晋城	1.4772	1.0142	1.0314	0.9679	1.4759	1.1832	0.8589	1.1444	1.4607	1.0055	1.1231	1.1410	0.9640	1.1256
南部平均	1.4647	1.0450	1.0576	1.0564	1.2887	1.0422	1.0975	1.0174	1.1090	1.0768	1.0555	1.1688	1.5434	1.1453
平均	1.5646	0.9839	1.0424	1.1259	1.2078	1.0459	1.2209	0.9909	1.2525	0.9629	1.0741	1.1257	1.4657	1.1463

显示原图 | 下载原图ZIP | 生成PPT

图4 2003—2016年山西省环境生产率变动及其分解指数的变化

Fig. 4 Changes in environmental productivity and its decomposition index in Shanxi province from 2003 to 2016

从动态视角来看,山西在2003—2004年环境生产率变动指数增幅达56.46%,而2004—2005年却下降2.61%;2009—2010年环境生产率变动指数上升22.09%,而2010—2011年有0.91%的小幅度下降,这有可能与2010年山西设立“综改区”政策调整有关。而到了2015—2016年环境生产率又出现大幅上升的态势（图5 ）,这可能与山西省近年来的能源政策和环境政策有很大关系,比如2015—2016年山西省先后发布了《山西省应对气候变化规划（2015—2020）》《山西省环境保护“十三五”规划》《山西省煤炭供给侧结构性改革实施意见》《山西省国家资源型经济转型综合配套改革试验实施方案》。

从单个地级市来看（表3 ）,2003—2016年间山西各地级市环境生产率变动指数均呈增长状态,有6个地级市超过全省平均水平,说明山西城市转型的资源配置水平虽然较低,但仍处于缓慢增长状态。根据指数分解结果,只有朔州技术效率增长5.99%,大同、太原、阳泉均无变化,运城与临汾分别下降2.64%与3.94%,均在山西技术效率变动均值以下;临汾技术进步有21.68%的增长,大同有19.9%的增长,其他4个地级市技术进步虽有增长但均在山西平均水平之下。晋中、晋城、长治、吕梁与忻州环境生产率变动指数在山西平均水平之下,这5个地级市技术效率水平均有不同程度下降,但技术进步“正效应”抵消了技术进步“负效应”。

从三大地区来看,2003—2016年间山西三大地区的环境生产率变动指数均呈增长状态,年均分别增长16.03%、13.69%和14.53%,其中北部地区增速最快,南部地区次之,中部地区增速最慢。根据指数分解结果,三大地区的技术效率在研究期内都是下降的,年均分别下降0.05%、2.27%和4.8%,三大地区的技术进步指数均上升,年均增长16.09%、16.33%和20.3%（图6 ）。技术效率不断下降的原因一方面可能由于山西省各地市政府的资源环境管理水平相对较低;另一方面可能由于地方官员受到政绩和经济利益的驱使,没有严格执行国家的资源环境保护政策。技术进步不断提高的原因可能来自于山西省近年来不断加快实施《山西打造全国能源革命排头兵行动方案》,通过突破能源核心技术、推广节能产业工程,从而不断提高山西绿色转型中的技术进步。

关于环境规制与生产率的关系,学术界尚存一定争议。目前主要有三种观点：第一种观点认为环境规制阻碍了生产率的提高。该观点认为严格的环境规制会增加国内企业的污染治理成本,抑制企业研发创新活动,进而降低企业生产率 ^{[

25

,

26

]} 。第二种观点认为环境规制促进了生产率的提高。该观点认为合理的环境规制可以促进企业进行技术创新,从而抵消企业的环境治理成本,进而提升企业生产率 ^{[

27

,

28

]} 。第三种观点认为环境规制与生产率之间存在非线性关系,如陈菁泉等 ^{[

29

]} 研究发现环境规制强度与环境全要素生产率呈“U型”关系;王杰等 ^{[

30

]} 研究发现环境规制与企业全要素生产率之间呈“倒N型”关系。那么,最为典型的煤炭资源型省份——山西省,环境规制与环境生产率之间是一种什么关系呢?这需要我们进一步深入研究。因此,本文采用2003—2016年山西省各地级市数据,利用面板数据模型研究环境规制与环境生产率之间的关系。计量模型设定如下：

计量模型中变量选取和衡量方法说明如下：（1）被解释变量：环境生产率变化（ MI ）。以SBM-时序Malmquist模型测算结果来表示。（2）核心解释变量：环境规制（ ER ）。选取城市生活污水、固体废弃物和二氧化硫去除率作为度量各城市环境规制强度指标。借鉴董直庆等 ^{[

31

]} 计算单位经济产出排放综合指标的方法,首先将三类污染去除率进行标准化处理,然后采用熵值法确定权重,最后根据标准化数据和权重计算环境规制的总和指标。该指标值越大,表明环境规制强度越大。（3）主要控制变量：一是资源禀赋（ endow ）,采用采矿业就业人员与就业人员之比来衡量 ^{[

32

]} 。二是基础设施建设水平（ trans ）,选取人均货运总量来表示。三是外商直接投资（ fdi ）,采用外商投资工业企业总产值占该地区工业总产值的比例表示。四是经济发展水平（ agdp ）,采用人均GDP反映一个城市的经济发展水平。五是财政干预度（ gov ）,选取财政预算内支出占财政预算内收入的比例。六是产业结构比例（ indus ）,选取第二产业产值占该城市GDP的比例来表示。七是人口密度（ pd ）,选取各地级市年末人口数与全市行政区域面积之比。八是就业结构（ emstr ）,选择第三产业就业占年末就业总人口比例来表示。九是金融发展规模（ fin ）,采用金融机构各项贷款和存款之和来表示。数据主要来源于《山西省统计年鉴》《中国城市统计年鉴》和《中国环境统计年鉴》,并以2003年为基期换算为可比价。各指标统计性描述如表4 所示。

表4 主要变量的统计性描述

Table 4 Statistical description of main variables

变量	观测值	均值	Std. Dev.	最小值	最大值
MI	143	1.184	0.332	0.486	3.167
ER	143	1.090	1.567	0.017	8.197
agdp	143	17174.45	8170.548	4199.384	45410.11
endow	143	0.17	0.177	0	0.516
emstr	143	55.023	16.179	27.24	91.26
trans	143	43.932	28.919	6.904	142.042
fdi	143	0.036	0.035	0.001	0.154
gov	143	0.389	0.753	0.08	4.035
pd	143	282.09	132.426	24.42	531.02
fin	143	0.179	0.349	0.007	2.043
indus	143	54.739	8.53	36.12	73.71

表5 基本回归结果

Table 5 Basic regression results

变量	(1)	(2)	(3)	(4)	(5)
ER	0.129 ^**	-0.236 ^**	-0.218 ^*	-0.209 ^**	-0.273
	(2.035)	(-2.599)	(-2.021)	(-2.312)	(-1.382)
ER 2	—	0.0430 ^***	0.0423 ^***	0.0350 ^***	0.0415 ^***
	—	(6.537)	(6.087)	(4.869)	(3.253)
ln agdp	-0.433	-0.215	-1.153	1.645	2.444
	(-1.221)	(-0.625)	(-0.749)	(1.617)	(0.652)
ln agdp 2	—	—	0.0500	-0.105 ^*	-0.136
	—	—	(0.599)	(-1.837)	(-0.855)
endow	1.170 ^*	1.423 ^**	1.423 ^***	1.095 ^**	1.208
	(1.911)	(3.126)	(3.227)	(2.446)	(1.631)
emstr	0.00811 ^*	0.00881 ^***	0.00917 ^***	0.00671 ^**	0.0139 ^*
	(1.877)	(4.884)	(4.216)	(3.121)	(2.022)
trans	0.00182	0.00133	0.00154	0.00331 ^***	0.00385 ^***
	(1.144)	(1.369)	(1.450)	(3.526)	(3.152)
fdi	-0.360	-0.500	-0.605	-1.013	-3.656
	(-0.318)	(-0.432)	(-0.493)	(-0.881)	(-1.241)
gov	-0.494 ^***	-0.692 ^***	-0.690 ^***	-0.717 ^***	-0.859 ^***
	(-3.129)	(-8.321)	(-8.388)	(-9.352)	(-3.880)
ln pd	-2.353 ^**	-1.738 ^***	-1.842 ^***	-0.926	-1.059
	(-2.012)	(-3.945)	(-4.124)	(-1.304)	(-0.997)
ln fin	0.252	0.187	0.175	0.249	0.343
	(1.179)	(0.938)	(0.832)	(1.140)	(0.773)
indus	-0.0120 ^**	-0.0114 ^*	-0.0106 ^*	-0.00556	-0.0199
	(-2.185)	(-2.057)	(-1.954)	(-0.709)	(-1.102)
L.ln MI	—	—	—	-0.263 ^***	-0.197 ^**
	—	—	—	(-3.699)	(-2.302)
城市效应	—	—	—	控制	控制
时间效应	—	—	—	控制	控制
观测值	143	143	143	132	121

注：1. ^* 、 ^** 、 ^*** 分别表示在10%、5%、1%的水平下显著,下同。2. 为了尽可能减少异方差的影响, MI 、 agdp 、 pd 和 fin 都取了对数。3. 在回归分析时使用的是聚类稳健标准误。4.“—”表示没有控制该变量。

首先运用个体固定效应模型（模型1）探究环境规制对山西省环境生产率的影响。回归结果显示,环境规制对环境生产率的影响系数为0.129,在5%的水平下显著,说明在全省层面环境规制对生产率存在显著的促进作用。但是模型1并没有考虑环境规制与生产率之间可能存在的非线性关系,因此在模型2中加入了环境规制的平方项,可以看出环境规制的一次项和平方项估计系数分别显著为负和正,说明环境规制与生产率之间存在“U型”关系,这与Wang等 ^{[

33

]} 、杜龙政等 ^{[

34

]} 的研究结论一致。同时考虑到经济发展与环境生产率之间可能存在非线性关系,因此本文在模型2的基础上又加入了人均GDP的平方项,从模型3可以看出环境规制与生产率之间的关系依然是“U型”关系。虽然模型1~模型3控制了不同城市之间的差异,但并未控制随时间变化的因素对回归结果造成的影响。同时考虑到城市环境质量也会影响一个城市采取何种强度的环境规制水平,使得环境规制与环境生产率存在双向因果关系。因此,本文在模型1~模型3的基础上加入环境生产率的时间固定效应和滞后项,可以看出结果依然保持一定的稳健性。为了尽可能减少内生性问题,采用动态差分GMM模型来进行估计。从模型5可以看出环境规制的平方项的估计系数依然在1%的显著水平下为正,说明环境规制与环境生产率之间呈现“U型”关系。在政府的环境规制强度较低时,企业可能会选择投入更多的资金来扩大再生产,购置新设备导致对研发创新产生了“挤出效应”,从而导致环境生产率的下降。另外,地方政府可能为了短期的经济增长而放松对企业的环境规制,从而不利于城市的要素结构优化和产业结构升级,最终抑制了山西环境生产率的提高。随着环境规制强度的提高,当超过“U型”曲线的拐点后,政府的环境规制使得企业的环境治理成本不断增加,企业为了在市场竞争中生存下来,不得不进行新的清洁技术的研发或者改进已有的生产工艺,从而企业的环境排污会不断减少,最终使得环境生产率不断得到改善。

由于不同城市在经济发展水平、资源禀赋等方面存在差距,在条件分布不同时,传统的最小二乘估计方法不能体现出环境规制对环境生产率的异质性影响。因此,采用Powell ^{[

35

]} 提出的非可加性固定效应的面板分位数回归模型（QRPD）。相比传统可加性面板分位数回归模型,该模型保留了与分位数估计相关的不可分扰动项,能够很好地克服传统分位数回归模型产生的估计偏差问题。由表6 的面板分位数回归模型可以看出,环境规制平方项的回归系数符合与表5 的模型结果一致,只在不同分位点处表现明显的异质性,进一步印证了上述结论的稳健性,说明了政府在制定环境政策时要因地制宜。对于较高分位点的城市,不要盲目提高环境规制力度,而应完善现有环境保护法规体系,提高自身环境治理能力和管理效率。而处于低分位点的城市,政府部门应适度提高环境规制力度,激励企业进行绿色技术或工艺的改造升级,努力提高地方经济的增长质量。

表6 面板分位数模型回归结果

Table 6 Regression results of panel quantile model

变量	(1)	(2)	(3)	(4)	(5)
ER	0.132 ^***	-0.0642 ^***	-0.0333	-0.172 ^***	-0.0400
	(203.8)	(-12.51)	(-0.793)	(-4.139)	(-0.873)
ER 2	0.00163 ^***	0.0132 ^***	0.00766 ^*	0.0342 ^***	0.0312 ^***
	(26.99)	(19.06)	(1.733)	(7.104)	(5.241)
ln agdp	0.312 ^***	0.655 ^***	-3.145 ^***	-6.130 ^***	-3.007 ^***
	(148.8)	(5.223)	(-5.725)	(-5.067)	(-4.625)
ln agdp 2	-0.0243 ^***	-0.0334 ^***	0.163 ^***	0.315 ^***	0.156 ^***
	(-232.1)	(-4.995)	(6.236)	(4.893)	(4.736)
endow	-0.226 ^***	-0.0123	0.319 ^***	0.527 ^***	0.646 ^***
	(-127.1)	(-0.644)	(3.345)	(4.761)	(8.241)
emstr	0.00108 ^***	0.00156 ^***	0.00356 ^***	0.00607 ^***	0.00689 ^***
	(125.4)	(3.994)	(5.121)	(4.358)	(4.386)
trans	-0.000249 ^***	4.95e-05	0.000644	-0.000525 ^*	-0.00166 ^**
	(-28.18)	(0.686)	(1.022)	(-1.834)	(-2.094)
fdi	-0.474 ^***	-0.119	-1.106 ^***	-0.390	-0.657 ^***
	(-198.3)	(-1.484)	(-3.909)	(-1.057)	(-3.425)
gov	-0.671 ^***	-0.123 ^***	-0.120 ^***	-0.322 ^***	-0.622 ^***
	(-2,899)	(-10.73)	(-10.81)	(-12.12)	(-19.82)
ln pd	-0.281 ^***	-0.0668 ^***	-0.0430 ^*	-0.0816 ^***	-0.236 ^***
	(-383.9)	(-8.127)	(-1.668)	(-3.187)	(-10.43)
ln fin	0.0851 ^***	0.0264 ^***	0.0393 ^*	0.0259	-0.0545 ^**
	(372.4)	(5.316)	(1.883)	(1.510)	(-2.207)
indus	-0.00428 ^***	-0.00253 ^***	0.00384 ^***	0.00463 ^***	-0.0103 ^***
	(-175.1)	(-8.926)	(2.520)	(2.595)	(-5.591)
观测值	143	143	143	143	143

本文首先运用SBM-Sequential Malmquist模型研究山西省内不同城市的环境效率及其差异与环境生产率的动态演变特征,然后采用面板数据模型和面板分位数回归模型分析了环境规制与环境生产之间的因果关系。主要结论如下：（1）山西省全省的环境效率水平较低,仍有25.31%的改进潜力;环境效率值在2003—2016年呈下降趋势。（2）山西省全省环境生产率平均每年提高14.63%,表明山西省环境生产率水平虽然较低,但处于缓慢增长的状态。其中,技术效率的下降是阻碍环境生产率提高的主要原因。（3）环境规制与山西省环境生产率之间存在显著的“U型”关系,表明环境规制对山西省环境生产率的影响并非为线性关系,在一定临界值下环境规制对环境生产率的增长具有负向抑制作用,超过临界值后会对环境生产率具有促进作用。基于以上分析,本文提出如下对策建议：（1）立足煤炭资源优势,推动产业转型升级。重点推进阳泉、晋城、朔州、大同的煤炭产业转型发展,以市场为导向,加快煤炭资源的整合力度,推进企业兼并重组,淘汰落后产能。同时,延伸“煤—焦—化”“煤—电—化”等新兴产业链的发展,利用高新技术改造煤炭产业,提高煤炭企业的核心竞争力。另外,加大忻州地区以及吕梁北部地区的风能开发利用,降低这些城市的单位GDP能耗,推动当地资源经济转型发展。（2）加大区域协同发展,完善环境保护联防机制。一方面山西省各地市要加强区域经济合作,积极发挥太原都市圈经济的影响力,加强对忻州、吕梁和晋中等地的辐射作用。同时,各地区要加强科技、环境等领域的合作,加强各地区大气污染的联防联控机制,从单因子治理向多污染因子综合治理转变,联合推进二氧化硫、氮氧化物、颗粒物等的协同控制,全面推动建设资源节约型与环境友好型的“美丽山西”。（3）对实施适度的政府环境规制强度,不断提升环境生产率。由于山西各资源城市的环境规制环境生产率存在一定的差异性。因此,各地方政府应结合城市的资源禀赋和环境承受能力,制定差异化的环境经济政策体系。同时,要根据现有环境规制强度的作用效果,不断优化各种政策工具,提高资源投入要素的利用效率,实现资源型城市环境生产率的持续提升。（4）坚守生态红线,完善资源环境保护制度。坚持“谁污染谁付费,谁破坏谁补偿”的原则,重点加大对大同、阳泉和临汾的矿产资源的生态保护和修复治理力度;加强对汾河、黄河流域的运城、晋城、临汾等地区的水质监测和污染防治,降低这些城市的工业废水排放强度。同时,山西省应当制定更为严格的生态环境保护法律和法规,划定生态保护红线,合理开发煤炭矿产资源,提高资源利用效率,努力把生态建设作为山西转型综合改革试验区建设的重中之重。

WANG

, SUN

, WANG

, et al. Going green or going away? A spatial empirical examination of the relationship between environmental regulations, biased technological progress, and green total factor productivity. International Journal of Environmental Research and Public Health , 2018 , 15 (9):1917.