时间反演对称（TRS）保护下拓扑绝缘体（二）：如何理解“破坏”&“保护”

在前文中我提到了两个问题：“ 为什么会出现 \times 形状的能带？以及为何这条带对应边缘态？” \times 形状能带和边缘态之所以相当重要，重要原因在于其是稳定的，也就是常说“被对称性”保护的。如何理解这个“保护”，以及“保护”的是什么东西？知乎上已经有相关的问题和诸多优秀的答案：

相较于已有的回答，本文可能没有什么太新的东西，唯一的优点是比较详（luo）细(suo)吧（手动狗头）。

”破坏“的描述

谈到保护，那么必然对应着破坏，对系统的“破坏”最常见的来源就是杂质。当系统的杂质尚不足于改变整个体带的时候，杂质的作用可以理解为对干净体现本证态的散射，可以通过一个散射矩阵来描述。这个过程如图示：

我们可以先将讨论放在前文画出BHZ模型能带时候的情况下：一个方向具有周期性（/无穷大）边界条件、，一个方向为有限（设为N个格点）,那么，这个系统的讨论可以视作一维的,那么态可以写作 | \psi \rangle = \sum_{l=1}^N a_l | l,\pm \rangle_c , \pm 标识内禀自由度，通常情况下即自旋自由度， c 意味着态是Current-normalized（ |l,\pm\rangle_c=\frac{1}{\sqrt{|v_{l,\pm}|}}|l,\pm\rangle; v_{l,\pm}=\frac{dE(k)}{dk}| _{k=k_{l,\pm}} ）的,可看作整个散射过程只散射一个电子。由于我们要考虑杂质的散射过程，我们需要通过L,R来标识杂质两边的态，in/out标识入射和出射态。以N个 |l,\pm\rangle_c 态为基，我们有：

a^{(in)}=\left( a_{L,1}^{in},a_{L,2}^{in},...,a_{L,N}^{in};a_{R,1}^{in},a_{R,2}^{in},...,a_{R,N}^{in}\right)\\ a^{(out)}=\left( a_{L,1}^{out},a_{L,2}^{out},...,a_{L,N}^{out};a_{R,1}^{out},a_{R,2}^{out},...,a_{R,N}^{out}\right)

两个矢量的长度加起来等于2*2*N，两个2一个来自内禀自由度，一个来自我们对L,R的区分。散射矩阵自然可以写作： S = \left( \begin{array} { l } { r}&{ t ^ { \prime } } \\ { t}& {r ^ { \prime } } \end{array} \right) 具有关系 a^{(out)}=Sa^{(in)} ,r,r'为 N\times N 的 反射矩阵 ，t,t'为 N\times N 的 透射矩阵 。本文剩下部分的内容主要是论证 当时间反演一直存在的时候，边缘态处这个散射是完全透射的 （ r=r'=0 ）。

边缘态附近的情况：一对Kramers边缘态

具有时间反演的体系，其边缘态总是分为可以 通过内禀自由度label 的两支，其速度 v_{l,\pm}=\frac{dE(k)}{dk}| _{k=k_{l,\pm}} 相等但反向，大致同下：

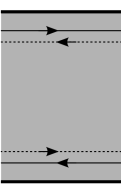
故边缘态的情况， \pm 既可以指代内禀自由度，也可以指代不同的传播方向。回到这个图：

对于边缘态处的一对Kramers简并态，一个态我们可以写作：

| \psi \rangle = \sum _ { l = 1 } ^ { N } \left[ a _ { L , l } ^ { ( \mathrm { in } ) } | l , + , L\rangle _ { c } + a _ { R , l } ^ { ( \mathrm { in } ) } | l , - , R \rangle _ { c }+ \left( S a ^ { ( \mathrm { in } ) } \right) _ { L , l } | l , - , L \rangle _ { c } + \left( S a ^ { ( \mathrm { in } ) } \right) _ { R , l } | l , + , R \rangle _ { c } \right]

由于边缘态的两个mode都具有相同的速度大小，同时前面我们采用的是current-normalized的基矢量，故这种情况下，S是酉矩阵。

接下来我们要讨论如果这个散射并不破坏时间反演对称意味着什么？

首先是内禀自由度为2的情况： | l , - , L \rangle _ { c } =\hat{\Theta} | l , + , L \rangle _ { c };| l , + , R \rangle _ { c } =-\hat{\Theta} | l , - , R \rangle _ { c }

然后对整个态做 \hat{\Theta} ，即取这个态的时间反演态:

\hat{\Theta}| \psi \rangle = \sum _ { l = 1 } ^ { N } \left[ a _ { L , l } ^ { ( \mathrm { in } )* } | l , - , L\rangle _ { c } + a _ { R , l } ^ { ( \mathrm { in } )* } | l , + , R \rangle _ { c }+ \left( -S^* a ^ { ( \mathrm { in } ) *} \right) _ { L , l } | l , + , L \rangle _ { c } + \left(- S^* a ^ { ( \mathrm { in } ) *} \right) _ { R , l } | l , - , R \rangle _ { c } \right]\\ =\sum _ { l = 1 } ^ { N } \left[ S^{T}S^*a _ { L , l } ^ { ( \mathrm { in } )* } | l , - , L\rangle _ { c } + S^{T}S^*a _ { R , l } ^ { ( \mathrm { in } )* } | l , + , R \rangle _ { c }+ \left( -S^* a ^ { ( \mathrm { in } ) *} \right) _ { L , l } | l , + , L \rangle _ { c } + \left(- S^* a ^ { ( \mathrm { in } ) *} \right) _ { R , l } | l , - , R \rangle _ { c } \right]

由于时间反演态具有相同的能量，其各个基态前面的系数应该具有 和该态相同的形式：

\hat{\Theta}|\psi\rangle=| \psi \rangle_{TR} \\| \psi \rangle_{TR} = \sum _ { l = 1 } ^ { N } \left[ a _ { L , l ;{TR} } ^ { ( \mathrm { in } ) } | l , + , L\rangle _ { c } + a _ { R , l;{TR} } ^ { ( \mathrm { in } ) } | l , - , R \rangle _ { c }+ \left( S a ^ { ( \mathrm { in } ) }_{TR} \right) _ { L , l } | l , - , L \rangle _ { c } + \left( S a ^ { ( \mathrm { in } ) }_{TR} \right) _ { R , l } | l , + , R \rangle _ { c } \right]

对比，即 \left(- S^* a ^ { ( \mathrm { in } ) *} \right)=a^{(in)}_{TR} ，从而给出 S^T=-S （由于我们内禀自由度为2，故自然是在 \hat{\Theta}^2=-1 的情况），对于 \hat{\Theta}^2=1 的情况，我们会发现 S=S^T 。由 S^T=-S\Rightarrow \left( \begin{array} { l } { r}&{ t ^ { \prime } } \\ { t }&{r ^ { \prime } } \end{array} \right) = \left( \begin{array} { c c } { - r^T } & { - t ^T} \\ { - t ^ { \prime T} } & { - r ^ { \prime T} } \end{array} \right) ，即 t=-t'^{T} , r=-r^{T},r'=-r'^{T}

"保护"

t=-t'^{T} , r=-r^{T},r'=-r'^{T} 这三个关系便能够讨论处很多的物理结论，无论 t 的情况如何， r=-r^T\Rightarrow det|r|=det|-r^T|=(-1)^N det|r^T|=(-1)^N det|r| 。当N为奇数的情况， det|r|=-det|r|\Rightarrow det|r|=0 ，(r'同样)， 意味着r必然含有一个0的本征值，即存在一个（散射矩阵的）本征态为完全透射 。用凝聚态的语言来说，这个本征值为0时候的本征态无法被gap掉。 回顾整个过程，散射理论是普适的，边缘态的出现来自于原来哈密顿的本身，我们能说明一件事，当N为奇数，如这个散射是不破坏时间反演对称的话，那么就会出现完全透射的态 。

End

基于完整性，还是把这篇文章更了，本文主要给出了一个角度&方法去思考和证明“ 对称保护 ”这一概念，虽然其实大体内容列出前面的知乎问题下的回答都涵盖了，对读者的贡献可能在于用于在于初学者可以简单看一看一个证明过程，直接阅读英文资料的时候，如果存在理解上的困惑能够参考下。PS：如有补充和不对的地方，欢迎评论区指出。

参[ban]考[yun]文[lai]献[yuan]

1. 《A Short Course on Topological Insulators: Band-structure topology and edge

states in one and two dimensions》

2.《 Topology in Condensed Matter 》Delft理工的拓扑课