float3x3 modelMatrixInv = unity_WorldToObject;
float3 normalDirection = normalize(mul(v.normal, modelMatrixInv));
That’s is very strange because the first one works perfectly when calculating specular on the fragment shader.
Thanks a lot.
I actually usually use a 3x3 version of UNITY_MATRIX_MVP. Side note is that this only works if the object has an uniform scale. As far as I can see, that also goes for using unity_WorldToObject.
You always want to use the 3x3 version if you are transforming a direction. Else the translation gets added and that’s not what you want for a direction vector. That’s not very strange and doesn’t depend on the vertex or fragment shader. Things probably got batched or were at the origin to begin with during your fragment shader test. Then it accidentally works correctly.
Generally the correct order for transforming vectors is what you see when transforming the vertex to world space or clip space, i.e.:
result = mul(matrix, vector)
However doing a mul in the opposite order does the multiplication of the matrix and the vector in a different order; the matrix is transposed.
mul(matrix, vector) == mul(vector, transpose(matrix))
mul(transpose(matrix), vector) == mul(vector, matrix)
So what’s happening with normals is the matrix mul is the inverse transform of the object to world matrix. For reasons which I won’t go into here the correct way to calculate a normal is by using the inverse transform of the model matrix (aka the unity_ObjectToWorld). Inverse matrices are expensive to calculate, but luckily the inverse of the object to world, or unity_ObjectToWorld, is already given to the shader as unity_WorldToObject. So why not just do mul(transpose(unity_WorldToObject), float4(normal.xyz, 0))? Because the transpose() function isn’t that fast either. It’s not really expensive as much as it creates less optimal shaders, and thus slower shaders, than just reversing the order in the mul().
@jvo3dc 's explanation for why the two versions of your normal matrix multiplication is also accurate. If you do a mul using a float4x4 matrix and a float4 vector with the w component with a value of 1 the matrix’s positional transform will be applied, where as if the w component is 0 it is not. In short float4(normal.xyz, 1) means the normal is rotated and moved, float4(normal.xyz, 0) is just rotated. Using a mul with a float4x4 matrix and a float3 vector is ambiguous though, and some shader compilers will understand that as you wanting to do a mul of a float3x3 matrix and a float3 vector, but some will expand out the float3 to a float4 with a w of 1, and others will just tell you it’s broken (sometimes with entirely unhelpful errors like “cannot create non square matrix”. You can also convert the float4x4 matrix to a float3x3 with no performance penalty.
mul(matrix, float4(vector.xyz, 0)) == mul((float3x3)matrix, vector.xyz)
Also, @jvo3dc 's comment about it “only works if the object has an uniform scale” is the exact reason why normals use an inverse transpose mul rather than the the same matrix as the vertices (and tangents!) use.
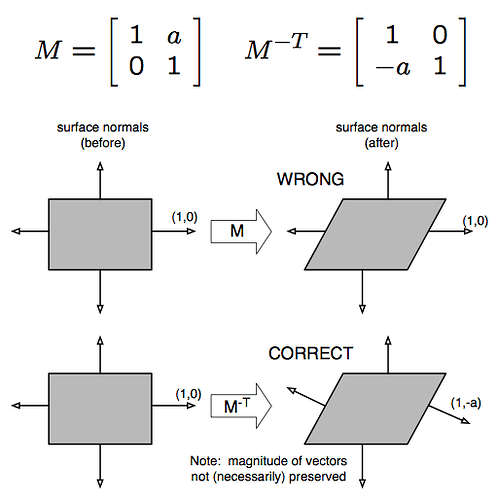
This image stolen from stackoverflow on the topic (the first link when googling “inverse transpose normal”) is a good visualization of what happens when using the model transform directly vs the inverse transpose on normals (though this example is actually showing a skew and not a non-uniform scale).
 bgolus:
bgolus:
Generally the correct order for transforming vectors is what you see when transforming the vertex to world space or clip space, i.e.:
I’m stuck on some piece of code that transforms a vector in world space to an object space by doing mul(vector, unity_ObjectToWorld). Finally understood why! Thank you so much!