论文题目:Vehicle Re-Identification by Deep Feature Fusion Based on Joint Bayesian Criterion(ICPR)
Abstract:
车辆重识别不同于行人重识别,其挑战性在于同种款式的不同车辆之间差异十分细小。本篇论文提出了双网络深度融合特征,两个网络可以提取输入图像的不同层面的特征并可以互相补充。通过提出的联合贝叶斯损失可以优化不同层面深度特征的融合,进而最小化类内间距,最大化类间间距,比较适合于车辆重识别任务。
Framework:
本文使用两个CNN网络来提取不同层面的特征,CNN1为CaffeNet,CNN2类似于NIN,其MLP卷积层具有很好的局部抽象能力。在得到两个网络的特征后,使用三层全连接网络进行特征融合,最后使用Softmax损失与联合贝叶斯判别损失进行了联合优化,获取强大的判别能力。
CaffeNet是一个小型网络,主要由5个卷积层、3个池化层、2个norm层与3个全连接层。结构如下:
NiN网络中的mlpconv卷积结构可以增强模型在
感受野(receptive field)
内对局部区域(local patches)的辨别能力。
类似的CNN2具体组成如下表:
普通卷积与mlp卷积的比较:
中间使用了两个1x1卷积与非线性操作,进行了所有通道间特征块的一个感知融合,具有更好的局部特征感知提取能力。
贝叶斯判别损失:
贝叶斯方法在人脸验证应用中具有很好的效果。
车辆特征可以由两部分组成,一部分是正确的身份信息,一部分是身份偏差,两者都服从高斯分布。
其中
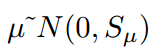 ,
,
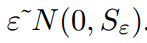 ,假设有两辆车的特征x1,x2,Hi表示同一车辆假设,He表示不同车辆假设。
,假设有两辆车的特征x1,x2,Hi表示同一车辆假设,He表示不同车辆假设。
两者的分布分别为
 ,它们各自的协方差如下:
,它们各自的协方差如下:
联合贝叶斯概率比:
贝叶斯损失如下定义:
softmax损失:
网络的整体损失:
实验结果:
试验在VehiclleID数据集上取得了很不错的效果,而且数据量越大,优势越明显。
多种层面特征融合是比较很好的应用技巧,而使用的贝叶斯损失很好地引导这个特征的融合。
论文题目:Vehicle Re-Identification by Deep Feature Fusion Based on Joint Bayesian Criterion(ICPR)Abstract:车辆重识别不同于行人重识别,其挑战性在于同种款式的不同车辆之间差异十分细小。本篇论文提出了双网络深度融合特征,两个网络可以提取输入图像的不同层面的特征并可以互相补充。通过提出的联合贝叶斯损...
概念、基本术语
信息
融合
:将来源不同的信息整合到一起,去冗余;得到的
融合
信息将利于我们之后的分析处理。
信息
融合
分为三个层次:数据
融合
,
特征
融合
,决策
融合
。如下图所示:
特征
融合
的分类
特征
融合
算法主要可以分为三类:
1.基于
贝叶斯
决策理论的算法
2.基于稀疏表示理论的算法
3.基于
深度
学习理论算法
基于
贝叶斯
理论的
特征
融合
算法
已知模式空间包含种模式,记为:,未知样本由维实值
特征
组成,记为.根...
后端
融合
常见的后端
融合
方式包括最大值
融合
(max-fusion)、平均值
融合
(averaged-fusion)、
贝叶斯
规则
融合
(Bayes’rule based)以及集成学习(ensemble learning)等
中间
融合
以神经网络为例,中间
融合
首先利用神经网络将原始数据转化成高维
特征
表达,然后获取不同模态数据在高维空间上的共性。
之前说过根据
融合
算法,可以概括为随机类方法和人工智能两大类。随机类方法目前常见的有加权平均法、多
贝叶斯
估计法、卡尔曼滤波法、Dempster-Shafer(D-S)证据推理、产生式规则等。人工智能类则主要包括模糊逻辑理论、神经网络、粗集理论、专家系统等。这边文章主要按照
融合
算法进行简单总结。
1.加权平均方法
优点:信息丢失量较小,可以方便的对初始数据进行
融合
。
缺点: 必须找到恰当的数学模型,适用范围较为有限。
2.卡尔曼滤波的方法
优点:数据所要传达的信...
举个例子:生病的几率
一种癌症,得了这个癌症的人被检测出为阳性的几率为90%,未得这种癌症的人被检测出阴性的几率为90%,而人群中得这种癌症的几率为1%,一个人被检测出阳性,问这个人得癌症的几率为多少?
https://www.zhihu...
1.
特征
表示
人脸由两个高斯变量的和表征:x=μ+εx=\mu+\varepsilonx=μ+ε
这里xxx代表人脸,μ\muμ代表固有身份,ε\varepsilonε代表脸部变化(光照,姿态,表情等)。隐变量μ\muμ代表固有身份,ε\varepsilonε服从高斯分布 N(0,Σε)\ N(0, \Sigma \varepsilon) N(0,Σε),N(0,Sε)N\left(0, S_{\varepsilon}\right)N(0,Sε)
以照片xix_{i}xi和xjx_{
基于
贝叶斯
决策理论的
特征
融合
是一种将不同
特征
信息进行
融合
的方法,其中利用了
贝叶斯
决策理论来进行决策。
贝叶斯
决策理论是一种基于概率的决策方法,它利用先验概率和条件概率来进行决策。在
特征
融合
中,可以利用
贝叶斯
决策理论来计算不同
特征
的后验概率,并基于这些后验概率进行最终的决策。
以下是一种基于
贝叶斯
决策理论的
特征
融合
的步骤:
1. 收集不同类型的
特征
数据,例如时域
特征
、频域
特征
、小波
特征
等。
2. 根据样本数据计算每种
特征
的先验概率。
3. 计算每种
特征
在不同类别下的条件概率。
4. 对于一个新的样本,计算其在每个类别下的后验概率。
5. 根据后验概率进行最终的决策,选择具有最高后验概率的类别作为最终决策结果。
在MATLAB中,可以使用统计工具箱中的函数来实现基于
贝叶斯
决策理论的
特征
融合
。例如,可以使用`fitcnb`函数来训练一个朴素
贝叶斯
分类器,并使用`predict`函数来进行分类预测。
通过基于
贝叶斯
决策理论的
特征
融合
方法,可以充分利用不同
特征
的概率信息,提高分类的准确性和鲁棒性,在模式
识别
、图像处理等领域中具有广泛的应用。
RuntimeError: The Session graph is empty. Add operations to the graph before calling run()
25024
视觉弘毅: