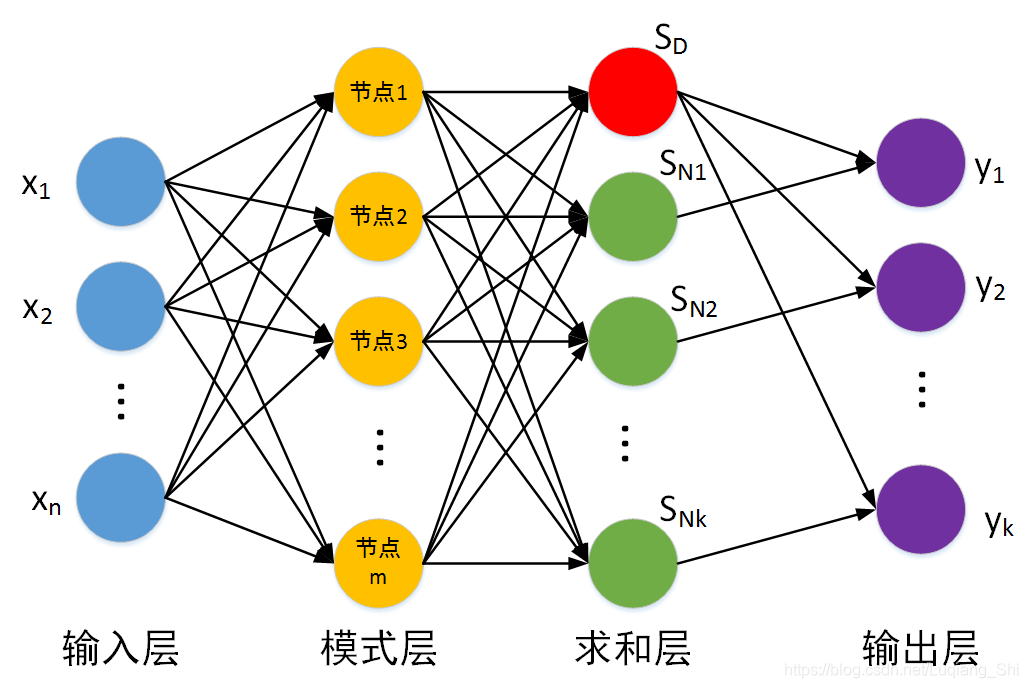
如下图所示,GRNN与PNN一样也是一个四层的网络结构。
对于回归问题训练数据集包括样本特征集与标签集,假设样本特征集为:
{ t r x 1 , t r x 2 , ⋯   , t r x m } \left\{ {tr{x_1},tr{x_2}, \cdots ,tr{x_m}} \right\}
{
t
r
x
1
,
t
r
x
2
,
⋯
,
t
r
x
m
}
,每一个样本的维度为
n n
n
,即
t r x i = [ x 1 , x 2 , ⋯   , x n ] tr{x_i} = [{x_1},{x_2}, \cdots ,{x_n}]
t
r
x
i
=
[
x
1
,
x
2
,
⋯
,
x
n
]
。标签集为:
{ t r y 1 , t r y 2 , ⋯   , t r y m } \left\{ {tr{y_1},tr{y_2}, \cdots ,tr{y_m}} \right\}
{
t
r
y
1
,
t
r
y
2
,
⋯
,
t
r
【机器学习】广义回归神经网络(GRNN)的python实现一、广义回归神经网络原理1.1、GRNN与PNN的关系2.2、GRNN的网络结构二、广义回归神经网络的优点与不足2.1、优点2.2、不足三、GRNN的python实现参考资料一、广义回归神经网络原理1.1、GRNN与PNN的关系广义回归神经网络(Generalized Regression Neural Network)的网络结构类似...
广义
回归
神经网络
(G
RNN
)
广义
回归
神经网络
是径向基
神经网络
的一种,G
RNN
具有很强的非线性映射能力和学习速度,比
RBF
具有更强的优势,网络最后普收敛于样本量集聚较多的优化
回归
,样本数据少时,预测效果很好,还可以处理不稳定数据。虽然G
RNN
看起来没有径向基精准,但实际在分类和拟合上,特别是数据精准度比较差的时候有着很大的优势。
关于
RBF
,G
RNN
与PNN
RBF
网络是一个两层的网络,...
G
RNN
广义
回归
神经网络
以非参数核
回归
为基础,以样本数据作为后验概率验证条件并进行非参数估计,最后从训练样本中计算G
RNN
网络中因变量和自变量之间的关联密度函数,从而计算得到因变量相对自变量的
回归
值。G
RNN
广义
回归
神经网络
最大的优势在于其方便的网络参数设置功能,整个
神经网络
只需要通过设置G
RNN
核函数中的光滑因子就可以调整G
RNN
网络的性能。
假设G
RNN
神经网络
中的两个随机变量x和y,其联合概率密度函数为f (x ,y),且x的观测样本为X,即条件均值为:
公式4即为人...
1.版本:matlab2021a,我录制了仿真操作录像,可以跟着操作出仿真结果
2.领域:时间序列预测
3.内容:基于G
RNN
广义
回归
神经网络
的时间序列预测matlab仿真
4.适合人群:本,硕等教研学习使用
【
机器学习
】最小二乘法支持向量机LSSVM的数学原理与
Python
实现
一、LSSVM数学原理1. 感知机2. SVM3. LSSVM4. LSSVM与SVM的区别二、LSSVM的
python
实现
参考资料
一、LSSVM数学原理
1. 感知机
SVM是从感知机发展而来。假设有m个训练样本{(xi,yi)}i=1m\left\{ {\left. {\left( {{x_i},{y_i}} \right...
【
机器学习
】
RBF
神经网络
原理与
Python
实现
一、LSSVM数学原理1. 感知机2. SVM3. LSSVM4. LSSVM与SVM的区别二、LSSVM的
python
实现
参考资料
一、LSSVM数学原理
1. 感知机
SVM是从感知机发展而来。假设有m个训练样本{(xi,yi)}i=1m\left\{ {\left. {\left( {{x_i},{y_i}} \right)} \right\}...
【寻优算法】遗传算法(Genetic Algorithm) 参数寻优的
python
实现
:多参数寻优一、遗传算法简介1、遗传算法由来2、遗传算法名词概念3、遗传算法中对染色体的操作3.1、选择3.2、交叉3.3、变异二、遗传算法多参数寻优思路三、遗传算法多参数寻优的
python
实现
参考资料
本博文首先简单介绍遗传算法(GA)的基础知识,然后以为例给出遗传算法多参数寻优的
python
实现
。
一、遗传算...
def predict(self, X_test):
n_samples = self.X.shape[0]
G = np.exp(-np.sum((np.tile(X_test, (n_samples, 1)) - self.X)**2, axis=1) / (2*self.sigma**2))
y_pred = np.sum(G*self.y) / np.sum(G)
return y_pred
这个
实现
代码中使用了numpy库来处理矩阵运算,G
RNN
的核心公式为:
$$G_i = e^{-\frac{\sum_{j=1}^{n}(x_{test,j}-x_{i,j})^2}{2\sigma^2}}$$
$$y_{pred} = \frac{\sum_{i=1}^{n}G_i y_i}{\sum_{i=1}^{n}G_i}$$
其中,$G_i$是第$i$个样本点到测试点的高斯核值,$y_i$是第$i$个样本点的标签值,$y_{pred}$是预测值,$\sigma$是超参数,用于控制高斯核的宽度。
