从类型兼容开始,认识 TypeScript
类型兼容
在 TypeScript 编程中,类型兼容是最基础的一道检查机制,一旦代码中出现类型不兼容的表达式,编译就会失败。
- 赋值表达式中,右值输出到左值需要类型兼容。如下:
const foo: 233 = 233;
const bar: number = foo;
- 函数调用表达式中,实参输出到形参需要类型兼容。如下:
declare function log(x: number /*形参*/): unknown;
const foo: 233 = 233;
log(foo /*实参*/);- 函数表达式中,函数体输出的类型需要兼容返回值类型。如下:
function mysteryBox(): number {
const foo: 233 = 233;
return foo;
}向下兼容
TypeScript 的类型兼容总是向下兼容的。
得到输入的 A 总是要求输出的 B 拥有 A 类型的一切特性,以致于 A 能表现出的特性在实际使用中不会缺失,从而保证程序正确。
集合的角度
从集合的角度出发能让我们更好地理解向下兼容。
当我们把类型 T 视为集合 S 时,S 由全部的满足 T 一切特性的元素组成,S 的每一个元素都满足 T ,S 的每一个子集都满足 T 。 - 此时,将 S 的任一子集视为新的类型 T1 。T1 拥有 T 的一切特性,T1 向下兼容 T 。 - 同样的,将能够向下兼容 T 的任一类型视为新的集合 S1 。S1 满足 T ,S1 包含于 S ,S1 是 S 的子集。
由此可得, 子类型向下兼容超类型如同子集包含于超集 。
维恩图
我们可以用表示集合关系的维恩图,表达类型间的兼容关系。如前文出现的类型
233
和类型
number
:

-
233向下兼容number。 -
233是number的子类型,233是number的子集。 -
number是233的超类型,number是233的超集。
认识
as
、
extends
、
infer
本文将从类型兼容的角度,辅以集合的概念,重新认识
as
、
extends
、
infer
等 TypeScript 符号。
类型断言
as
不知道在阅读的你是否有留意过
as
的报错,里面提到过“两种类型不能充分重叠……”如下:
// Conversion of type 'number' to type 'string' may be a mistake because neither type sufficiently overlaps with the other. If this was intentional, convert the expression to 'unknown' first.(2352)
// 类型 "number" 到类型 "string" 的转换可能是错误的,因为两种类型不能充分重叠。如果这是有意的,请先将表达式转换为 "unknown"。ts(2352)
233 as string;充分重叠
如果把“充分重叠”这个词放在类型是集合的上下文中,那么就能更容易理解这些报错的含义了。
我们不妨这么认为,当集合 B 是集合 A 的子集时,集合 B 的元素选取范围就与集合 A 的元素选取范围“充分重叠”。 (如同上文维恩图所示。)
不充分重叠的时候,意味着 A 包含有不属于 B 的元素,B 也包含有不属于 A 的元素。
显然,在我们的编程经验中,
number
和
string
不是充分重叠的。这是导致
233 as string
报错的直接原因。
unknown
同时,上文的报错提示我们,“如果这是有意的,请先将表达式转换为 "unknown"。”
233 as unknown as string; // 编译通过
为什么
as unknown as
可以发挥作用?我们可以先分析一下
unknown
类型。
从
文档
可知,任何类型都能分配给
unknown
。这等同于任何类型都能向下兼容
unknown
。
因为任何类型都向下兼容
unknown
,所以
unknown
是任何类型的超类型!
(也是超集。)
已知,
number
是
unknown
的子集,与
unknown
充分重叠;
string
是
unknown
的子集,与
unknown
充分重叠。
上文的报错侧面告诉我们,
只要是充分重叠的两个类型,就能使用
as
完成转换。
因此,将
233 as unknown as string
分成两步判断,
233 as unknown
和
unknown as string
都是合法的,可以通过编译的。
如果用维恩图表示
number
,
string
和
unknown
之间的关系,则是这样的:
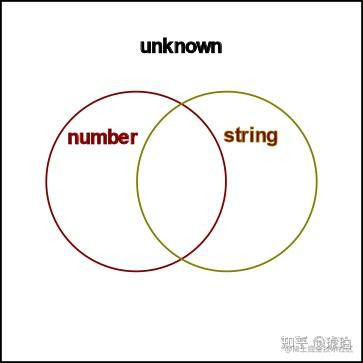
-
number和string没有包含关系,不能充分重叠。 -
number是unknown的子集,与unknown充分重叠。 -
string是unknown的子集,与unknown充分重叠。
number | string
如果将
number
和
string
的合集视为一个类型,该类型也能与
number
或
string
充分重叠。那么,该类型能否代替
233 as unknown as string
中的
unknown
发挥作用?在此之前,如何构造出这个类型呢?
TypeScript 提供了
联合类型
的运算符
|
。从语义上看,这个运算符似乎可以联合两个类型,得到他们的合集。
我们不妨用
|
做一次实验:
type Chimera = number | string;
233 as Chimera as string;
const foo: Chimera = 233;
const bar: Chimera = "hello";
declare const baz: Chimera;
const qux: number = baz; // 不能向下兼容,报错了
const zoo: string = baz; // 不能向下兼容,报错了-
Chimera代替233 as unknown as string中的unknown发挥作用了。 -
Chimera如同number和string共同的超类型,被number或string向下兼容,发挥着超类型的作用。 -
而
Chimera不能向下兼容number或string。number和string都是Chimera的真子集,number或string与Chimera不相等。
由此可得,
|
运算符可以联合两个类型,得到他们的合集。
同时也是他们的共同超类型。而且,在
as
表达式中,只要一边是超类型就能使其合法。
number & string
同样的,如果将
number
和
string
的交集视为一个类型,该类型也能与
number
或
string
充分重叠。那么,该类型能否代替
233 as unknown as string
中的
unknown
发挥作用?在此之前,如何构造出这个类型呢?
TypeScript 提供了
交叉类型
的运算符
&
。从语义上看,这个运算符似乎可以交叉两个类型,得到他们的交集。
我们不妨用
&
做一次实验:
type Chimera = number & string;
233 as Chimera as string;
const foo: Chimera = 233; // 不能向下兼容,报错了
const bar: Chimera = "hello"; // 不能向下兼容,报错了
declare const baz: Chimera;
const qux: number = baz;
const zoo: string = baz;-
Chimera代替233 as unknown as string中的unknown发挥作用了。 -
number和string都不能向下兼容Chimera。 -
而
Chimera如同number和string共同的子类型,可以向下兼容number或string,发挥着子类型的作用。
由此可得,
&
运算符可以交叉两个类型,得到他们的交集。
同时也是他们的共同子类型。而且,在
as
表达式中,只要一边是子类型就能使其合法。
as
的成立条件
类型断言(
as
)的
文档
有那么一句话:
TypeScript only allows type assertions which convert to a more specific or less specific version of a type.
其中, more specific 和 less specific ,字面意思是更具体和更不具体,也许可以用大家更熟悉的词汇代替, 更具体 和 更抽象 。
如此之后,引用的句子可以翻译为:
类型断言只能把类型转换成更具体或更抽象的版本。
结合前文,我们不妨认为, 类型更具体的版本 和他的子类型是等价的, 类型更抽象的版本 和他的超类型是等价的。
由此可得,
as
运算符两边的类型,只有在它们存在集合间的包含关系才能够成立。
never
在
type Chimera = number & string
的举例中,TypeScript 会将其推导成
type Chimera = never
: -
number
和
string
的交集是
never
!? -
as never as
难道和
as unknown as
一样,能用于通用的类型转换?
从
文档
可知,
never
可以分配给任何类型。这等同于
never
能向下兼容任何类型。
因为
never
能向下兼容任何类型,所以
never
是任何类型的子类型!
在集合论中,空集是任何集合的子集。我们不妨认为
never
和空集是等价的。
因此,
number
和
string
的交集是
never
时,意味着
number
和
string
没有任何相同的元素。或者说不存在一个元素能同时具备
number
和
string
的特性。这很符合我们的编程经验。
因为
unknown
与任何类型“充分重叠”,所以
as unknown as
能用于通用的类型转换。而作为任何类型的子类型的
never
,无疑与任何类型“充分重叠”,所以
as never as
能用于通用的类型转换。
如果用维恩图表示
number
,
string
,
unknown
,
never
之间的关系,则是这样的:
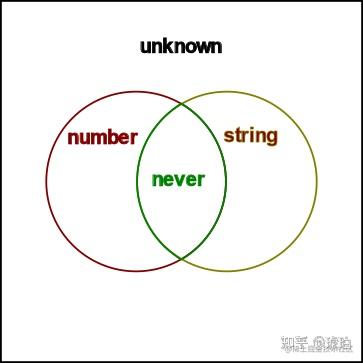
-
number
&
string
为
never
。 -
number
和
string
都是
unknown
的子集。
&
和
|
以及超集和子集
如果我们让
never
和
number
再次相交,如同一个集合和它的超集相交。根据集合的性质,得到的交集就会是该集合本身。如下:
type foo = never & number; // type foo = never
type bar = never & string; // type bar = never-
&表现出求交集的运算。 -
never与任何类型相交都会得到never。
而一个集合和它的子集合并,得到的并集就是该集合本身。如下:
type foo = unknown | number; // type foo = unknown
type bar = unknown | string; // type bar = unknown-
|表现出求交集的运算。 -
unknown与任何类型合并都会得到unknown。
同样的:
type foo = never | number; // type foo = number
type bar = unknown & string; // type bar = string
如果结合了上文维恩图的包含关系,那么就能更容易理解
&
和
|
在类型上的运算。
any
前面提及过任何类型的超集
unknown
和任何类型的子集
never
,那另一个跟任何类型密切相关的
any
呢?如何从集合的角度去看待他与其他类型的包含关系。
any
太特殊了,我无法用集合的语言表达。~~维恩图不会画了。~~
但我可以从包含途径出发,画出以下图表:
flowchart RL
any --> never
number --> any
string --> any
rest1[...] --> any
rest2[...] --> number
rest3[...] --> string
unknown[unknown / any] --> rest1
unknown --> rest2
unknown --> rest3- 箭头左边的项包含于右边的项。
-
any在 TypeScript 中可以兼容never以外任何的类型,我们不妨认为他是never以外任何类型的子类型,同时也是任何类型的超类型。因此上图有两个any。
结构化类型
重新认识 extends 之前,我们有必要了解 结构化类型 。
TypeScript 的结构化类型系统是根据 JavaScript 代码的典型写法设计的。
JavaScript 广泛使用了函数表达式和对象字面量,结构化类型就是针对这点设计的,他们在字面表达上有非常相似的地方。
而结构化类型的字面表达,与泛型类型、条件类型,类型推导等类型操作关系密切。
常见的结构化类型有以下几种。
基元类型 ( Primitives )
基元类型就是那些平坦的字面值类型,
string
,
number
,
boolean
等等。
记录类型( Record / Object Types )
记录是一系列属性的组合。如下:
let foo: { name: string; age: number }; // 属性表达式
let bar: { [index in string]: number }; // 索引签名表达式
foo = { name: "foo", age: 23 };
bar = { x: 233 };也有人称之为对象类型,但是我为了消除歧义,更愿意称之为记录类型。
数组类型( Array )
数组类型就是数组的类型。如下:
let foo: number[];
foo = [1, 2, 3];元组类型( Tuple )
元组是一系列属性的排列,在 TypeScript 中元组也属于数组的一种。如下:
let foo: [name: string, age: number];
let bar: [string, number]; // 省略属性名的形式。
foo = ["foo", 23]; // 元组类型特性在于属性的排列分布,属性名只是记号,不存在于元组值中。
bar = ["bar", 33];函数类型( Function )
函数类型就是函数的类型。如下:
let foo: (x: string) => unknown;
foo = (x) => console.log(x);结构化类型在分配时,也是需要向下兼容的。我们接下来谈谈其中几个在类型兼容方面的表现。
(谈论之前或许还需要一个前提,结构化类型所表达的值是不可变的、无状态的。这样可以避免过早考虑逆变的问题。)
记录类型
记录通过属性名对外输出属性。直观上,两个记录类型若要存在兼容关系:
- 子类型拥有超类型的一切同名属性。
- 子类型的同名属性一一向下兼容超类型的同名属性。
如下:
declare let foo: { a: number; b: string };
declare let bar: { a: number };
declare let baz: { a: unknown };
baz = bar = foo;
foo = bar = baz; // 不能向下兼容,报错了-
{ a: number }拥有{ a: unknown }同名属性a,同名属性类型number向下兼容unknown,因此{ a: number }向下兼容{ a: unknown }。 -
{ a: number; b: string }拥有{ a: number }的同名属性a,同名属性类型相同,类型相同即相互向下兼容。因此{ a: number; b: string }向下兼容{ a: number }。 - 反之则不能向下兼容。
记录类型的交集
两个集合的交集是它们的共同子集。当这些集合代表记录类型时,意味着两个记录类型相交得到的共同子类型,拥有它们的一切属性。而子类型中名字重复的属性,它们的类型将两两相交,以致于能同时向下兼容两个超类型的对应属性。
在文档对交叉类型的
介绍
中,运算符
&
本来就是用于组合多个记录类型。
如下:
type Chimera = { a: unknown; b: string } & { a: number };
declare let foo: { a: number; b: string };
declare let bar: Chimera;
bar = foo;
foo = bar;-
Chimera拥有{ a: unknown; b: string }和{ a: number }的一切属性a和b。 -
同名属性
a的类型由unknown和number两两相交而得。 -
综上,
Chimera至少拥有a: number和b: string两个属性,将向下兼容{ a: number; b: string }。
当两个集合互为子集时,两个集合相等。同样的, 当两个类型互为子类型时,也就是相互向下兼容时,两个类型相等 。
因此
{ a: unknown; b: string } & { a: number }
等同于
{ a: number; b: string }
。
相关维恩图:

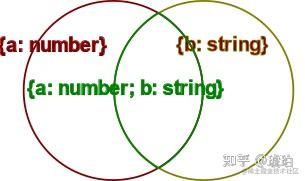
{}
{}
是一个没有任何属性的组合,显然他的类型会被任何记录类型向下兼容,是任何记录类型的超类型。
如下:
declare let foo: { a: number };
declare let bar: { b: string };
declare let baz: {};
baz = foo;
baz = bar;
特别的,JavaScript 里非
null
/
undefined
的值,都能像 JavaScript 对象那样访问属性。反映在 TypeScript 中,类型
{}
是非
null
/
undefined
值类型的超类型。
如下:
type foo = {} & null; // type foo = never
type bar = {} & undefined; // type bar = never
type baz = {} & number; // type baz = number
type qux = {} & string; // type qux = string-
通过求交集的方式,得出
{}与null/undefined没有包含关系。 -
通过求交集的方式,得出
{}是number/string的超集、超类型。
( typescript-eslint 认为
{}
代表着非空的值,不是大众预期的“空对象”,从而
不推荐使用
。)
有两个问题留给大家思考: 1. JavaScript 的
number
经过装箱成为
Number
对象后,能表现出 JavaScript 对象的性质。请问,在 TypeScript 中
number
和
Number
的兼容关系是怎样的? 2. 如何定义出一个“空对象”类型,使得任何带有属性的记录类型不能向下兼容它。
数组类型
数组对外输出元素,数组类型的向下兼容体现在元素类型的向下兼容。如下:
declare let foo: number[];
declare let bar: unknown[];
bar = foo;
foo = bar; // 不能向下兼容,报错了-
number向下兼容unknown,number[]便向下兼容unknown[]。 - 反之则不能向下兼容。
特别的
unknown
是任何类型的超类型,
unknown[]
即是任何数组类型的超类型。

元组类型
元组通过排列顺序输出属性。直观上,两个元组类型若要存在兼容关系:
- 子类型的属性排列结构与超类型完全对应。
- 子类型与超类型排列对应的属性,其类型一一向下兼容。
如下:
declare let foo: [number, string];
declare let bar: [number];
declare let baz: [unknown];
bar = foo; // 不能向下兼容,报错了
baz = bar;
foo = bar; // 不能向下兼容,报错了
bar = baz; // 不能向下兼容,报错了-
[number, string]和[number]的属性排列结构不同,因此不能向下兼容。 -
[number]和[unknown]是相同的排列,number向下兼容排列对应的unknown,因此[number]向下兼容[unknown]。
相关维恩图:

rest
元组类型支持 rest 表达式,存在包含关系的两个元组类型,其属性数量不一定是相等的。
如下:
declare const foo: [number, boolean, string];
declare const bar: [number, string];
declare const baz: [string];
declare let qux: [...unknown[], string];
qux = foo;
qux = bar;
qux = baz;-
[number, boolean, string],[number, string]和[string]之间并不存在兼容关系。 -
但是他们都向下兼容
[...unknown[], string]。而[...unknown[], string]并没有固定的属性数量。
元组类型的交集
属性的排列结构显然是相斥的,而结构不同的两个元组类型的交集确实是
never
,是空集。如果结构相同的两个元组类型相交,每个对应的属性类型将两两相交,以致于能同时向下兼容两个超类型的对应属性。
如下:
type Chimera1 = [number, string] & [unknown]; // Chimera = never
type Chimera2 = [number] & [unknown];
declare let foo: Chimera2;
declare let bar: [number];
bar = foo;
foo = bar;-
[number, string]与[unknown]不相交,排列结构相斥。 -
[number] & [unknown]等同于[number]。
[]
[]
是一个没有任何属性的排列,与记录类型的共同超类型
{}
不同,元组类型的共同超类型不是
[]
。元组类型的共同超类型应该是
[...unknown[]]
,简化可得
unknown[]
。
如下:
declare let foo: [number, string];
declare let bar: [number];
declare let baz: unknown[];
baz = foo;
baz = bar;extends
在 TypeScript 中,有好几种表达式使用了
extends
这个关键字,而且具体作用各不相同。但他们都有相似的地方,如果
extends
左右两边都是类型,左边的类型将向下兼容右边的类型。
泛型约束
在泛型函数或泛型类型中,泛型参数列表中的
extends
可以约束泛型参数的类型,使得输出到泛型参数的类型必须向下兼容
extends
所约束的类型。这种约束被称为
泛型约束
。
如下:
declare const foo: { a: number; b: string };
function bar<T extends { a: number }>(x: T) {
const baz: number = x.a;
bar(foo);-
上文中的泛型约束是
T extends { a: number },输出到T的类型必须向下兼容{ a: number }。 -
{ a: number; b: string }向下兼容{ a: number },因此实参bar的类型向下兼容形参x的类型T,可以合法输入。 -
因为泛型约束,所以在函数定义的上下文中,
T确定向下兼容{ a: number },所以类型是T的参数x可以合法输出属性a。
泛型约束除了带来了泛型参数的类型限制,还为当前上下文带来了泛型参数的超类型信息。
条件类型
条件类型
一般出现在泛型函数或泛型类型中,是构造新类型的一种手段。他的表达式与
条件表达式
的形式很像,只是条件部分被固定为
extends
断言,当
extends
左右两边的向下兼容成立,就计算并返回第一条分支,反之则第二条分支。
如下:
type BelongToNumber<T> = T extends number ? true : false;
type Foo = BelongToNumber<1>; // type Foo = true
type Bar = BelongToNumber<string>; // type Bar = false-
BelongToNumber<T>就是条件类型,他需要输入具体的泛型参数才能具化成特定的结构化类型。 -
类型
1向下兼容number,因此BelongToNumber<1>得到第一条分支的结果true。 -
类型
string不向下兼容number,因此BelongToNumber<string>得到第二条分支的结果false。
(A extends B ? first : second)
如此形式的表达式,我为了方便讲述称之为
条件类型表达式
。并且称
A
为
条件类型表达式的子类型
,称
B
为
条件类型表达式的超类型
。
条件类型的分配律
当我们把联合类型作为泛型参数输入条件类型时,只要该泛型参数直接出现在 条件类型表达式的子类型 上,条件类型就会呈现出 分配律 。
分配律,简单地说就是,条件类型
T<A | B>
会按照
T<A> | T<B>
的方式进行解释。
如下:
type BelongToNumber<T> = T extends number ? true : false;
type Foo = BelongToNumber<1 | string>; // type Foo = boolean
type Bar = true | false; // type Bar = boolean-
泛型参数
T直接出现在条件类型表达式的子类型上。 -
BelongToNumber<1 | string>按照BelongToNumber<1> | BelongToNumber<string>的方式进行解释。 -
boolean只有两种取值可能true或false,将他们视为集合时,boolean是true和false的合集。因此true | false会得到boolean。
分配律就是你们想的那种分配律,如乘法分配律,
(A + B) × C = A × C + B × C
。乃至于,条件类型
T<A | B, C | D>
有可能得到
T<A, C> | T<A, D> | T<B, C> | T<B, D>
。
如下:
type Orthrus<A, B> = A extends unknown
? B extends unknown
? [A, B]
: never
: never;
type Foo = Orthrus<"A" | "B", "C" | "D">; // type Foo = ["A", "C"] | ["A", "D"] | ["B", "C"] | ["B", "D"]- 条件类型表达式允许嵌套表达。
-
泛型参数
A和B都直接出现在条件类型表达式的子类型上。 -
Orthrus<"A" | "B", "C" | "D">呈现了分配律。
如果只有泛型参数
A
直接出现在条件类型表达式的子类型上呢?如下:
type Orthrus<A, B> = A extends unknown ? [A, B] : never;
type Foo = Orthrus<"A" | "B", "C" | "D">; // type Foo = ["A", "C" | "D"] | ["B", "C" | "D"]- 同样呈现出了分配律。
抑制条件类型的分配律
有些时候我们并不希望条件类型呈现分配律。当泛型参数需要出现在条件类型表达式的子类型上时,可以将其类型参数在该位置上构造成其他类型,使其不再直接出现,从而导致分配律失效。
如下:
type BelongToNumber2<T> = T | number extends number ? true : false;
// type BelongToNumber2<T> = [T] extends [number] ? true : false;
// type BelongToNumber2<T> = T[] extends number[] ? true : false;
// type BelongToNumber2<T> = { x: T } extends { x: number } ? true : false;
type Foo = BelongToNumber2<1>; // type Foo = true
type Bar = BelongToNumber2<string>; // type Bar = false
type Baz = BelongToNumber2<1 | string>; // type Baz = false
type Qux = BelongToNumber2<1 | 2>; // type Qux = true-
泛型参数
T在条件类型表达式的子类型上被构造成其他类型,不再直接出现。 -
以上条件类型
BelongToNumber2<T>的几种构造方式,都能抑制条件类型的分配律,使其将泛型参数完整地输入。 - 而改造了子类型部分的类型后,需要对超类型部分进行对应的改造,使其表达出原来的类型兼容关系。
通过构造成元组类型来抑制条件类型的分配律是最简单直接的方式,也是官方文档所推崇的方式。
infer
条件类型最神奇的组件就是
infer
,他的语义是推断,能帮助我们推断出结构化类型的组成元素的类型。
infer
只能出现在
条件类型表达式的超类型
上,能作为超类型的字面表达式中的类型,并借此推断子类型的字面表达式中对应的类型。当条件类型表达式的兼容关系成立,就能在其第一条分支上使用推断得到的类型。
如下:
type Orthrus1<T> = T extends { a: infer X } ? X : never;
type Foo = Orthrus1<{ a: number; b: string }>; // type Foo = number
type Bar = Orthrus1<{ b: string }>; // type Bar = never
type Orthrus2<T> = T extends [infer X, string] ? X : never;
type Baz = Orthrus2<[number, string]>; // type Baz = number
type Qux = Orthrus2<[number]>; // type Qux = never
在条件类型
Orthrus1<T>
中: -
T extends { a: infer X }
表示,当
T
是
{ a: unknown}
的子类型时,
X
将被推断为类型
T
字面表达式中所对应的属性
a
的类型。 - 当输出到泛型参数
T
的类型是
{ a: number; b: string }
时,
X
被推断为
{ a: number; b: string }
所对应的属性
a
的类型
number
。同时也是满足了条件类型的断言,计算并返回第一条分支。 - 当输出到泛型参数
T
的类型是
{ b: string }
时,
{ b:string}
不能向下兼容
{ a: unknown}
。条件类型表达式的断言不成立,因此直接计算并返回第二条分支。
在条件类型
Orthrus2<T>
中: -
T extends [infer X, string]
表示,当
T
是
[unknown, string]
的子类型时,
X
将被推断为类型
T
字面表达式中所对应的位置的类型。 - 当输出到泛型参数
T
的类型是
[number, string]
时,
X
被推断为
[number, string]
所对应的位置的类型
number
。同时也是满足了条件类型的断言,计算并返回第一条分支。 - 当输出到泛型参数
T
的类型是
[number]
时,
[number]
不能向下兼容
[unknown, string]
。条件类型表达式的断言不成立,因此直接计算并返回第二条分支。
当你意识到结构化类型的字面表达是条件类型中的构成之一,意识到
infer
推断的是结构化类型的字面表达中被其取代的类型,就能迅速地掌握
infer
这个关键字。
infer ... extends ...
我们不难看出用
infer X
推断类型的时候,其实还隐含了一条泛型约束,那就是
X extends unknown
。只有
X
是
unknown
的子类型而不是别的具体类型的子类型,
X
才能替代条件类型表达式的超类型的字面表达式中的任意类型。
而
infer
也支持显式的泛型约束。不仅约束条件类型表达式的向下兼容断言,还为当前上下文提供被推断类型的超类型信息。
如下:
type Orthrus<T> = T extends { a: infer X extends number } ? X : never;
type Foo = Orthrus<{ a: number; b: string }>; // type Foo = number
type Bar = Orthrus<{ a: boolean; b: string }>; // type Bar = never-
条件类型表达式的超类型是
{ a: infer X extends number }。意味着,子类型部分需要向下兼容{ a: number },才能完成infer的推断,才能计算并返回第一条分支。 -
{ a: number; b: string }向下兼容{ a: number },因此X被推断为{ a: number; b: string }中属性a的类型number,然后在第一条分支返回X作为结果,最后Foo得到number。 -
{ a: boolean; b: string }不能向下兼容{ a: number },因此在第二条分支返回never作为结果,最后Bar得到never。
还为当前上下文提供被推断类型的超类型信息。
这属于技巧类的应用,此处不赘述。
泛型类型与类型兼容
泛型类型在输入所有具体的泛型参数后,可以实例化成具体的结构化类型。此时的结构化类型才能够进行分配,谈论类型兼容才有意义。
type MysteryBox<T> = T;
declare const foo: MysteryBox; // 未实例化的泛型类型无法作为变量的类型,报错了
declare let bar: MysteryBox<number>;
declare let baz: MysteryBox<unknown>;
baz = bar;
bar = baz; // 不能向下兼容,报错了-
MysteryBox不能直接作为变量的类型。 -
MysteryBox<number>向下兼容了MysteryBox<unknown>。
特别的,
MysteryBox<number>
向下兼容
MysteryBox<unknown>
,本质上是他们的计算结果
number
向下兼容了
unknown
。与泛型参数之间的兼容关系没有直接关系。
可以举一个反例,使得
T<number>
不能向下兼容
T<unknown>
。如下:
type MysteryBox<T> = { func: (x: T) => unknown };
declare let foo: MysteryBox<number>;
declare let bar: MysteryBox<unknown>;
bar = foo; // 不能向下兼容,报错了
foo = bar;-
MysteryBox<number>不能向下兼容MysteryBox<unknown>,是因为(x: number) => unknown不能向下兼容(x: unknown) => unknown。 -
MysteryBox<unknown>向下兼容MysteryBox<number>,是因为(x: unknown) => unknown向下兼容(x: number) => unknown。
可见泛型参数之间能够向下兼容,不代表泛型类型计算出来的类型能够向下兼容。
函数类型与类型兼容
函数类型的向下兼容似乎有些奇怪呢。仅从函数参数来看,上文参数
x
的类型
unknown
能兼容对应位置的
number
,不同于向下兼容。这是因为该类型参数是逆变的。
类型参数
类型参数是抽象的,当我们需要分析结构化类型中某个元素的类型,可以将该类型当作是一个参数,名曰类型参数。就像泛型参数做的那样。
函数类型的类型参数可以分为两种,一种位于函数参数列表作为参数类型,一种位于返回值签名作为返回值类型。
用泛型类型辅助说明会更清晰,如下:
type MysteryBox<In, Out> = (x: In) => Out;
type Foo = MysteryBox<number, unknown>; // type Foo = (x: number) => unknown-
MysteryBox<In, Out>的泛型参数In对应位于函数参数列表的类型参数;泛型参数Out对应位于返回值签名的类型参数。 -
与
MysteryBox<In, Out>对应的(x: number) => unknown,位于函数参数列表的类型参数的实际类型是number;位于返回值签名的类型参数的实际类型是unknown。
逆变
在函数类型中,位于函数参数列表的类型参数,他的类型分配方向,与函数类型本身的类型分配方向相反,这种表现被称为是逆变的。
如下:
declare let foo: (x: unknown) => unknown;
declare let bar: (x: number) => unknown;
declare let baz: 233;
bar = foo;
bar(baz);-
沿着参数输入的方向,参数类型
233分配给number分配给unknown。类型的合法分配依旧要满足向下兼容。 -
沿着函数赋值的方向,函数类型
(x: unknown) => unknown分配给(x: number) => unknown。合法的分配,表现出了向下兼容。
如此看来,类型依旧是向下兼容的。只不过,位于函数参数列表的类型参数是逆变的,随着函数类型本身向着超类型分配时,他允许向着自己的子类型进行分配。
协变
在函数类型中,位于返回值签名的类型参数,他的类型分配方向,与函数类型本身的类型分配方向一致,这种表现被称为是协变的。
如下:
declare let foo: () => 233;
declare let bar: () => number;
declare let baz: unknown;
bar = foo;
baz = bar();-
沿着返回值输出的方向,参数类型
233分配给number分配给unknown。类型分配满足向下兼容。 -
沿着函数赋值的方向,函数类型
() => 233分配给() => number。合法的分配,表现出了向下兼容。
直观的,位于返回值签名的类型参数是协变的,随着函数类型本身向着超类型分配时,他允许向着自己的超类型进行分配。
函数类型的特殊兼容
在 JavaScript 中,函数调用时可以输入比该函数形参数量更多的实参。TypeScript 的函数类型在分配时,也考虑到了这个情况,函数列表允许“前缀兼容”。
如下:
declare let foo: (a: number) => unknown;
declare let bar: (a: number, b: string) => unknown;
bar = foo;
foo = bar; // 不能向下兼容,报错了- 与逆变相似,函数参数列表的数量可以随着输入的方向变少,在该方向上向下兼容。
不严格的结构化类型
上文我们谈论过的那些不平坦的结构化类型,如记录类型,数组类型,元组类型。他们的类型参数实际上在上文被认为是协变的。
但这需要一个前提:
结构化类型所表达的值是不可变的、无状态的。
现实世界的 TypeScript 编程,可变的、有状态的结构化类型才是常态,此时的协变会带来隐藏的陷阱。
如下:
const foo: { x: number } = { x: 233 };
const trap1: { x: unknown } = foo;
trap1.x = "bad";
foo.x.toPrecision();
// ----
const bar: number[] = [233];
const trap2: unknown[] = bar;
trap2[0] = "bad";
bar[0].toPrecision();
// ----
const baz: [number] = [233];
const trap3: [unknown] = baz;
trap3[0] = "bad";
baz[0].toPrecision();-
他们的类型参数都是协变的,如
{ x: number }中属性x的类型,从number协变为unknown。 -
他们通过赋值改变部分属性的值,而且是合法的类型分配。如将
bad赋值给 属性x,类型string分配给unknown。 -
他们最终会使用被修改过的属性,调用该值的
toPrecision函数。
以上代码都能成功编译,但很显然,从上下文就能推断出代码必然报错。
实际运行中,把
string
当作
number
调用
toPrecision
函数,最终会因为
string
在装箱成
String
时缺少对应的函数而报错。
默认状态下,结构化类型在类型分配上存在缺陷,因此他是不严格的。
使结构化类型变成严格的
有两种方法使结构化类型变成严格的。
1.
readonly
在结构化类型中使用
readonly
关键字,使得类型参数都是对外输出的。此时类型参数的分配方向,始终和结构化类型的分配方向一致,语义上真正做到了协变。
如下:
const foo: { readonly x: number } = { x: 233 };
const trap1: { readonly x: unknown } = foo;
trap1.x = "bad"; // 不可赋值,报错了
foo.x.toPrecision();
// ----
const bar: readonly number[] = [233];
const trap2: readonly unknown[] = bar;
trap2[0] = "bad"; // 不可赋值,报错了
bar[0].toPrecision();
// ----
const baz: readonly [number] = [233];
const trap3: readonly [unknown] = baz;
trap3[0] = "bad"; // 不可赋值,报错了
baz[0].toPrecision();- 属性的只读阻止了他的值被修改,始终保持原来的类型。
当结构化类型所表达的值是不可变的、无状态的时候,就可以阻止赋值,从根本上避免输入不兼容类型的值。
2.
in
和
out
在泛型参数中使用
hr
ef=
"https://www.typescriptlang.org/docs/handbook/release-notes/typescript-4-7.html#optional-variance-annotations-for-type-parameters">in 或 out 关键字,使得类型参数显式带有逆变或协变的性质。此时,泛型类型的实例在分配时,相应的类型参数必须符合指定的可变性。
单独看待结构化类型的属性的赋值(输入)行为,他的类型参数的分配方向与该结构化类型的分配方向相反,应当是逆变的,因此需要标注
in
。而属性的读取(输出),显然是协变的,因此需要标注
out
。如下:
type MysteryBox<in out T> = { x: T };
const foo: MysteryBox<number> = { x: 233 };
const trap: MysteryBox<unknown> = foo; // 不可赋值,报错了
trap.x = "bad";
foo.x.toPrecision();-
由于泛型参数
T要求同时具备逆变(in)和协变(out)的性质,只有不变化才能同时满足这两点。这种不变化又称抗变。 -
由于
T的抗变,MysteryBox<number>不能分配给MysteryBox<unknown>。
当结构化类型根据他的属性用途显式标注他的可变性时,就能在类型进行分配或者说转换时,提前让编译器暴露类型不兼容的错误。
可惜,直到 TypeScript 4.8.4 的现在,可变性标注的使用仍有非常多的限制,此处不表。目前比较实用的用途是,规范泛型 class 的类型兼容,避免掉入类型兼容的陷阱。
接下来
其实到这里,本文已经谈论了 TypeScript 非常大的一部分跟类型操作相关的内容。接下来读者可以去了解如何对泛型类型和条件类型进行复合的运用,如嵌套的,递归的表达等。篇幅有限,不再展开。
一些经验之谈
关于条件类型,我还有一些想法不吐不快。
为什么条件类型表达式“无用”的分支总是返回 never ?
为什么条件类型表达式“无用”的分支总是返回
never
?上文关于
infer
的举例也是这样,返回
unknown
表示未知的类型可以吗?
因为条件类型的分配律呀。如果条件类型呈现分配律就会对“中间结果”做联合运算(
|
),而任何类型与
never
联合,如同任何集合与空集合并,得到的是该类型本身。这样一来,条件类型呈现分配律时,得到的“中间结果”为
never
的项将会被“忽略”。
如果不是刻意避免,条件类型很容易就带有分配律性质,此时对“无用”的分支返回
never
是一个不容易出错且合乎直观的选择。
值得一提的是,
Utility Types
就有一些条件类型利用了
never
完成对联合类型的“缩小/具体化”。如下:
type Exclude<T, U> = T extends U ? never : T;
type Extract<T, U> = T extends U ? T : never;
那么,如果发生在递归的条件类型中,总是对最终结果做交叉运算时,“无用”的分支返回
unknown
也许是更合适的选择。
当一些特殊的类型遇到条件类型分配律
条件类型分配律有几处奇怪的地方。
never
当条件类型能够呈现分配律时,输入
never
总会输出
never
。
如下:
type Orthrus1<T> = T extends never ? true : false;
type Orthrus2<T> = never extends T ? true : false;
type Foo = Orthrus1<never>; // type Foo = never
type Bar = Orthrus2<never>; // type Bar = true-
Foo既不是第一条分支的true,也不是第二条分支的false,而是never。
any
当条件类型能够呈现分配律时,输入
any
能同时联合两条分支的结果。
如下:
type Orthrus<T> = T extends 233 ? 22 : 33;
type Foo = Orthrus<any>; // type Foo = 22 | 33判断两个结构化类型是否相等的条件类型
上文已经出现过判断两个结构化类型相等的方法:
当两个集合互为子集时,两个集合相等。同样的, 当两个类型互为子类型时,也就是相互向下兼容时,两个类型相等 。
如果据此构造出条件类型
Equal<A, B>
,并抑制条件类型分布律。那么就能得到:
type Equal<A, B> = [A] extends [B] ? ([B] extends [A] ? true : false) : false;
目前的 TypeScript 对类型进行
|
或
&
,不总是得到最终的类型,而是显示成联合类型或交叉类型的表达式。
如下:
type Foo = { a: unknown; b: string } & { a: number };
type Bar = [number] & [unknown];
type Baz = { a: number } | { a: unknown };
type Qux = [number] | [unknown];
但有了
Equal<A, B>
就能方便地测试这些结构化类型是否与预期的类型相等。如下:
type Equal<A, B> = [A] extends [B] ? ([B] extends [A] ? true : false) : false;
type Foo = Equal<
{ a: unknown; b: string } & { a: number },
{ a: number; b: string }
>; // type Foo = true
