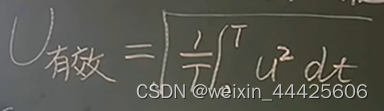逆变电路原理(直流电是怎么变成交流电的)：
逆变电路如图所示：

该电路有两种工作状态：
①第一种是S1、S4导通，电路回路如下图所示

此时，负载两端电压上+下-，电流从上到下流经负载。
②第二种是S2、S3导通，电路回路如下图所示

此时，负载两端电压上-下+，电流从下到上流经负载。

逆变输出电压表达式 ：
Uo=(4 Edc)/pi (sinwt+1/3 sin3wt+1/5 sin5wt+1/7 sin7wt…)

① ：改变负载，从0.01->0.1->1->10->100，发现负载变化，负载两端电压变化，与公式不符，因为公式中输出电压与负载阻值无关；
原因 ：整个回路是负载和2个Mosfet内阻串联分压。当负载太小(相对于Mosfet内阻而言)，Mosfet压降就会变大。一般而言，逆变输出电压与输出负载电阻无关是因为默认了负载远大于Mosfet内阻。

② ：开关管导通时间对逆变输出电压的值有影响；
原因 ：输出有效值是算积分，导通时间短，为0的时间就越多，积分的值就越小，改变频率对输出电压无影响，只要整个周期都导通，输出电压就近似等于输入电压。

③ ：负载为电阻时，电压、电流同相位；若含有电感，电压超前电流。

即方波等效成奇次正弦谐波之和，没有偶次正弦谐波，也没有余弦谐波?
傅里叶变换 ：
能将满足狄利克雷条件的某个函数(周期T)表示成三角函数(正弦/余弦或它们的线性组合).
狄利克雷条件 ： ① 在一个周期内，连续或只有有限个第一类间断点
② 在一个周期内的极大极小值是有限的
③ 在一个周期内，信号绝对可积
即满足狄利克雷信号的任何周期信号都可以表示为下图的f(t)：

接下来证明：为什么方波只有正弦谐波，并且只有奇次项。
这是我根据这个链接的视频学习后，推出的逆变输出方波的等效表达式
傅里叶变换学习链接：https://www.bilibili.com/video/BV1WT411J7EM/?spm_id_from=333.337.search-card.all.click&vd_source=845273a9efce603add87ad2d53be0027

信号在时域上是变化的，在频域上不变，将信号变在频域上更好处理和分析。
附上别的博主写的时域和频域。
https://blog.csdn.net/bocai_xiaodaidai/article/details/90765529?ops_request_misc=&request_id=&biz_id=102&utm_term=%E9%A2%91%E5%9F%9F%E6%97%B6%E5%9F%9F&utm_medium=distribute.pc_search_result.none-task-blog-2 _all sobaiduweb~default-0-90765529.142 ^v88 control_2,239 ^v2 insert_chatgpt&spm=1018.2226.3001.4187
为什么要将时域变换到频域？
比如某些场合，如电路分析，我们常常习惯将电路中的器件表达成关于角频率w的等效阻抗的表达式，电容=1/jwC，电感=jwL，所以也需要将电源转换成频域，让整个电路在同一个域下分析。当然也可以不对电源做变换，让电源仍然是时间t的表达式，然后将电路元件C、L写成时间t的表达式，进行时域分析。 但在频域下使用交流阻抗分析法是分析电路最常用的方法。


图1是正弦波的时域图，示出了振幅与时间的关系。
图2是图1中正弦波的频域图

这里首先介绍几种值的定义：
平均值 ：一个周期内，信号的等效值

有效值 ：焦耳定理定义AC信号等效为DC信号的值

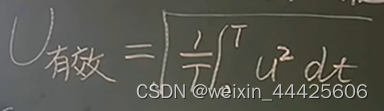
均方根值 ：(RMS,real mean sqare)；数学上定义AC信号等效为DC信号的值
对于AC信号而言，均方根值和有效值是一个东西
紧接着讨论 为什么方波有效电压U不等于各个谐波有效电压之和 ，即U≠2 √2U/pi+2 √2 U/(1 pi/3)+2 √2 U/(1*pi/5)+…(U≠0.9U+0.3U+…)， 但我们还是用各个谐波电压作用于电路的结果之和等效于方波作用于电路 。
能量是始终守恒 的， 不同频的信号不能直接叠加计算电压有效值，应该计算他们作用在负载上的总功率值 。即
U**2=(0.9U)**2+(0.3U)**2+…
通过仿真也可以验证上述观点

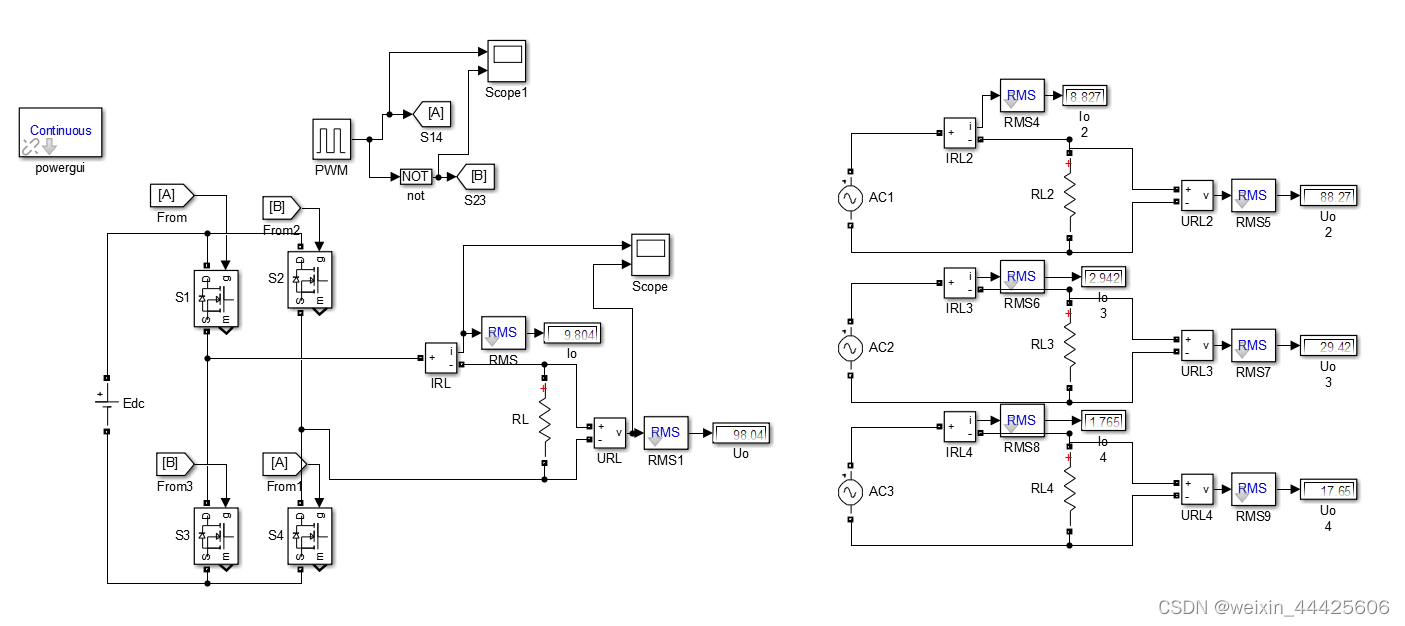
Edc=100V,逆变输出方波98.04V，RL=RL2=RL3=RL410Ω，
AC1的peak ampititude=4 98.04/(1 pi)，frequency=100e3;AC2的peak ampititude=4 98.04/(3 pi)，frequency=300e3;AC3的peak ampititude=4 98.04/(5 pi)，frequency=500e3;…
用方波作为电压作用于10Ω的负载时的功率=用各个奇次正弦谐波作用于10Ω的负载的功率之和。
方波输出电压有效值≠各个奇次正弦谐波电压有效值之和；方波输出电流有效值≠各个奇次正弦谐波电流有效值之和