卡尔曼滤波器--基础知识及公式推导

一、卡尔曼滤波器的应用场景

卡尔曼滤波器之前被广泛用来做动态系统的状态估计、预测。主要的目的就是用来从带噪声的观测量，比如各种传感器的观测（IMU、GPS、里程计等）估计出最优的系统状态（state）。不过要明确强调的是，由于测量都带有噪声，也就是随机性，所以真正准确的状态是无法获知的。

最小二乘法可以从一长串的测量值回归出一个最为匹配的模型。卡尔曼滤波相比于最小二乘法，采用了一种递归的计算方式，也就是每一时刻只需要保存上一时刻的状态。因此可以被用来处理实时任务。

应用得较广的例子：

如何从IMU的数据（三轴加速度，三轴角速度）计算出运动物体的当前位置。

二、卡尔曼滤波的两个步骤——宏观认识

卡尔曼滤波包含两个步骤

1. 预测（prediction）—— Dynamic model
2. 更新（correction/measurment update）—— Observation model

所谓【预测】，就是用一个数学模型，根据当前的传感器输入，直接计算此时系统的状态。可以理解为一个方程的计算就行。

所谓的【更新】，就是在某些时刻或者每一时刻，获取一些系统的状态输入（可以同样是传感器的值），甚至是【预测】阶段中的同样的传感器的值，将其当作带噪声的真值，我们将这个值叫做【测量值】。比较此刻【预测】的系统状态和【测量】的系统状态，对【预测】的系统状态进行修正。因此也叫测量更新（measurment update）

三、卡尔曼滤波的几大概念

1、状态向量State Vector

系统的状态向量包含了系统中我们关心的状态变量，比如速度 \textbf{v}=[v_x, v_y,v_z] ，距离 \textbf{d}=[d_x, d_y,d_z] ；加速度 \textbf{a}=[a_x,a_y,a_z] 。我们用 \textbf{x} 表示系统向量

\textbf{x} = \begin{bmatrix} \textbf{d}\\ \textbf{v}\\ \textbf{a} \end{bmatrix}\\ 因为卡尔曼滤波有两个步骤，我们先以每个时刻都进行测量和修正这两个步骤都作为讲解。那么，每一时刻的两个步骤的输出对应两个系统向量，一个是预测的系统向量 \textbf{x}^- (priori value)，一个是修正后的系统向量 \textbf{x}^+ .

PS:大写字母表示矩阵；小写加粗字母表示向量；小写字母表示变量

2、状态方程&&预测方程

状态方程 描述了将上一时刻的状态向量 \textbf{x}_{t-1} 映射到当前的系统状态 \textbf{x}_t

\textbf{x}_t = \textbf{A}_t\textbf{x}_{t-1}+ \textbf{B}_t\textbf{u}_t+w_t \tag{1}\\ 其中，矩阵 \textbf{A} 称为转换矩阵（Transition Matrix）， \textbf{u}_t 是当前时刻的系统输入，矩阵 \textbf{B} 称为控制矩阵（Control Matrix）反映了系统输入到系统状态的映射关系， w_t 是过程噪声，我们假定其符合均值为0，协方差矩阵为 Q_t 的高斯噪声。这里要注意的有几点：

1. A、B都随着时间演进进行更新
2. 从公式1的形式也可以看出，卡尔曼滤波的数学建模形式是线性方程，这也是卡尔曼滤波的限制之一。扩展卡尔曼滤波器（Extended Kalman Filter）支持非线性模型。
3. 这里的状态方程是一个“准确”的表达，因为不准确的部分已经放在噪声 w_t 中，要跟预测方程区分开来。但是这个完全准确的表达由于有噪声（随机向量），所以我们没办法使用它作为输出，只能用它来分析、推导。

预测方程 跟状态方程基本一样，要强调的一点是，噪声 w_t 是均值为0的高斯噪声，因此最大概率对应的值为0，因此我们在预测状态向量计算的时候其实不用管最后一项

\hat{\textbf{x}}^-_t = \textbf{A}_t\hat{\textbf{x}}^+_{t-1} + \textbf{B}_t\textbf{u}_t\tag{2}\\

这里对系统状态向量上面加上一个帽子表示这是一个估计量，也就是我们实际输出的量。其中 \hat{\textbf{x}}^+ _{t-1} 表示上一时刻执行完步骤二【更新】后的状态向量， \hat{\textbf{x}}^- _{t} 表示当前时候只执行了步骤1【预测】的状态向量。

3、测量方程&&测量更新方程

测量方程 反映了系统的测量值和系统状态向量之间的关系

\textbf{z}_t=H_t\textbf{x}_t+\textbf{v}_t\tag{3}\\ 其中， \textbf{z}_t 是当前时刻的测量值， \textbf{H}_t 称为测量矩阵（Measurement Matrix），描述了从系统状态到测量值的转换关系（举一个最简单的关系，系统状态是物体的直线距离，测量值是使用激光笔测出来的光从原点到物体的时间，那么H就是光速的倒数）, \textbf{v}_t 是测量噪声，我们假定其符合均值为0，协方差为 R_t 的高斯噪声。注意这里无论是状态向量还是测量向量都没有加帽子（ \hat{} ），表示这是个准确的表达式，噪声项在 v_t 中。

测量更新方程： 同样，我们如果忽略噪声项，就变成了对此时测量量的估计（注意状态向量的上标和角标）：

\hat{\textbf{z}}_t=H_t\hat{\textbf{x}}^-_t\tag{4}\\

4、测量更新方程

上面给出了对测量量的估计，但是现在的情况是，我们有了一个测量值（通过某些测量方式或者传感器数据），是一个不需要计算得到的量，我们如何用这个测量得出的量来更新我们对状态向量的估计？这就涉及到测量更新方程，这也是卡尔曼滤波里最难的部分，这里先给出更新方程的形式。

\hat{\textbf{x}}^+_t=\hat{\textbf{x}}^-_t+K_t(z_t-H_t\hat{\textbf{x}}^-_t)\tag{5}\\ K_t=\frac{P^-_tH_t^T}{H_tP^-_tH_t^T+R_t}\tag{6}\\

其中， K_t 叫做卡尔曼增益； P^-_t 是系统测量值 \hat{\textbf{x}}^-_t 的 误差 协方差矩阵

四、误差和协方差矩阵

根据公式（1）减去公式（2），我们可以得出误差的协方差矩阵的表达形式

e^-_t \triangleq \textbf{x}_t - \hat{\textbf{x}}^-_t\\ P^-_t = \mathbb{E}[\textbf{e}^-_t {\textbf{e}^{-}_{t}}^T]\\

把公式（1）和（2）带入误差表达式，可以推导出系统状态的协方差矩阵的递归表达形式

\begin{align}P^-_t&=\mathbb{E}[\big((A_tx_{t-1}+w_t)-A_tx_{t-1}^+\big)\big((A_tx_{t-1}+w_t)-A_tx_{t-1}^+\big)^T]\\ &=\mathbb{E}[\big(A_t(x_{t-1}-x_{t-1}^+)+w_t\big)\big(A_t(x_{t-1}-x_{t-1}^+)+w_t\big)^T]\\ &=\mathbb{E}[A_t(x_{t-1}-x_{t-1}^+)(x_{t-1}-x_{t-1}^+)^TA_t^T]+\mathbb{E}[w_tw_t^T]\\ &=A_tP_{t-1}^+A_t^T+Q_t \end{align} \\ 其中，从第二个等号到第三个等号利用了状态向量和随机噪声 w_t 的无关性（协方差为0）。因此我们可以得到下面的公式（7）

P^-_t=A_tP^+_{t-1}A^T_t+Q_t\tag{7}\\

五、更新方程的推导

现在我们进行到了这样的情况，我们使用预测方程公式（2）得到了 t 时刻的系统状态预测量 \textbf{x}_t^- ；同时，我们在这个时刻得到了一个测量值，且根据测量方程，我们认为它与此时的状态向量满足公式（3）： \textbf{z}_t=H_t\textbf{x}_t+v_t 。那么其实我们可以从公式（3）也得到此时系统状态的另一个估计，由公式（3）将 x_t 移动到等式左侧，可以得到：

\textbf{x}^2_t = \textbf{H}_t^{-1}\textbf{z}_t\\ 这里只所以没有把噪声 \textbf{v}_t 表示出来，是因为这里将 \textbf{z}_t 当作一个随机向量处理，其均值为 \bar{z}_t ，也就是当前时刻测量得出的量；其方差为 R_t （在公式3中给出）

我们的状态方程也给出了状态向量的一个等式

\textbf{x}^1_t = \textbf{A}_t\textbf{x}_{t-1}+ \textbf{B}_t\textbf{u}_t+w_t \\ 这里用上标1和2表示状态向量的两个来源。要强调的是，这两个等式里面都包含了一个随机噪声，因此 \textbf{x}^1_t 、\textbf{x}^2_t 都是随机向量。同时，他们的分布都符合高斯分布（因为这里的随机噪声我们假设是高斯噪声）。它们的均值和方差分别是：

\begin{align} &\mu_1=x_t^-\\ &\sigma_1^2=P_t^-\\ &\mu_2=H_t^{-1}\bar{z}_t\\ &\sigma_2^2=H_t^{-1}R_t(H_t^{-1})^T\\ \end{align}\\ 现在有了两个关于状态向量的概率分布，那接下来的事情就简单了。因为这两个状态向量的来源我们可以认为是独立的，因此他们的联合概率分布是各自概率分布的乘积。 重点是，高斯分布的乘积依旧是高斯分布！！！！ 新的高斯分布的均值和方差有如下表达形式：

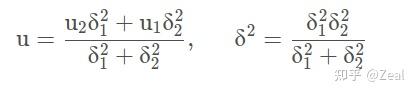
用上面的式子代入

\begin{align} \mu_{fused}&=\frac{\mu_1\sigma_2^2+\mu_2\sigma_1^2}{\sigma_1^2+\sigma_2^2}\\ &=\mu_1+\frac{(\mu_2-\mu_1)\sigma_1^2}{\sigma_1^2+\sigma_2^2}\\ &=x_t^-+\frac{(H_t^{-1}\bar{z}_t-x_t^-)P_t^-}{P_t^-+H_t^{-1}R_t(H_t^{-1})^T}\\ &=x_t^-+\frac{P_t^-H_t^T}{H_tP_t^-H_t^T+R_t}(\bar{z}_t-H_tx_t^-)\\ &=x_t^-+K_t(\bar{z}_t-H_tx_t^-) \end{align}\\ \begin{align} \sigma_{fused}^2 &=\frac{\sigma_1^2\sigma_2^2}{\sigma_1^2+\sigma_2^2}\\ &=\sigma_1^2-\frac{\sigma_1^4}{\sigma_1^2+\sigma_2^2}\\ &=P_t^--\frac{P_t^-H_t^TH_tP_t^-}{H_tP_t^-H_t^T+R_t}\\ &=P_t^--K_tH_tP_t^- \end{align}\\ 这个 \sigma_{fused}^2 就是更新后的系统状态误差的协方差矩阵，也就是得到下面的式子

P^+_{t}=P^-_t-K_tH_tP^-_t\tag{8}\\

六、总结

预测方程

\hat{\textbf{x}}^-_t = \textbf{A}_t\hat{\textbf{x}}^+_{t-1} + \textbf{B}_t\textbf{u}(t)\tag{2}\\

更新方程

\hat{\textbf{x}}^+_t=\hat{\textbf{x}}^-_t+K_t(z_t-H_t\hat{\textbf{x}}^-_t)\tag{5}\\ K_t=\frac{P^-_tH_t^T}{H_tP^-_tH_t^T+R_t}\tag{6}\\ P^+_{t}=P^-_t-K_tH_tP^-_t\tag{8}\\