-
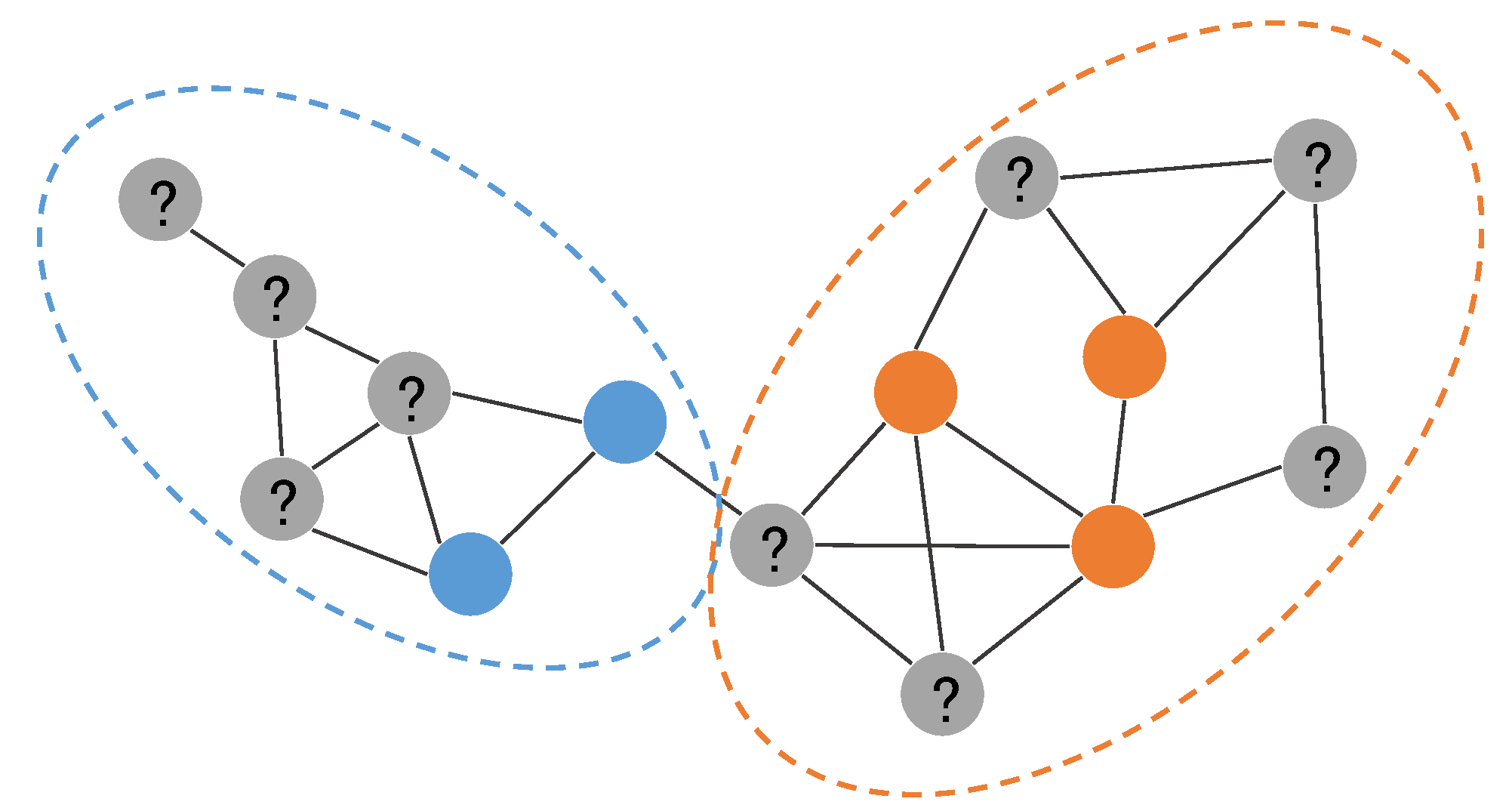
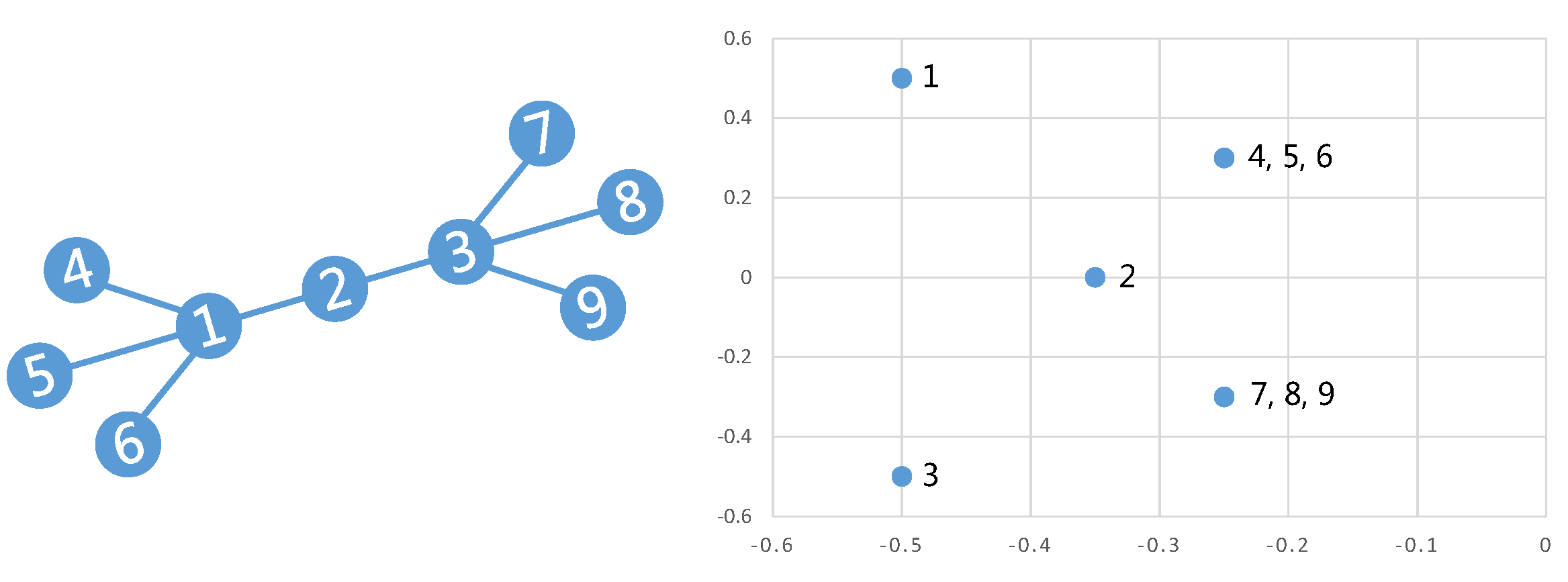
Planetoid模型:单输入双输入神经网络
-
SEANO模型:双输入双输出神经网络
-
图卷积神经网络GCN
图编码方法关注于利用邻居特征将节点编码到一个低维空间,学习节点的特征编码(feature embedding),然后基于学得的特征编码构建分类器。 用上下文训练得到的编码能够用来提高相关任务的性能。典型地,从语言模型训练的词编码可以应用于词性标注、情感分类和命名实体识别。 值得注意的是,并不是所有图编码方法都是半监督的。事实上,早期的图编码方法大多是无监督的,这些方法把编码任务和分类任务放在两个不同的模型中,先采用无监督编码学习到节点特征表示,再基于学习到的特征训练分类器。这种流水线的方式使得图编码方法广泛应用于图分析的各类任务,比如节点分类
bhagat2011node
、链接预测
liben2007link
、社团检测
cavallari2017learning
、推荐系统
yu2014personalized
和可视化
maaten2008visualizing
。但是这种方式在训练过程中缺乏有监督信息的调整,编码得到的特征不是针对类别标签的,可能使不同类别的节点在特征空间上还是难以分开。近期的一些图编码方法,将编码和分类这两个任务合并在一个统一的端到端模型中,提出半监督图编码方法。实验结果表明,在图节点分类任务上,半监督图编码只需要极少比例的标记样本就能取得不错的效果。接下来具体对这两类图编码方法进行介绍。
cao2015grarep
将节点间转移概率定义为$T = D^{-1}A$,并引入$k$阶概率转移矩阵
为了减少误差和方便计算,GraRep通过 $A^k$ 计算得到正值 $k$ 阶对数概率矩阵 $X^k$ ,并采用奇异值分解(SVD)来求解目标函数 $ \Vert X^k - H^k_i H^k_j \Vert^2_F $ ,得到$k$阶特征编码。最后将所有$H^k_i$合并得到节点$v_i$的最终编码$H_i$。
HOPE
ou2016asymmetric
采用了相似的目标函数来保持高阶近似,$ \Vert S - H_i H_j\Vert^2_F $。 $S$为相似度矩阵,通过对其的计算来保持高阶近似。HOPE采用了一些流行的近似度度量方法进行实验。它发现图中的许多高阶邻近度量可以反映不对称传递性,此外,它们大多共享一个通用公式,这将有助于近似这些近似值:$S = M_g^{-1} \cdot M_l$,其中$M_g$和$ M_l$都是稀疏矩阵。这使得HOPE能够利用广义奇异值分解来有效的求解并得到编码结果。
受word2vec
mikolov2013distributed
成功的影响,目前越来越多的研究关注于利用类似skip-gram的模型来做图编码。Skip-gram是一种softmax的变种,给定一个样本和其上下文,skip-gram的目标通常是最小化预测上下文的log损失,其中预测上下文利用的是样本的编码作为输入。具体地,设${(i,c)}$是样本$i$和其上下文$c$的组合对的集合,log损失函数能写成:
其中,$\mathcal{C}$是所有可能上下文的集合,$w$是模型参数,$e_i$是样本$i$的编码。Skip-gram模型最开始用于学习词的向量表示,也就是word2vec。在word2vec中,每个训练对$(i,c)$,表示此时要去估计样本$i$的编码,上下文 $c$ 是词$i$在序列中给定窗口内的词,上下文集合空间$\mathcal{C}$为语料库中所有的词。目前许多基于随机游走的方法采用skip-gram模型来学习图节点编码。DeepWalk
perozzi2014deepwalk
使用节点的编码来预测其在图中的上下文,其上下文是通过随机游走生成的。对于每个训练对$(i,c)$,样本$i$为当前节点,$c$为样本$i$在一定窗口大小的邻居中采用随机游走采样生成的序列,也就是说c的长度是固定的,为窗口的大小。LINE
tang2015line
扩展了DeepWalk,使其具备多个上下文空间$\mathcal{C}$,用于建模一阶和二阶近似。Node2vec
grover2016node2vec
采用带偏置的随机游走,在宽度优先(BFS)和深度优先(DFS)搜索之间提供权衡,因此可生成比DeepWalk更高质量和更丰富信息的编码。选择合适的平衡可以使node2vec保留社区结构以及节点之间的结构对等性。
虽然类似skip-gram的模型最近获取了很大的关注,其他神经网络上的方法同样也被扩展到图的编码中来,比如自动编码机(Autoencoder)。自动编码机是一种典型的无监督神经网络,主要用于高维数据降维和特征学习,已经在各种各样的实际问题中得到了广泛的应用。SDNE(Structural Deep Network Embedding)
wang2016structural
采用自动编码机来对网络中节点进行编码。

在SDNE中,$x_i = A_i$为邻接矩阵$A$的第$i$行,反映节点$v_i$的网络结构向量。通过在$x_i$上施行自动编码机,使得学到的编码$h_i = y_i^{(K)}$能够保持高阶依赖。因为自动编码机约束输出$\widehat{x_i}$与输入$x_i$一致,这使得编码$h_i$能够推理节点的上下文(网络连接关系),从而保持高阶依赖。不难看出,SDNE在一般自动编码机的基础上,加上了网络结构的约束。这里采用的约束是之前介绍的拉普拉斯特征映射(Laplacian Eigenmaps),约束网络上相近的节点有相近的编码结果。因此,SDNE能同时保持一阶近似和高阶近似,其损失函数为:
其中$\mathcal{L}_{2nd}$对原始的自动编码机的损失做了一定修改,引入惩罚项$B$, 对非零元素的重构误差施加了比零元素更多的惩罚,使得模型更容易重构$X$中的1而不是0。对于$B$,SDNE的定义为:如果 $A
{ij} = 0$,$b
{ij} = 1$,否则$b_{ij} = \beta > 1$。设计B的出发点是,有边相连表示两点相似,但是没有边相连,不一定代表其不相似。这样一来就能重构高阶邻居的结构信息。 与SDNE直接在邻接矩阵上施行自动编码机不同的是,DNGR
cao2016deep
结合了随机游走和自动编码机来完成图编码。DNGR首先利用随机游走方法生成带有高阶图结构信息的表达矩阵,然后计算PPMI(positive pointwise mutual information,一种词向量表达方式)矩阵,最后在PPMI矩阵的基础上利用自动编码机替换SVD得到最终的编码结果。
以上第一类无监督图编码方法在编码过程中没有用到节点的特征属性,只编码了网络结构。然而,在实际中,网络中节点往往拥有丰富的信息,比如社交网络中用户发布的微博内容。节点的特征属性更准确的反映了节点的信息,这对于节点的分类任务尤为重要。TADW
yang2015network
认识到这一点,同时将网络结构和节点特征进行编码。TADW证明了DeepWalk本质上等同于矩阵分解,并在矩阵分解的框架下将节点的文本特征合并到网络表示学习中。
以上无监督图编码方法固然有其普适性等优点,但在图节点分类任务上,它们并没有将节点的标签信息用作编码,而且分类器的训练是在编码的学习之后。所以编码的结果并不是针对该特定的任务的,这也导致该类方法在图节点分类任务上并未达到最先进的结果。
yang2016revisiting
为图中每个节点训练一个特征编码来联合预测图中的类别标签和邻域上下文。具体地,Planetoid提出了直推(transductive)和归纳(inductive)两种形式的半监督模型,前者假定学习过程中所考虑的未标记样本是待预测数据(图中已观测到的节点,基于“封闭世界”),学习的目的就是在这些未标记样本上获得最优泛化性能,而后者假定训练数据中的未标记样本并非仅仅是待预测数据(包括未观测的节点,基于“开放世界”)。下图给出了这两种方式的网络结构。
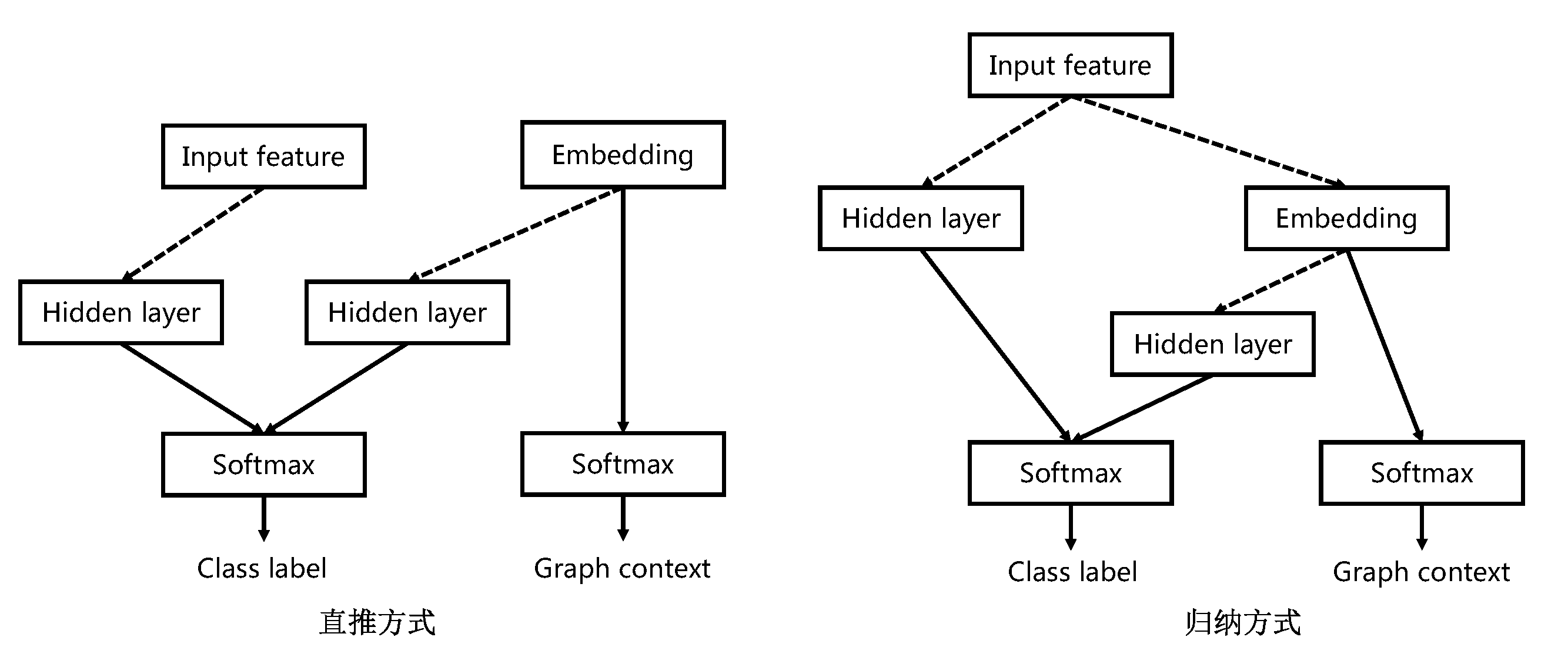
图中直线箭头表示直接相连,虚线箭头表示一个或者多个前馈层。在直推方式中,类别标签由学习的编码和输入的特征向量同时决定。但是在归纳方式中,未标记样本的编码并不能提前学习到,只有在图中观测到的节点才能学习到,因此归纳方式对直推方式的结构做了点修改,将编码定义为特征向量的的参数化函数并且类别标签只依赖于特征向量,这样便可以对训练中未观测到的样本做出预测。
SEANO
liang2017seano
拥有相似的模型结构,不同的是SEANO设计了一个双输入双输出深度神经网络来归纳学习节点编码。其网络结构见下图。
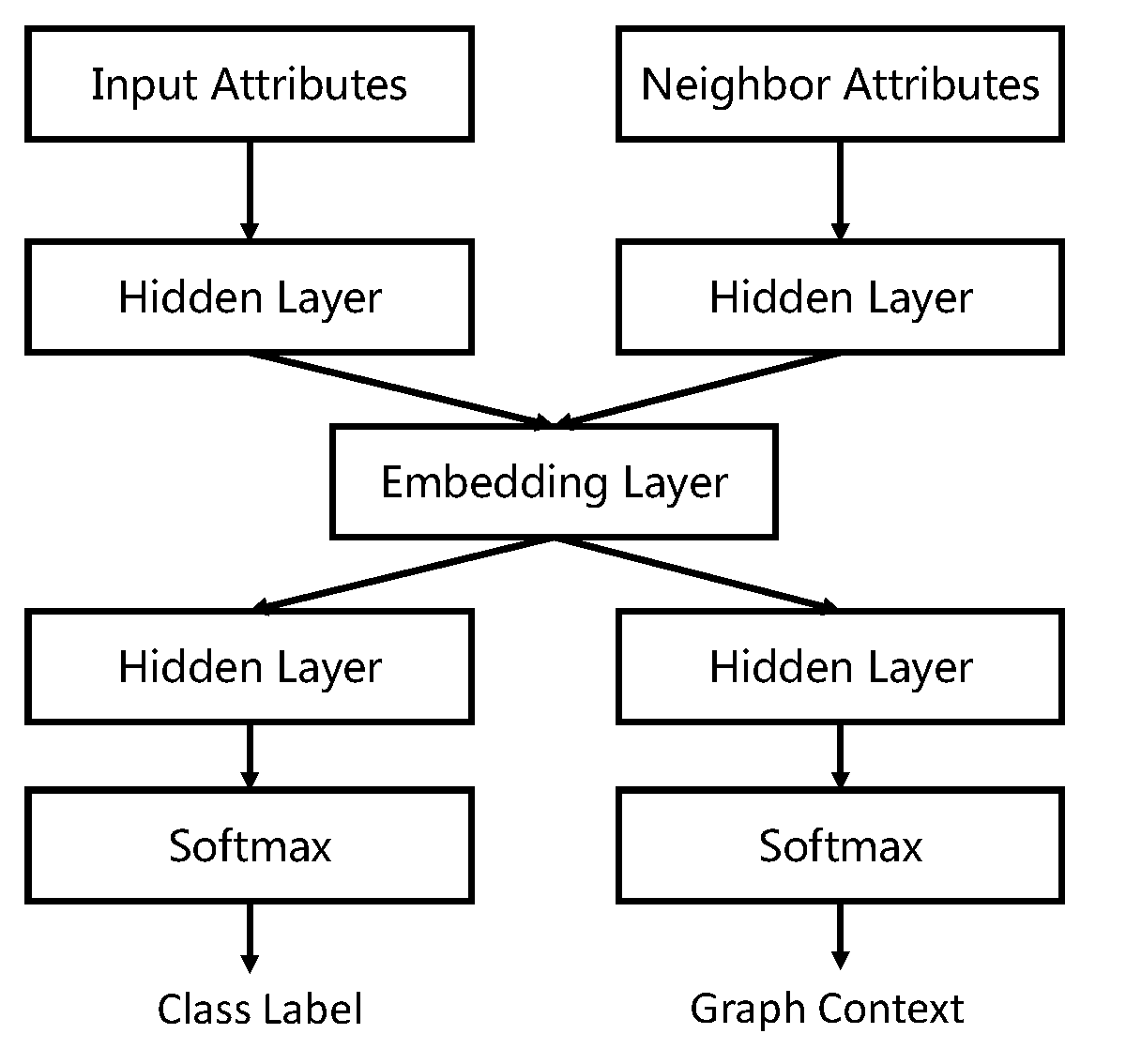
在这里,输入不仅仅是当前节点的特征,还有该节点邻居的特征的加权求和。他们通过相同的一组非线性映射函数,并通过加权求和在编码中进行聚合。 图中的左输出层预测输入节点的类标签,而右输出层产生网络输入的上下文,两者通过共享编码层使得得到的编码能捕获节点特征、网络结构和类别标签三个方面的信息。但是这里有两个输出层,需要分步进行调整,对模型的训练造成了一定不便。
借鉴卷积神经网络的思想,将节点周围的一阶邻居看成其感受野,GCN
kipf2016semi
提出了一种直接在图上操作的卷积神经网络的有效变体。这是一种简单有效的基于神经网络的分层传播规则。GCN的核心是其卷积方式,具体的卷积过程为:
其中$W^{l}$ 为第$l$层的模型参数,$H^{l}$为第$l$层的输出,$\widehat{A}$的为采用了再归一化技巧后的图拉普拉斯矩阵。具体地,$ \widehat{A} = \widetilde{D}^{ -\frac{1}{2} } \widetilde{A} \widetilde{D}^{ -\frac{1}{2} }$, 其中,$\widetilde{A} = A + I
N $,$\widetilde{D}\
{ii} = \sum
j \widetilde{A}
{ij}$。 该卷积将每个点的特征变换成了自己和邻居的特征的加权求和,即$\widehat{A}X$。由于$\widehat{A}$中所有元素的值都小于1,$\widehat{A} X$ 的意义就是在特征空间上节点向其邻居所在的方向加权移动。理想情况下,如果一个节点特征不好分,但是其邻居都远离分界面,那么该点向邻居的移动会使其远离分界面,变得可分。所以$\widehat{A} X$ 使得节点的特征与邻居的特征的差异性一定程度减小,也就是做了局部平滑。基于上式,GCN提出了一个两层的半监督神经网络模型:
第一层用来做编码,第二层用来做分类。相比于SEANO,GCN更加简单有效而且同时利用了部分标记的标签和网络结构。
值得注意的是,GCN只需要少量的标记样本就能在整个网络上取得很好的分类结果。
miller1997separators
. MILLER G L, TENG S H, THURSTON W, et al., 1997. Separators for sphere-packings and nearest neighbor graphs[J]. Journal of the ACM (JACM), 44(1): 1–29.
↩
dong2011efficient
. DONG W, MOSES C, LI K, 2011. Efficient k-nearest neighbor graph construction for generic similarity measures[C]//Proceedings of the 20th international conference on World wide web. ACM: 577–586.
↩
zhang2013fast
. ZHANG Y M, HUANG K, GENG G, et al., 2013. Fast knn graph construction with locality sensitive hashing[C]//Joint European Conference on Machine Learning and Knowledge Discovery in Databases. Springer: 660–674.
↩
bhagat2011node
. BHAGAT S, CORMODE G, MUTHUKRISHNAN S, 2011. Node classification in social networks[M]//Social network data analytics. Springer: 115–148.
↩
liben2007link
. LIBEN-NOWELL D, KLEINBERG J, 2007. The link-prediction problem for social networks[J]. journal of the Association for Information Science and Technology, 58(7): 1019–1031.
↩
cavallari2017learning
. CAVALLARI S, ZHENG V W, CAI H, et al., 2017. Learning community embedding with community detection and node embedding on graphs[C]//Proceedings of the 2017 ACM on Conference on Information and Knowledge Management. ACM: 377–386.
↩
yu2014personalized
. YU X, REN X, SUN Y, et al., 2014. Personalized entity recommendation: A heterogeneous information network approach[C]//Proceedings of the 7th ACM international conference on Web search and data mining. ACM: 283–292.
↩
maaten2008visualizing
. MAATEN L V D, HINTON G, 2008. Visualizing data using t-sne[J]. Journal of machine learning research, 9(Nov): 2579–2605.
↩
cao2015grarep
. CAO S, LU W, XU Q, 2015. Grarep: Learning graph representations with global structural information[C]//Proceedings of the 24th ACM International on Conference on Information and Knowledge Management. ACM: 891–900.
↩
ou2016asymmetric
. OU M, CUI P, PEI J, et al., 2016. Asymmetric transitivity preserving graph embedding[C]//Proceedings of the 22nd ACM SIGKDD international conference on Knowledge discovery and data mining. ACM: 1105–1114.
↩
mikolov2013distributed
. MIKOLOV T, SUTSKEVER I, CHEN K, et al., 2013. Distributed representations of words and phrases and their compositionality[J]. neural information processing systems: 3111–3119.
↩
dash2008context
. DASH N S, 2008. Context and contextual word meaning.[J]. SKASE Journal of Theoretical Linguistics.
↩
jin2001structure
. JIN E M, GIRVAN M, NEWMAN M E, 2001. Structure of growing social networks[J]. Physical review E, 64(4): 046132.
↩
zhu2002learning
. ZHU X, GHAHRAMANI Z, 2002. Learning from labeled and unlabeled data with label propagation[Z]. Citeseer
↩
zhu2003semi
. ZHU X, GHAHRAMANI Z, LAFFERTY J D, 2003. Semi-supervised learning using gaussian fields and harmonic functions[C]//Proceedings of the 20th International conference on Machine learning (ICML-03). 912–919.
↩
belkin2006manifold
. BELKIN M, NIYOGI P, SINDHWANI V, 2006. Manifold regularization: A geometric framework for learning from labeled and unlabeled examples[J]. Journal of machine learning research, 7(Nov): 2399–2434.
↩
lu2003link
. LU Q, GETOOR L, 2003. Link-based classification[C]//Proceedings of the 20th International Conference on Machine Learning (ICML-03). 496–503.
↩
perozzi2014deepwalk
. PEROZZI B, AL-RFOU R, SKIENA S, 2014. Deepwalk: Online learning of social representations [C]//Proceedings of the 20th ACM SIGKDD international conference on Knowledge discovery and data mining. ACM: 701–710.
↩
tang2015line
. TANG J, QU M, WANG M, et al., 2015. Line: Large-scale information network embedding[C]//Proceedings of the 24th International Conference on World Wide Web. [S.l.]: International World Wide Web Conferences Steering Committee: 1067–1077.
↩
grover2016node2vec
. GROVER A, LESKOVEC J, 2016. node2vec: Scalable feature learning for networks[C]//Proceedings of the 22nd ACM SIGKDD international conference on Knowledge discovery and data mining. ACM: 855–864.
↩
wang2016structural
. WANG D, CUI P, ZHU W, 2016. Structural deep network embedding[C]//Proceedings of the 22nd ACM SIGKDD international conference on Knowledge discovery and data mining. ACM: 1225–1234.
↩
cao2016deep
. CAO S, LU W, XU Q, 2016. Deep neural networks for learning graph representations.[C]//AAAI. 1145–1152.
↩
yang2015network
. YANG C, LIU Z, ZHAO D, et al., 2015. Network representation learning with rich text information. [C]//IJCAI. 2111–2117.
↩
yang2016revisiting
. YANG Z, COHEN W W, SALAKHUTDINOV R, 2016a. Revisiting semi-supervised learning with graph embeddings[J]. arXiv preprint arXiv:1603.08861.
↩
liang2017seano
. LIANG J, JACOBS P, PARTHASARATHY S, 2017. Seano: semi-supervised embedding in attributed networks with outliers[J]. arXiv preprint arXiv:1703.08100.
↩
kipf2016semi
. KIPF T N, WELLING M, 2016. Semi-supervised classification with graph convolutional networks[J]. arXiv preprint arXiv:1609.02907.
↩