时间序列:多步预测的方法以及序列问题的分类


1 单步预测与多步预测
单步预测: 输入全部真实值,仅预测未来一个值。
多步预测: 预测多个未来值,可以是一次性预测多个未来值,也可以是进行多次预测得到多个未来值。
在时间序列预测中,进行建模的时候我们面临最直接的问题就是时间窗的问题——即我们要用多少时间步的历史数据,去预测多少个时间步的未来数据。
除此之外,还有一个gap的问题,也就是提前多少天预测。实际的应用的时候,经常需要做提前预测,例如我们可能需要在11月1日预测11月11日,则就是提前10天做预测,那么进行特征构建的时候也需要注意,滞后特征要从10天前开始做起。
我们很少做真正意义上的多步预测——一次性预测多个,因为这样的预测效果往往很糟糕。但有不少方法,可以提供将多步预测转为单步预测,依然实现对未来多个值的预测。
1.1 【方法1】直接法 Direct
本质上就是单步预测,只不过如果我要预测未来n个值,就构建n个模型进行n次预测。
举个例子,有10天的真实数据,需要预测第11、12、13天。在特征工程里,有一种滞后特征。我们可以构造1阶滞后特征[NA,1,2,3,4,5,6,7,8,9]来预测第11个,构造2阶滞后特征[NA,NA,1,2,3,4,5,6,7,8]来预测第12个,以此类推……这就是滑动窗口。
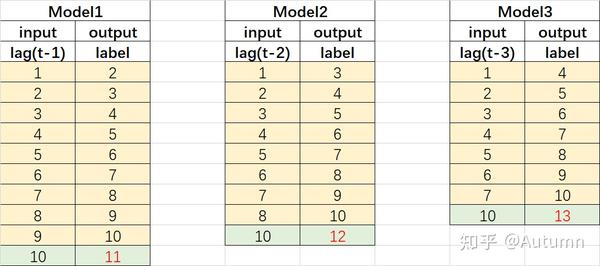
1.2 【方法2】滚动法/递归法 Recursive
这个方法不需要n个模型,仅需1个模型就可以预测n个值。原因在于,输入的原始数据为真实值,但每预测完一个值,都会将这个预测值作为新的特征,来预测下一个值。
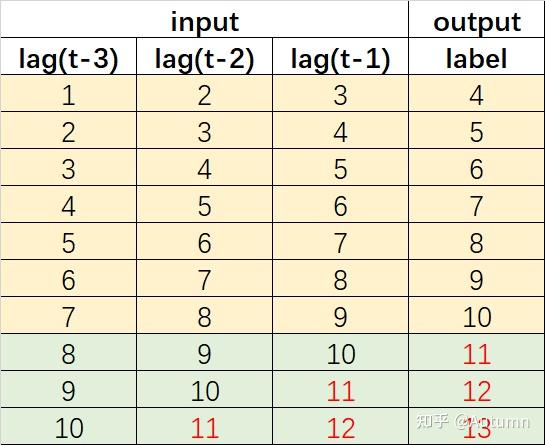
这也是ARIMA模型或者指数平滑预测模型采用的方法。
但是由于使用预测代替真实值,递归策略会累积预测误差,所以随着预测时间范围的增加,模型的性能可能会迅速下降。
1.3 【方法3】直接法+递归法 DirRec
和直接预测一样我们要根据预测的n个时间步构造n个模型(这n个模型可以是一样的结构也可以是不一样的结构),但不同的是,每一个预测值都会作为输入值参与后续其他模型的训练。
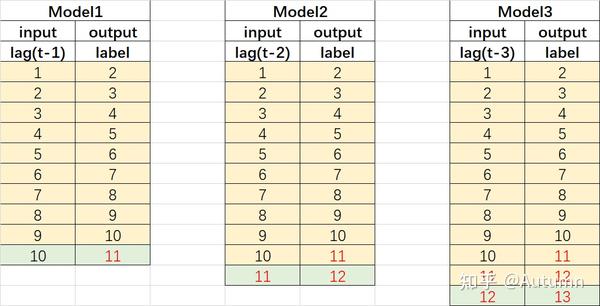
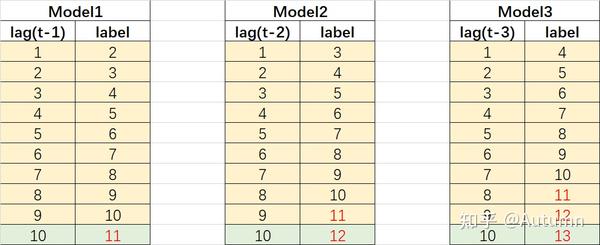
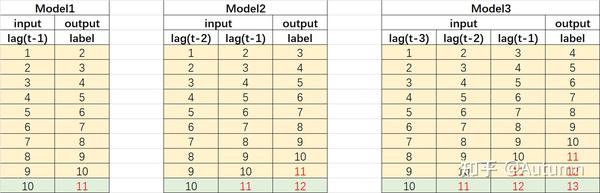
直接预测和滚动/迭代预测方法,就是常见的使用传统的机器学习算法解决多标签(多输出)问题的转化方法,本质上还是单标签问题。
以上方法都不是单纯的多步预测,如果要直接用多个真实值一次性输出多个预测值,传统的机器学习算法是无法正常处理的。
1.4 【方法4】多输入多输出法 MIMO(multiple input multiple output)
多步预测的本质是多输出,要想在一个模型里预测多个标签,就需要“多输出模型”。在这里,返回的不是一个标量,而是一个序列。
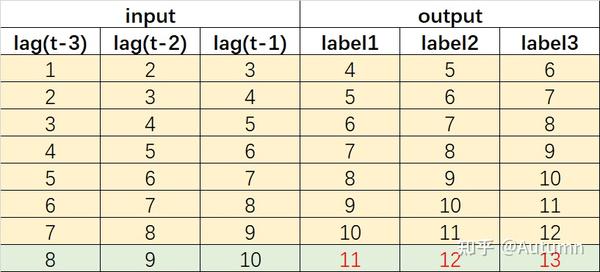
和直接策略相比,MIMO只使用一个多输出模型,保留了隐藏在预测时间序列中的时间随机依赖性。该策略也避免了递归法所面临的误差累积。
但是MIMO法有一个缺点,它限制了所有的同一样本的预测值都要用相同的模型结构进行预测,例如用相同的输入集,并使用相同的学习程序。这种约束大大降低了灵活性和可变性,并可能产生偏离返回模型的负面效果。
2 one to one, one to many, many to one 以及 many to many
时间序列预测是指我们必须基于时间相关输入预测结果的问题类型。时间序列数据的一个典型示例是股票市场数据,其中股票价格随时间变化。类似地,特定地点的每小时温度也会发生变化,也可以视为时间序列数据。时间序列数据基本上是一个数据序列, 因此时间序列问题通常被称为序列问题 。
序列问题可以大致分为以下几类:
- one to one 一对一
- one to many 一对多
- many to one 多对一
- many to many 多对多
RNN常被用来解决序列问题,LSTM(RNN变体)则更适合解决长序列问题。在进行LSTM模型训练的时候,我们通常要将数据集转换为tensor(张量,在R语言中和array类似),因为PyTorch模型是使用tensor进行训练的。
2.1 张量 tensor
张量的维度可以有很多个,在构建LSTM训练数据集时,一般用的是三个维度
tensor(a,b,c)
,其中
a
表示samples,代表样本数;
b
表示time steps,代表时间步;
c
表示features或者labels,代表特征数或者标签数。

上面这个例子表明:一共有3个样本,每个样本包含4个时间步,每个时间步包含2个特征。
数据集的形式应该如下:
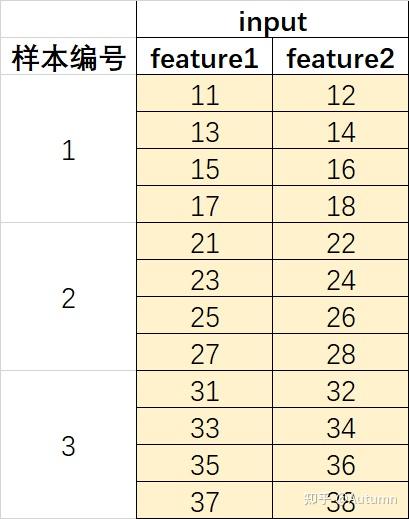
2.2 one和many的含义
当
b>1
时,即一个样本包含多个时间步时,就称这个序列为many;当
b=1
时,序列就是one。
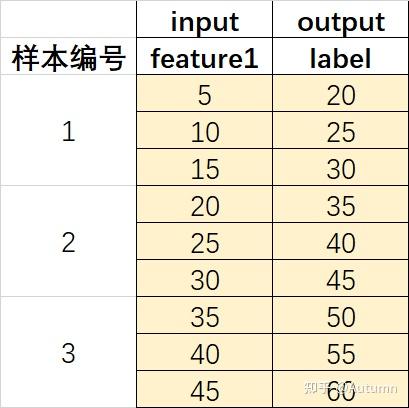
many to one表示多对一,即输入的序列是many,输出的序列是one,例如:
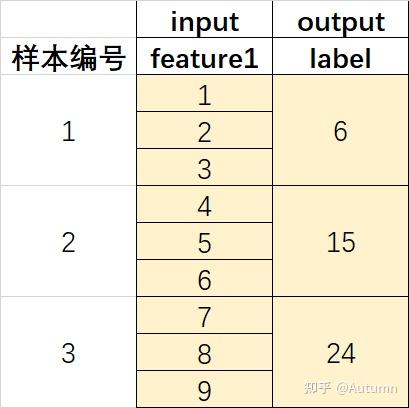
不要误以为下面这个也是many to one,实际上它是one to one。one to one包括只有1个特征的情况和多个特征的情况,下面这个就是多特征时。
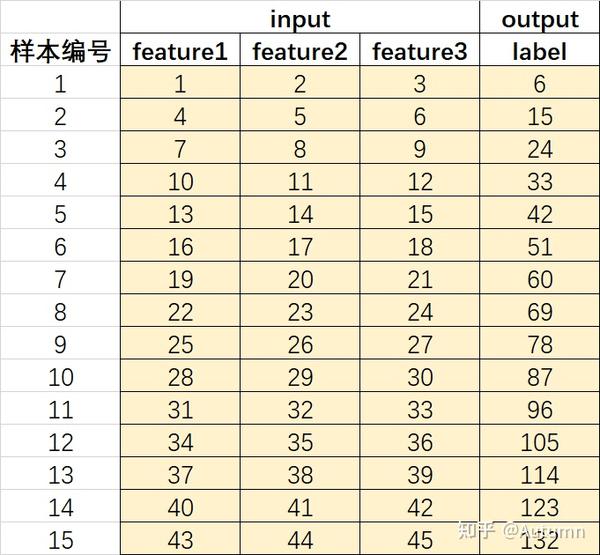
那么many to many应该是:
3 小结
综合第1节和第2节的方法,如果我们想要实现一次性多步预测,有3种形式:
1、 采用one to many的结构,一次输出多个时间步;
2、 采用many to many的结构,一次输出多个时间步;
3、 采用MIMO策略,一个时间步包含多个标签。
前两个方法对比第3个的优势在于,一次输出多个时间步能考虑到时序之间的依赖性。而一次输出的多个标签是相互独立的,没有考虑标签的序列依赖的性质。
参考资料
[2] 夏明朗(翻译):基于NN5预测竞赛的多步时间序列预测策略的综述和比较
[4] ChaoFeiLi:keras中使用LSTM实现一对多和多对多
[5] 奶油松果:张量维度的理解
[6] Usman Malik :Solving Sequence Problems with LSTM in Keras
