哈哈，我就知道是一个很低质的问题，所以大家都没有来回答，不过也没关系，进过这几天的资料查询，我还是找到了解决的办法。

方法其实特别简单，就是使用python的图网络工具箱networkx库。有时候不得不感叹，python真的是一门前人栽树，后人乘凉的好东西呀...好了废话就说到这里，让我们来实战看看到底怎么操作。

说在前面：这里使用的数据集是movielens的1M数据集中的ratings.dat文件，包含了3000多名用户对6000多部电影的接近100000条评分。这个数据集一共有四列，第一列是用户ID（1-3000+，整型），第二列是电影ID（1-6000+，整型），第三列是每一行中用户ID对应的用户对电影ID对应的电影的打分（1-5分，整型），第四列我就不介绍了，因为没啥用，我也不会用到，所以感兴趣的同学可以去movielens的官网，里面有对数据集的完整介绍。每一行的不同数据用“::”隔开。

接下来就是经典导包环节，我们的python数据处理三大金刚

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

当然不能忘记本次的主角：图网络工具箱networkx

import networkx as nx

先写这么多，突然有点事，下次完整写出处理流程。

回来了回来了，xdm，久等了，这段时间导师要求搞专利和小论文，忙的不可开交，立马就更！

首先是用pandas读取rattings.dat

#读取评分数据，rattings_path就是你存放rattings.dat的文件目录
ratings_file_dir=rattings_path
#设置表头
rnames = ['user_id', 'movie_id', 'rating', 'timestamp']
ratings_Origin = pd.read_table(ratings_file_dir, sep='::', header=None, names=rnames)
#把数据中无关的列（最后一列）剔除
ratings=ratings_Origin[["user_id","movie_id","rating"]]

处理好了打印出来是这样：

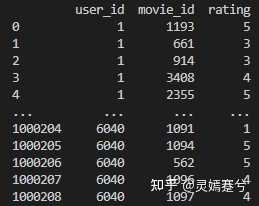
接下来就是把user_id和movie_id作为图的节点传入networkx里面，但是需要注意的是，user_id和movie_id都是int型，并且彼此都有重复的部分，重复的节点输入图中，后来的节点会覆盖前面的节点，因此需要对两个id值进行唯一化处理。

我这里唯一化的方式很简单了，就是给movie_id全部+10000，因为user_id的范围在[1,6040]，movie_id的范围在[1,3952]，加上10000以后刚好满足要求。

#将电影ID+10000，防止其和用户ID重复
ratings_movieId=ratings["movie_id"]+10000
ratings_userId=ratings["user_id"]
#替换原来的列     
ratings["movie_id"]=ratings_movieId
ratings["user_id"]=ratings_userId

接下来的任务就很简单啦，创建无向图，然后把节点和权值（权值就是评分值）输入图里面，图就构建好了。

#创建无向图
G = nx.Graph()
#添加节点，并按节点分组（0小组和1小组）
G.add_nodes_from(ratings["user_id"],bipartite=0)
G.add_nodes_from(ratings["movie_id"],bipartite=1)
#将ratings的每一行转换成一个三元组，并组合成list
edge_weight_list=ratings.apply(lambda x: tuple(x), axis=1).values.tolist()
#给图G中加入带权边
G.add_weighted_edges_from(edge_weight_list)

上面的代码bipartite参数是二部图的参数，表示给节点分组，目前还没发现这个参数有啥用，等后面继续学习。

最后，将图转换为邻接矩阵，即可进行后面的操作

#将图转换为邻接矩阵
A=np.array(nx.adjacency_matrix(G).todense())

打印出来看看

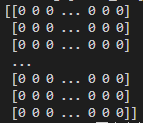
嗯....目光所及全是0，这是必然的，因为1M（100万）的数据对于(6040+3952)²的矩阵来说还是太稀疏了（实际上这个矩阵的维度是(6040+3706)²，因为有些电影没得人评分），下面给大家看看这个矩阵的数据大致示意图：

绿色的部分就是评分矩阵了，只不过方向不一样，黄色和蓝色部分是用户和电影各自的矩阵，因为用户和电影各自之间没有数据，就是一个全0的状态，只有两个绿色的矩阵中包含一些稀疏的评分数据，所以这个矩阵的稀疏度非常高。

到现在，矩阵的处理就基本完成了。

如果需要将这个邻接矩阵输入图神经网络里面训练的话，还需要做如下操作：

import torch
import scipy.sparse as sp
#，这里书接上文，将图转换为邻接矩阵
#A=np.array(nx.adjacency_matrix(G).todense())
#将邻接矩阵转换为稀疏矩阵的稠密表示形式
A_coo = sp.coo_matrix(A)
#取边的权值
weight = A_coo.data
indices = np.vstack((A_coo.row,A_coo.col))
#将边关系与权值转化为pytorch可处理的Tensor格式