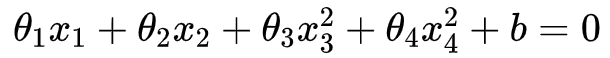显然，该分类问题具有非线性的决策边界。如果不增加特征，采用线性核的 SVM（以下简称线性 SVM）和逻辑回归都无法拟合，因为它们只能得到形如  的线性边界。
一个可行的办法是增加高次方项作为特征输入，比如以

作为线性 SVM 或逻辑回归输入，可以拟合形如

的决策边界（实际上它可以拟合圆或椭圆），对于图 1 所示的例子这可能是不错的模型。

然而，在实际案例中我们通常都无法猜到决策边界的“形状”，一是因为样本的特征数量很大导致无法可视化，二是其可能的特征组合很多。

对于上述非线性模型拟合的问题，我们之前介绍了采用核函数的 SVM，本文将介绍更通用的方法——神经网络。

考虑以下矩阵运算：

可以看到  的每个元素都是  的线性变换。一般地，对于权重矩阵 、输入向量 、偏置向量 ，可以得到 x 的线性变换 。

这里我们用   表示 k 行 n 列的矩阵， 表示 n 维向量。由于一些传统的原因，当我们说 n 维向量，一般指 n 维列向量，即 n 行 1 列的矩阵。

我们可以对 x 作多次线性变换得到最终的输出 y，如：

其中，我们用上标来区分不同变换的参数。
用图形表示为（假设向量  的维数分别是 2,3,2,1）。

上述连续变换我们称之为 3 层神经网络模型，它有 2 个隐藏层（hidden layer）、1 个输出层（output layer），并且输入 x 有两个特征，注意输入层不计入层数。一般地，如果输入 x 经过 L 次连续变换得到输出 y，那么该变换对应的神经网络模型有 L 层，并且具有 L-1 个隐藏层。
如图 1，隐藏层 1 有 3 个神经元（注意不包括偏置项），其中 ， 可以视为关于 x 的函数，我们也称之为神经元（neuron）或单元（unit），它接收上一层发出的信号 x，进行运算后将结果信号传递到下一层与其连接的神经元。如果某一层的任意神经元都分别连接到上一层的所有神经元，则该层称为全连接层（full connected layer，FC）。

作为个人的建议，你可以把一个层理解为一次变换（或映射），其输出将作为下一层（如果有的话）的输入。事实上，关于层的定义，我不认为我完全清楚，但是我通常会用矩阵运算或函数来看待神经网络的问题，所以如果你理解了原理，这些名词其实不重要。
关于神经网络的同义名词。由于部分人不喜欢神经网络与人脑机制的类比，所以他们更倾向于将神经元称为单元，此外，神经网络也被称为多层感知机（multilayer perceptron）。说实话我也不喜欢，但是为了尽可能减少信息差，本文将采用使用率更高的名词。

现在，我们来分析如何用神经网络模型解决本文开篇的非线性分类问题。
仔细分析可以发现，x 经过多次线性变换的结果仍然是关于 x 的线性变换，显然，为了拟合非线性的模型我们需要加一些“非线性的运算”。具体的操作如下：

其中， 𝑓(·) 是对矩阵或向量的点操作（elementwise），即：

𝑓 称为激活函数（activation function），activation 一词来源于神经科学，稍后我们将进一步探讨。考虑以下激活函数：

对于只有一个隐藏层的神经网络模型，以 Sigmoid 函数为激活函数，即：
假设隐藏层有 N 个神经元且输出 y 为实数，则 y 可以表示为如下形式：

可以证明 𝐺(𝑥) 是一个通用近似器（universal approximator），能够近似任何函数。
某种意义上，可以认为神经网络自动进行了特征组合，我们需要做的是找到合适的模型架构，并且通过优化算法得到拟合数据样本的模型参数。

对于本文开篇的分类问题，我们只需要一个两层的神经网络模型，即有一个隐藏层和一个输出层，隐藏层单元数量一般可以取输入特征维数 n 的倍数，比如 2n。模型可以用矩阵运算表示：

你可以检验上述运算是否符合矩阵乘法规则。

关于隐藏层单元数量。通常隐藏层单元数量越多越好，一个直觉的理解是，如果我们把待拟合的目标函数看成一个具有无穷项及任意系数的多项式函数，更多的隐藏层单元意味着更多的独立参数，它将有更强的拟合能力，但是需要更大的计算量，当然拟合能力强也意味着更容易过拟合，因此我们还会在误差函数中加入正则化项，后续文章将深入探讨。

此外，隐藏层单元数量一般不能小于输入特征维数，特别是对于当你的模型使用了 ReLU 这样的激活函数时，它将有可能无法拟合目标函数。

注意到我们用 Sigmoid 函数将模型输出 y 映射到（0,1）区间，但这里的 Sigmoid 通常不认为是激活函数，仅仅作为分类问题的归一化作用。 表示第 i 个训练样本，M(x) 表示模型的输出，则其误差函数（用小写 θ 表示所有模型参数）。

接下来我们可以用梯度下降（将在下一篇文章探讨）得到最小化误差的模型参数 ，于是，对于给定的测试样本 ，我们给出的预测是：

对于非线性的回归问题，我们模型可以是：

此时误差函数应该用最小平方误差（mean squared error）：

总结一下，神经网络算法的基本步骤：
1) 设计模型架构（提出假设）
2) 设定误差函数
3) 最小化误差（求极值点）

关于模型架构。虽然具有一个隐藏层的神经网络已经可以模拟大部分函数，但是实践证明深度神经网络（即有更多的隐藏层）在图像识别和自然语言处理等任务中具有更优的表现，因此有各类复杂的模型被设计出来，并在相应任务中取得了很好的效果。

一些典型的模型架构，如 CNN（常用于图像类任务），RNN（常用于序列类任务），Autoencoders（常用于特征学习），GAN（常用于生成类任务）。

关于最小化误差。在实际任务中，误差函数通常无法得到解析解，因此我们一般采用梯度下降这样的迭代算法以期得到近似值，但这里面需要考虑各类“函数形状”所带来的问题，我们将在后续文章介绍这些问题及其解决方案。

▲ 图3.1 Sigmoid

▲ 图3.2 Tanh

Sigmoid 函数。最古老的激活函数，表达式 ，据说选中它的原因是其函数特征很像生物学中的“全或无定律”（all or none law）——神经元对于超过阈值的刺激强度以最大的脉冲振幅作出反应，而对于低于阈值的刺激不作反应。
如图 3.1，Sigmoid 函数在x很大时趋近于 1 而在 x 很小时趋近于 0， 然而，Sigmoid 函数的梯度也在两端快速趋近于零，这将有可能导致梯度消失（这是后向传播算法和计算机精度带来的问题，我们将在后续文章探讨），进一步导致参数无法更新（可以说模型停止了“学习”）。

Tanh 函数。Tanh 与 Sigmoid 有类似的特征，可以由 Sigmoid 缩放平移得到，即 𝑇𝑎𝑛ℎ(𝑥)=2∗𝑆𝑖𝑔𝑚𝑜𝑖𝑑(𝑥)–1 。它的优点是值域为（-1,1）并且关于零点对称，对于零均值的输入将得到零均值的输出，这将有利于更高效的训练（类似于 batch normalization 的作用）。需要注意的是，Tanh 仍然有梯度消失的问题。

ReLU 函数。表达式为 𝑅𝑒𝐿𝑈(𝑥)=𝑚𝑎𝑥(0,𝑥) ，一般来说，它相比 Sigmoid 和 Tanh 可以加速收敛，这可能得益于其在正半轴有恒为 1 的梯度，另外由于只需要一次比较运算，ReLU 需要更小的计算量。注意到 ReLU 在负半轴恒为零，这将导致神经元在训练时“永久死亡”（即对于上一层的任何输入，其输出为 0），从而降低模型的拟合能力，事实上，这也是梯度消失的一种表现。

关于 ReLU 的“死亡”。考虑以 ReLU 为激活函数的神经网络模型（通常同一个模型只用一种激活函数），以任意神经元为例，将其视为函数 θ，其中 x 为上一层的输出向量。假设某一次梯度更新后  θ，进一步假设任意  为数值很大的负值，考虑到上一层的输出 x≥0，容易发现对于后续的输入，f(x) 取值将有可能一直为 0。上述分析思路同样适合 Sigmoid 函数，当然这也进一步解释了 Tanh 零均值输出的优势。如果你对于 batch normalization 有所了解，应该可以发现它将有助于改善“Dying ReLU”问题。

类 ReLU 函数。实践证明 ReLU 在多数任务中具有更优的表现，特别是在深度神经网络中。考虑到 ReLU 本身的缺陷，有许多改进版的 ReLU 被设计出来并得到了不错的效果。主要改进的地方有两点，一是 ReLU 在零点不可导，二是其在负半轴取值为零。其中比较典型的有：

Leaky ReLU:

GELU:

Swish:

▲ 图4.1 ReLU

▲ 图4.2 Leaky ReLU

▲ 图4.3 GELU

▲ 图4.4 Swish

Leaky ReLU 给 ReLU 的负半轴增加了一个微小的梯度，改善了“Dying ReLU”的问题。GELU 用了高斯累计分布来构造 ReLU，著名的 NLP 模型 BERT 用的是 GELU，参考 [1]。Swish 是通过自动化技术搜索得到的激活函数，作者做了大量的对比实验表明 Swish 在不同的任务中均有超出其他类 ReLU 函数的表现（包括 GELU），参考 [2]。

Swish 和 GELU都属于“光滑 ReLU”（smooth ReLU），因为处处连续可导，一篇最近的论文展现了用光滑 ReLU 进行“对抗训练”（adversarial training）的良好表现，参考 [3]。

关于激活函数的选择。没有人任何科学家会 100% 确定地告诉你哪个函数更好用，但是如果按照实验结果，我们可以说类 ReLU 函数目前在多数任务中有更优的表现，就个人的建议，Swish 和 GELU 会是不错的选择，Swish 的论文虽然以实验表明其优于 GELU，但 Google 在 BERT 中使用了 GELU。其他激活函数，可参考 [4]。

上文我们提到了通用近似器的概念，事实上这就是神经网络之所以有效的原因，而其关键的部分则是激活函数。

在“通用近似理论”（universal approximation theorem）领域，可以分为两类近似理论，一类研究任意宽度（arbitrary width）和有界深度（bounded depth）的情况，另一类是任意深度和有界宽度。

比如上文的 G(x) 属于任意宽度和有界深度，即 depth >= 1，width 根据近似的目标函数可以任意调整。在深度学习领域，有很多关于神经网络隐藏层的宽度（width，平均单层神经元数量）和深度（depth，模型层数）如何影响神经网络模型性能的研究，比如，是单层具有 1000 个神经元的隐藏层，还是 10 层具有 100 个神经元的隐藏层表现更好。

值得注意的是，对于某些激活函数，宽度如果小于等于某个数值（对于 ReLU，这个数值是输入特征维数 n），无论其模型深度多大，都存在一些其无法模拟的函数。详情请参考 [5]，以及关于深度神经网络的研究 [6]。

以下一个简单的例子展示了以 ReLU 为激活函数的单隐藏层神经网络模型，其拟合效果与隐藏层单元数量的关系，为了方便可视化，拟合的目标是一元二次函数（x>0）。图 3.1 为随机采样的 50 个样本，图 3.2、3.3、3.4 分别为隐藏层单元数量取 1、2、5 时的拟合曲线。

▲ 图5.1

▲ 图5.2

▲ 图5.3

▲ 图5.4

可以看到随着隐藏层神经元数量的增多，模型的拟合能力逐步增大，如果神经元数量太小，则有可能无法在允许的误差范围内拟合目标函数。

一个有趣的事情是，当我们不用激活函数时，相当于我们用了一个恒等函数 f(x)=x  作为激活函数，这将导致我们的模型只能拟合线性函数。但是，ReLU 仅仅简单地“舍去”负值就取得了通用近似器的效果，有点类似于二极管对交流电的整流作用，这也是 ReLU 名称的由来（Rectified Linear Unit）。

事实上，计算机的运算就是基于开关控制的逻辑电路，所以从这个角度，ReLU 似乎有一种二进制的美感。

[1] Gaussian Error Linear Units (GELUs). Dan Hendrycks. University of California, Berkeley. 2016.
[2] Searching for Activation Functions. Prajit Ramachandran. Google Brain. 2017.
[3] Smooth Adversarial Training. Cihang Xie. Google. 2020.
[4] Activation function. Wikipedia.
[5] Universal approximation theorem. Wikipedia.
[6] Learning Functions: When Is Deep Better Than Shallow. Hrushikesh Mhaskar. California Institute of Technology. 2016

原文：https://mp.weixin.qq.com/s/8Sg9VBVTbN2bJyntQPQTyg