DropKey for Vision Transformer

--------------------------------------------------------------------------------------------
Dropout:当模型比较复杂,而训练样本却较少的时候,容易发生过拟合。通过在前向传播的过程中,让某个神经元的激活值以一定的概率 P 停止工作,不过度依赖于某些神经元,模型变得更鲁棒,可以有效避免模型发生过拟合。
------------------------------------------ - -------------------------------------------------
摘要 :作者对三个核心问题进行了研究。 第一 ,在注意力层应该对 什么 信息执行 Dropout 操作? 第二 ,如何设置 Dropout 概率 ? 第三 ,是否需要像 CNN 一样的 结构化 Dropout?
第一 ,该方法在计算注意力矩阵之前执行 Dropout 操作,并将 Key 作为 Dropout 单元 ,得出一种新的 dropout pre softmax方法,有助于缓解特定模式的过拟合问题,并增强模型全局捕获重要信息的能力。 第二 ,作者提出了一个 递减 Dropout 概率的计算方法,即随着自注意力层的加深而减小 Dropout 概率。 第三 ,作者最后尝试基于 patch 的 Dropout 操作,发现其对于 ViT 来说并不是必需的。
Introduction
ViT 被广泛地应用于计算机视觉任务中,通过将图片分割为固定数量的图像 patch,并引入了多头自注意力机制来提取包含相互关系的特征信息。自注意力的 Dropout 技术对于实现良好的泛化性起着至关重要的作用,却被目前的研究所 忽视 。
该论文提出了一种即插即用、仅需要两行代码便可实现的 DropKey 用以缓解 ViT 类方法的过拟合问题。不同于已有的针对神经元的 Dropout, DropKey 将 Key 设置为 drop 对象,并验证了其可以对高注意力值部分进行惩罚,同时 促进 模型更加关注与目标有关的其他 patch,有助于捕捉更鲁棒的全局特征。

Method
DropKe y的主要思想是 自适应 地调整注意力权重以获得更 平滑 的注意力向量。
(1) Methodology
基于 VIT 的模型倾向于依赖于 patch 局部特征,而不是全局信息。 为了缓解这个问题,作者认为可以通过使模型为每个 patch 学习更 平滑的注意力权重 来减少局部偏差。 为此作者尝试 减少 具有 高注意力权重 补丁的注意力权重,反之亦然。 在这项工作中 DropKey 通过规范化执行 Dropout 操作隐式地实现了上述目标。
具体来说,通过给定的图像 I \in R^{C \times H\times W} ,首先将其切成 n_h \times n_w 个patch. 然后 x 用作自注意层的输入, 输出 o 可以按下式计算

其中 q_i, k_j, v_j 表示补丁 i^{th} 的 query,补丁 j^{th} 的 key,补丁 j^{th} 的value, d_j 为 drop 率, scale = \sqrt{n_c} 为缩放率。为了降低复杂度,作者专注于一个 Head 。 通过执行 DropKey, 能够 自适应 地调整注意力权重以使其更平滑。
通过在训练阶段引入 DropKey,得到了模型的 期望 输出为:

其中作者称 {\color{red}{c_j}} 为和 d_j 、p_j 相关的平滑系数。
当 p_s > p_t , 1\leq s、t \leq n_h n_w 时,有

可以发现 c 作为一个参数,隐式地促进模型减少对具有大注意力权重的补丁 p 的倾向,并以较小的注意力权重提高 patch 的有效性。 同时 p 可根据训练阶段样本的分布进行自适应调整,无需任何人工设计。 由于作者在推理阶段删除了 DropKey,训练和推理阶段的输出期望不一致,这会 降低 性能。
{\mathbb{\color{green}{梯度优化的角度进行分析:}}}
首先考虑一个简单但通用的优化目标,如下所示:

其中 p_j \in R,v_j \in R^r 表示可学习的参数, y 表示目标,文中 p_j ,v_j 为注意力权重和系数。二维空间中 v_j 可以分解为 v_j=\beta_je+\alpha_j ,其中 \beta 为系数, e 为单位向量, \alpha_j 为垂直于 y 的标量。
方程 5 的拉格朗日函数如下:

为了更好地分析梯度,对 p_j,v_j 求偏导:

为了简化计算流程,令:

根据链式法则,得到:

根据上式可以得出,当 p_s >p_t 时, \frac{\partial L}{\partial \beta_s} <\frac{\partial L}{\partial \beta_t} ,在后向传播中会导致 \frac{\partial L}{\partial p_s} <\frac{\partial L}{\partial p_t} 。通过 \frac{\partial L}{\partial p_s} 减去 \frac{\partial L}{\partial p_t} ,得到下式:

由于所有参数都是随机初始化的,因此可以假设初始解与最优解具有较大的差距,所以 \left| \beta_j^{(0)} \right| \ll M ,即方程后半部分在 方程 1 1 中起着主导作用。因为 \frac{\partial L}{\partial \beta_s} <\frac{\partial L}{\partial \beta_t} ,所以 \beta_s 比 \beta_t 更新速度快,导致 \beta_s>\beta_t ,于是 \frac{\partial L}{\partial p_s} <\frac{\partial L}{\partial p_t} 。基于以上分析,可以得出结论,一个更大的 p 会促进 \beta 更大,而更大 \beta 将进一步促进 p 增加。于是 DropKey 通过引入参数 c 可以有效地避免局部偏差的影响以强制 p 平滑。
(2) Implementation
\color{green}{What-to -drop?}
在每次训练中,DropKey 都会随机屏蔽输入键映射的一定速率的键。 值得注意的是,我们为每个查询生成屏蔽键映射,而不是为所有查询向量共享相同的屏蔽键映射。具体来说,给定查询 Q\in R^{n_hn_w \times n_c} , 键 K\in R^{n_hn_w \times n_c} 和值 V\in R^{n_hn_w \times n_c} ,首先计算 Q 和每个 K 的点积,并除以比例因子 \sqrt{n_c} 。然后随机生成一个掩码矩阵 D\in R^{1\times (n_hn_w \cdot n_hn_w)} ,强制相似性矩阵的某些元素为 -INF。

最后,通过给定的掩码相似性矩阵作为输入来计算注意力权重矩阵。patch 最终的输出计算为:

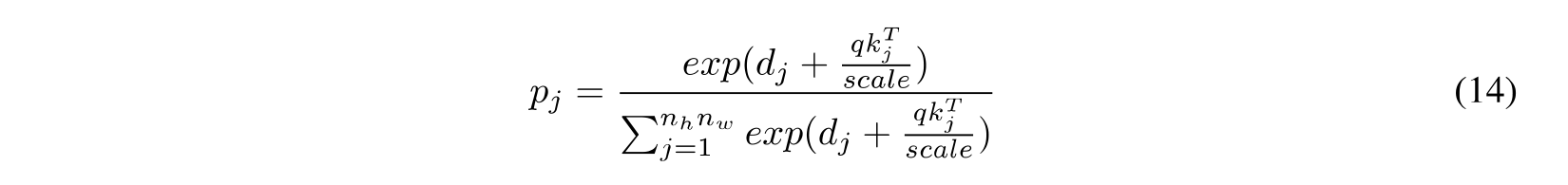
其中 q_i, k_j, v_j 表示补丁 i^{th} 的 query,补丁 j^{th} 的 key,补丁 j^{th} 的value, d_j 为 drop 率, scale = \sqrt{n_c} 为缩放率。等式 13 和等式 14 是等式 1 和等式 2 的等价形式。

\color{green}{Scheduled-Drop-Ratio}
浅层 注意力层专注于 低级 视觉特征,而 深层 注意力层旨在对 复杂 的信息进行建模。 因此,作者尝试为更深的层设置较小的 Drop 比率,以避免丢失重要的相关信息。 具体来说,在 Dropout 中, 不是以固定 的概率随机丢弃,而是在训练阶段 逐渐减少 各层上丢弃的 K 的数量。 作者指出这种计划的丢弃比率不仅适用于 DropKey,而且还显著提高了 Dropout 的性能。
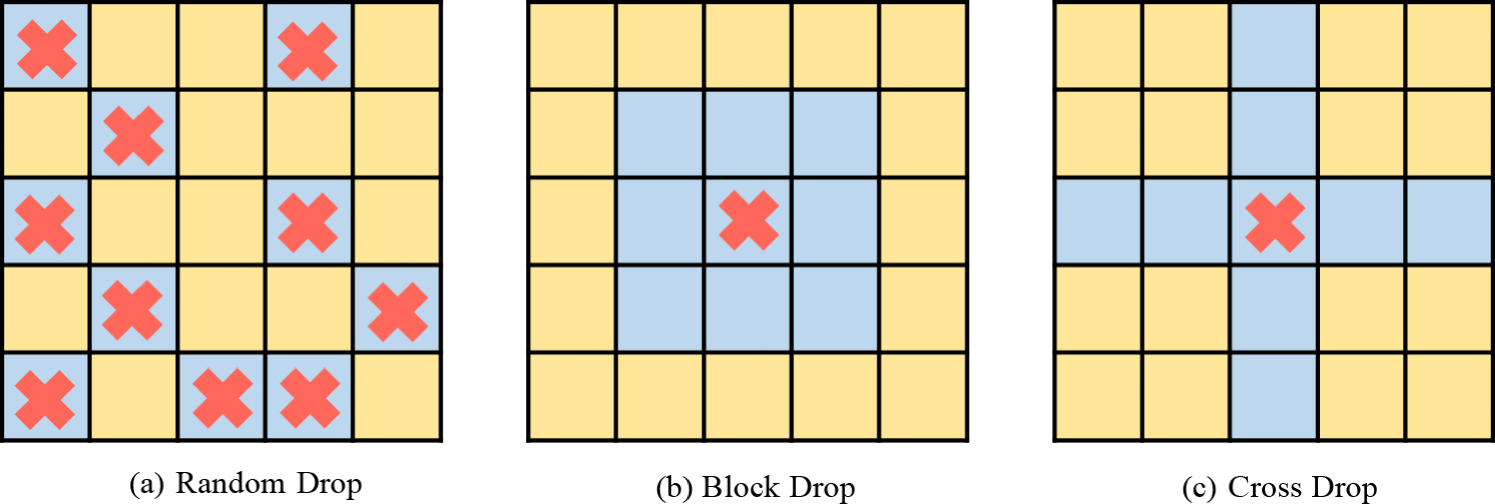
黄色补丁用作 KEY与 QUARY 交互的应答键,蓝色补丁被丢弃。红色符号表示有效种子,DropKey-Block 和 DropKey-Cross 的窗口大小分别为3和1。
Algorithm 1 Attention with DropKey code
1 # N: token number, D: token dim
2 # Q: query (N, D), K: key (N, D), V: value (N, D)
3 # use_DropKey: whether use DropKey
4 # mask_ratio: ratio to mask
6 def Attention(Q, K, V, use_DropKey, mask_ratio)
7 attn = (Q * (Q.shape[1] ** -0.5)) @ K.transpose(-2, -1)
9 # use DropKey as regularizer
10 if use_DropKey == True:
