CS224W 3. Node Embeddings
3. Node Embeddings
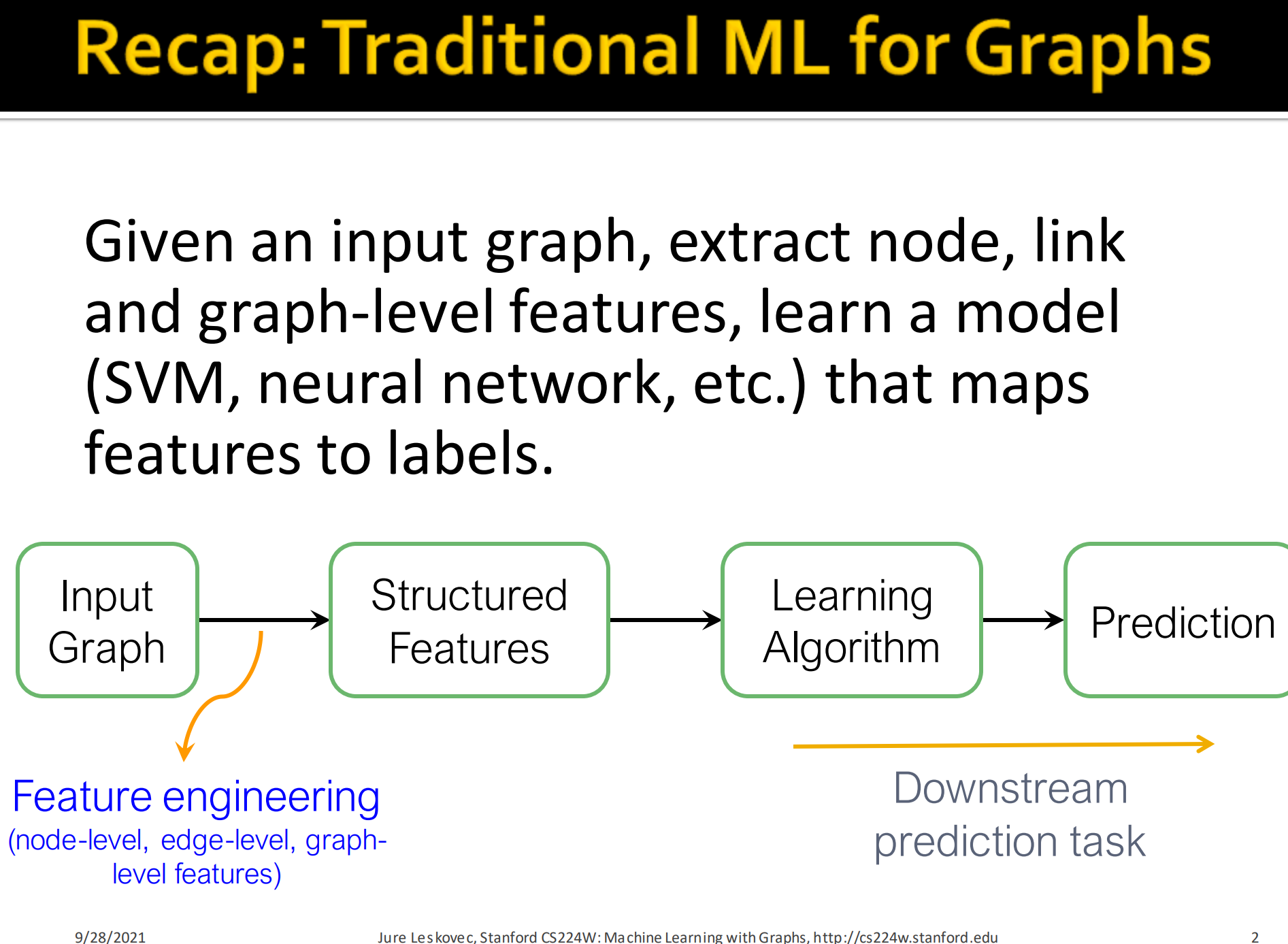
1. Recap: Traditioal ML for Graphs
传统的图机器学习 :
1. Graph representation learning
图的表征学习 :
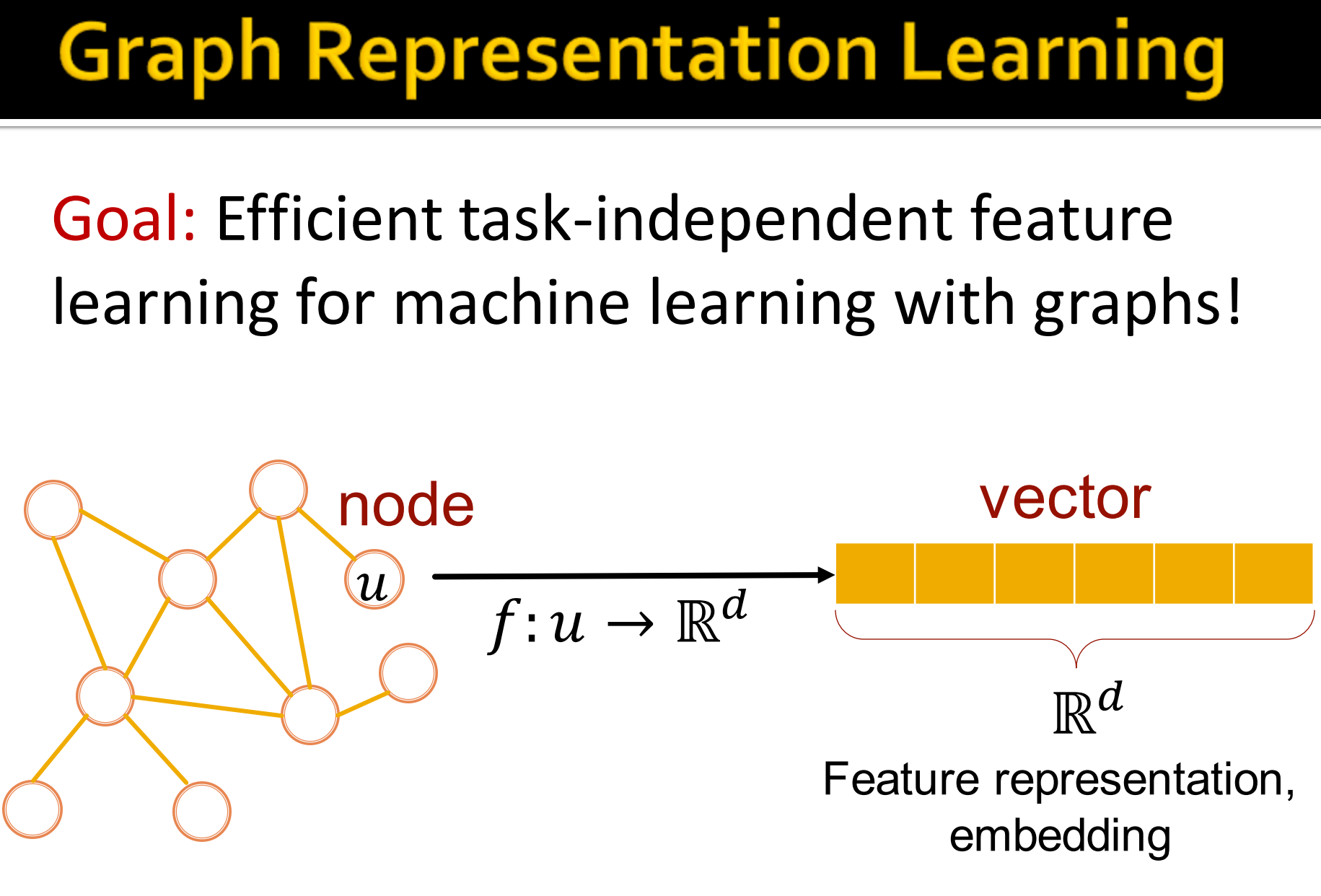
目标:图机器学习的高效的 任务无关特征 学习。对于图,要抽取到任务无关的的特征,这样下游任务不同,也能用。
如上图,就是把节点u,拿函数 , 映射成向量v, . 这就是 特征表示 或者更具体地说 embedding .
2. Why Embedding?
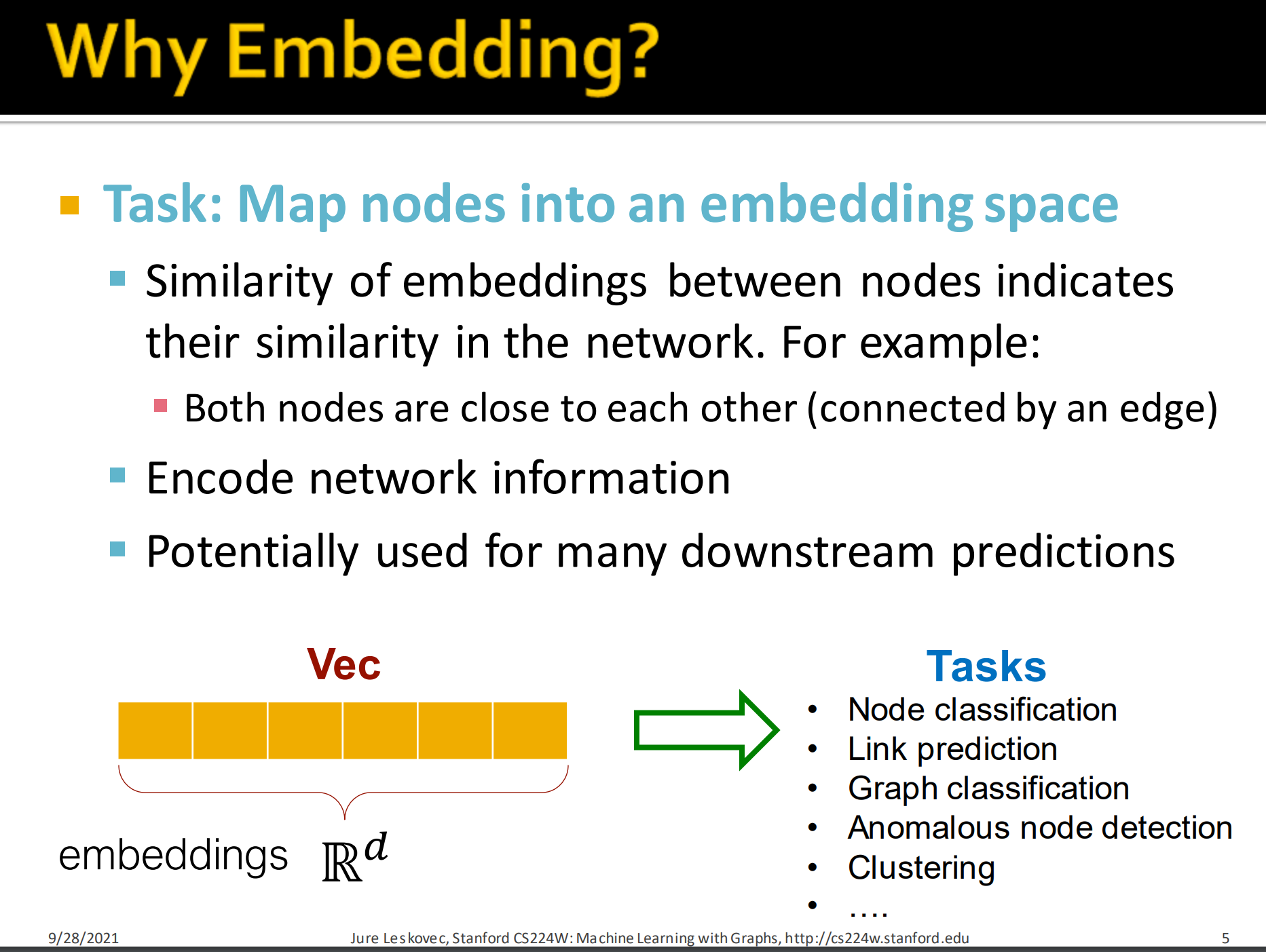
- 节点间embeddings的相似性表示它们在网络中的相似性。如节点彼此接近(被同一条边连接),其embedding相似度要高。
- 编码网络信息
- 有潜力为许多下游任务做预测
-
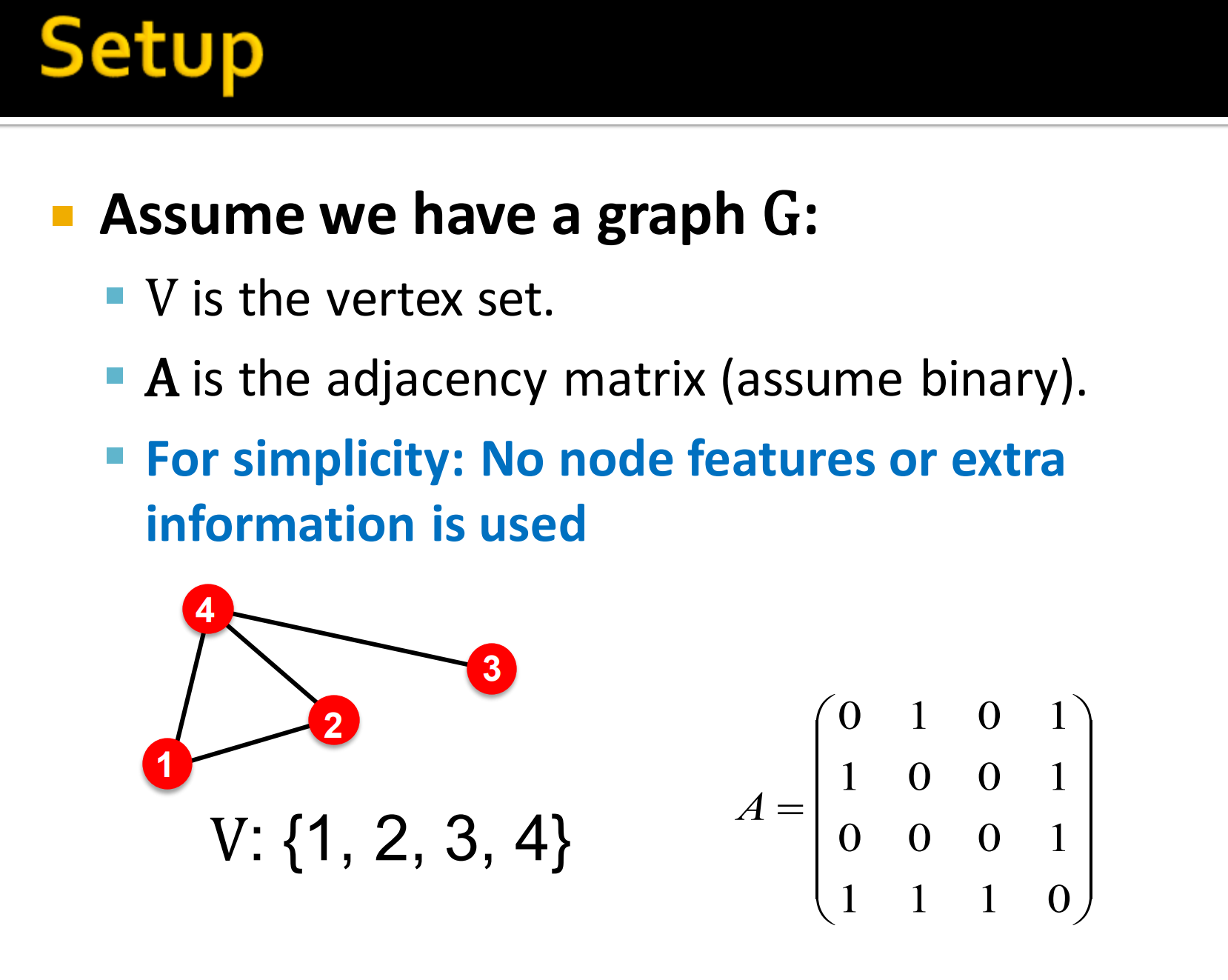
假定有一个图G:
- 是邻接矩阵(假定是二值化的)
- 为了简单起见,不使用节点特征和额外的信息
- Encoder 将节点映射到embeddings
- 定义节点相似度函数(就是一个衡量原始网络中节点相似度的函数,如余弦相似度)
- Decoder 记为DEC将embeddings映射为相似度分数
- 优化encoder参数使得式1成立。
- Encoder : 映射每个节点到低维度向量。
- 相似度函数: 明确编码后向量空间和原始网络是怎样的映射关系,如上图,就是原始网络中u和v的相似度和这两个节点embedding后的点积是对应的。
- 浅层的编码器: embedding lookup
- 参数优化: 包含 即图中所有节点embedding .
- 深层的编码器GNNs将会在Lecture 6讲到。
- Decoder:基于节点相似度
- 目标:最大化相似节点对(u, v)的 .
- 上述方法的关键点是怎么定义 节点相似度 ?
-
两个节点应该有相似的embedding如果它们…
- 有共同邻居节点
- 有相似的结构特征
- 接下来将用 随机游走 来学习获得节点相似度,和怎样为该相似度指标优化embedding。
-
监督学习和非监督学习方法都可以用来学习节点的embedding
- 不利用 节点标签
- 不利用 节点特征
- 目标是直接估计一组节点坐标(embedding),以便保留网络某些结构
-
embeddings都是任务无关的
- 不为特定任务训练但可以在任何任务上使用
- 向量 : 节点u的embedding (我们要学习到的)
- 概率 : 基于 的预测概率,即从节点u开始随机游走到节点v的概率
- Softmax函数 :将K实数向量转化为总和为1的K概率值,Softmax函数分子就是将原值 转化为e的幂次,分母表示归一化因子来确保和为1
- Sigmoid函数 :S-shape函数将实数值转化为(0, 1)之间的值
- 估算使用策略R的随机游走从节点u访问到节点v的概率
- 这个概率就是节点u和v的相似度,我们可以根据这个概率来优化embedding,在embedding空间的相似度,这里 ,就是编码的随机游走相似度。
-
可解释性
:灵活的随机的节点相似度定义,随机游走每步的游走表示了节点的局部信息,游走路径序列表示了全局信息,这样包含了局部和高阶的邻域信息。
- 想法 :如果以较高的概率随机从节点u访问节点v,那么u和v是相似的(高阶,多跳的信息)。
- 高效性:不需要在训练时考虑所有节点对;仅仅只要考虑随机游走时的共现对,节省了计算量
- 直觉 : 找到节点在保留相似度的d维空间的embedding。
- 想法 :学习节点的embedding使得网络中邻近的节点的embedding是相近的,就是如果在网络中邻近的节点,embedding后相似度要高,这样就将图结构的网络空间信息embedding到embedding space。
-
给定节点u,怎么定义邻近节点?
- 表示某一随机游走策略R中获得的节点u的邻居节点。
- 目标是学习一个映射
- 对数似然目标函数:
- 给定节点u,我们希望学习特征表示是对出现节点u随机游走邻域节点 的预测。
- 使用固定长度的游走策略R从图中每个节点u进行随机游走
- 对每个节点u记录其 ,就是从u出发随机游走得到的节点集合(这是个multiset,因为有重复元素,随机游走会重复访问多次)
- 按照给定节点u预测其邻域节点
- 直觉 : 优化embeddings 来最大随机游走共现的似然概率。
- 对 使用softmax有:
- 第一个求和是对图中所有节点u,要整体最大不能是单一节点
- 第二个求和是对从u到v的所有随机游走中出现的节点v求和
- 最后黄色部分是预测在随机游走中u和v共现的概率
- 以节点度对应的概率来采样k个负样本节点
-
两个决定k的因素
- 更高的k对应更可靠的估计值
- 更高的k对应着更多的负样本带来的更高的偏差
- 获得目标函数后,我们怎么最小化它呢?
-
梯度下降来最小化损失函数 :
- 在所有节点u中随机选取一个初始化,得到
-
迭代直到收敛
- 对所有节点u,计算导数
- 对所有节点u,计算以学习率为 更新迭代后的导数:
- 从图中每一个节点进行短径固定长度的随机游走
- 对每一个节点u记录其邻域节点 , 这是一个从u开始随机游走得到节点的multiset,有重复节点
- 使用随机梯度下降算法来优化embedding,使得损失函数最小
-
前面已经讲了怎么在给定策略R的情况下优化embeddings
-
那么我们应该使用什么策略进行随机游走呢?最简单的想法:直接固定长度,每个节点都无偏的随机游走。
但问题是这样的策略使得相似度有非常大的局限性。
-
我们怎么将其泛化呢?
12. Node2Vec
- Overview of node2vec
- 目标: 在特征空间嵌入相似性来表示邻近节点
- 将这个目标表示为最大似然优化问题,对下游预测任务独立。
-
关键点:节点u的邻域节点 灵活性能丰富的节点embeddings
-
进一步的有偏的2阶(2阶就是走2步)随机游走R可以生成节点u的邻域节点 的邻近节点
- node2vec: Bias Walks
- BFS广度优先搜索 : 以某节点为起点搜索其所有的邻居节点,局部视角
- DFS 深度优先搜索 : 以某节点为起点直到搜索到终点为止,全局视角
-
两个超参数
- Return parameter p(返回参数) ,用来控制是否返回以前的节点。
- In-out parameter q(出入参数) , 表示在起点附近游走inwards(类似BFS)和向更远处游走outwards(类似DFS)的比例,直觉来说就是BFS和DFS的比率。
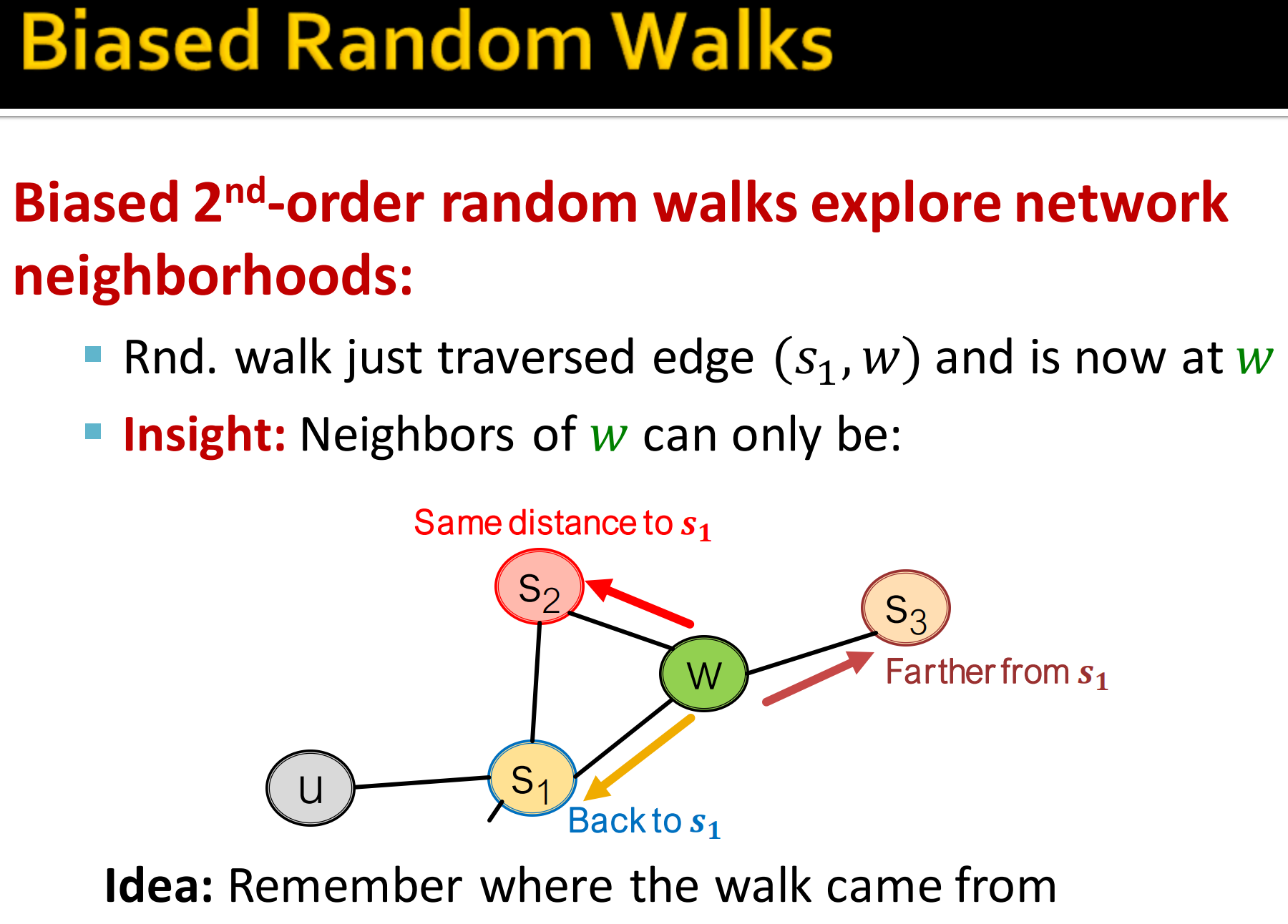
- 假设通过边 到达w节点
- 那么现在w节点的邻居节点可能是 。这跟最开始的起点 的意义是不一样的,具体如上图所示。
-
通过边 走到w节点,下一步去哪?
这里,如上图所示,走到下一个节点的的概率是不一样的。(注意, 不是归一化的概率,加起来和不为1)
-
p, q是 模型的转移概率。
如上图所示,前一步通过边 到达节点w。现在走到的节点w,邻居节点有 。具体怎么设计p, q概率呢?
根据上一跳节点和下一跳节点的距离设计,说到距离,就要明确这两点在哪?上一跳节点为 ,下一跳为 。
论文 node2vec: Scalable Feature Learning for Networks 3.2.2 Search bias α 部分提到:
这里 分别表示上一跳节点,和未来要走到的节点。 表示距离。
上图中, 到 的距离为0,所以为 。
还有可能跳到节点 到 的距离分别为1, 2, 2,就得到如图示的转移概率。这时的概率还没有归一化,最后要归一化。
- 类似BFS的游走:较小的p值,那么 就较大,会回到上一跳节点。
- 类似DFS的游走: 较小的q值,会往跟上一跳较远的距离跳
- 计算随机游走概率
- 从每个节点u开始模拟策略r距离为l的随机游走
- 用随机梯度下降优化node2vec 目标
- 核心想法: 嵌入节点使得 嵌入空间的距离 反映 原网络的节点相似度
-
不同的节点相似度表示
- 简单的: 如果两个节点相连就相似
- 邻居的重叠度(第二节谈到)
- 随机游走方法(本节内容)
- 记录所有的长度l的匿名游走
- 将图表示为这些匿名游走的分布
- 设定l=3
-
将图表示为5维的向量
- 因为长度为3的匿名游走有5种pattern
- 图中出现匿名游走pattern i的概率.
- 独立地采样m条 随机游走 路径来近似 匿名游走 pattern
- 用这些采样得到的随机游走路径的概率分布来表示图
- 就是将所有的匿名游走的embedding 加上图的embedding 一起输入学习,其中 。
- 想法 :跟node2vec类似,通过预测下一跳周围的walk来学习embed walks。
- 输出:也就是预测,输入图的embeding 。这个 也是要学习的目标。
- 从节点1开始,采样获得匿名随机游走,如上图所示 。
- 学习预测 walks 共现在 窗口内的概率,比如,当窗口为2时,给定 去预测
- 对数里面,表示给定 图 的embedding 和一定范围窗口内的 采样匿名随机游走 情况下,下一个walk出现的概率。
- 从节点u获取长度为l的T条不同的随机walks
- 学习预测将会出现在共现 窗口内的walks
- 评估匿名游走 的embedding 。
- 将所有匿名walk的embedding加起来再求平均,从 到 总共 个embeddings,就除以
- 然后将平均的embeddings和图的embedding 拼接起来
-
通过优化可以学习到图的embedding 表示
- 是不是简单地对walk embedding 求和? 是不是下一个 的残差?
- 论文中, 是一个独立优化的向量参数,跟 一样
-
用 来做预测,如图分类。
- 选择1: 内积和 (小节2中提到的)
- 选择2:把 输入到神经网络来对图分类
- Graph类似paragraph或document
- Anonymous walk类似于 word
- 方法一:简单粗暴直接embed node求和平均它们
- 方法2:创建super-node映射子图,然后embed 这个super-node
- 方法3: Anonymous Walk Embeddings
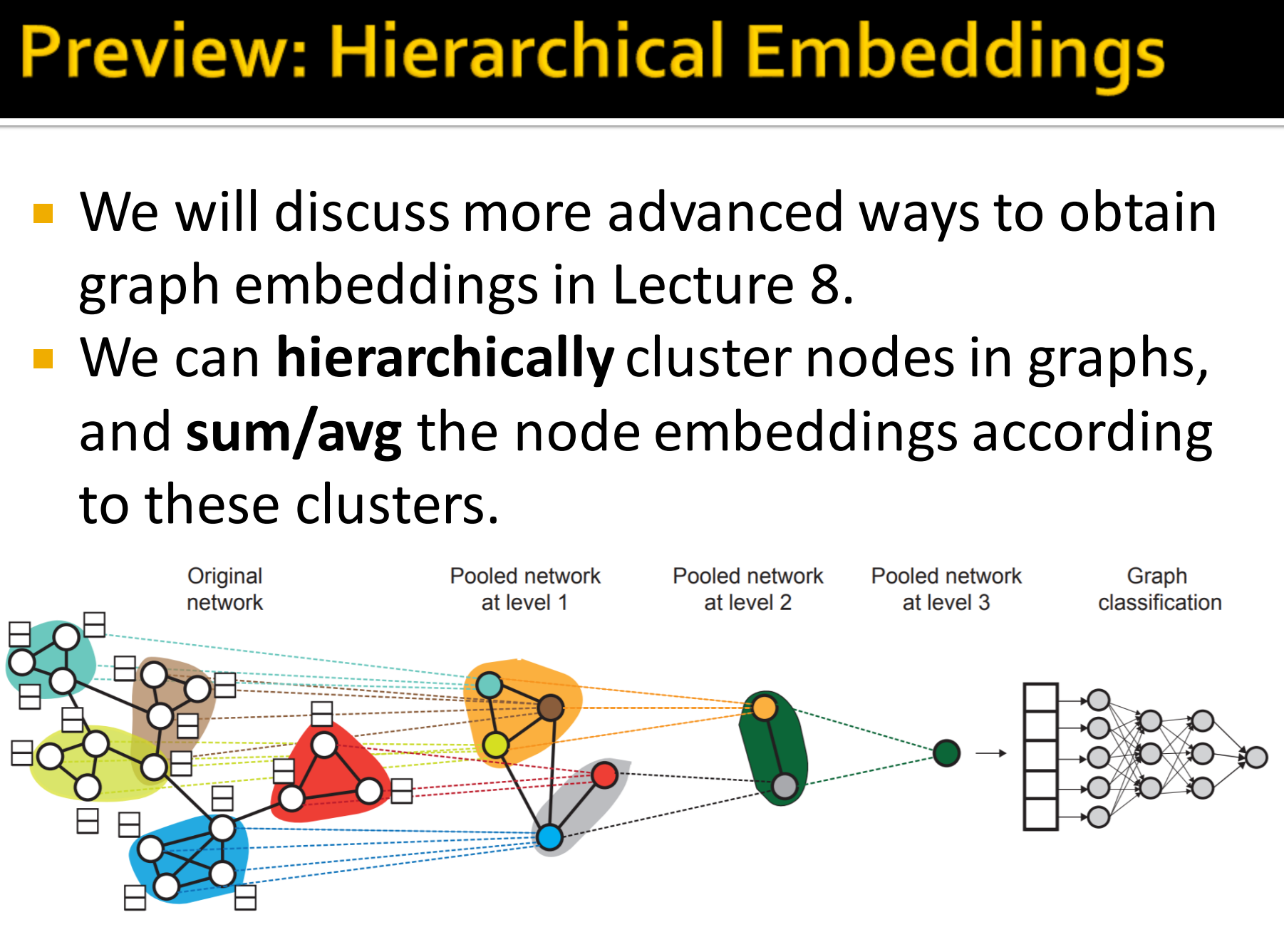
- Lecture 8 将学习更先进的方法来获取graph embeddings
- 在图中使用层次聚类节点,然后对这些聚类进行求和/平均得到节点embeddings
- 聚类/社区发现: 聚类 点
- 节点分类:基于 预测节点i的标签
- 边预测: 基于 预测边 , 可以通过平均,平均,哈达玛积(Hadamard), 求embeddings的差值
- 图预测:通过聚合节点embeddings或匿名随机游走获得的图embedding 来预测图的标签
接下来看看Anonymous Walk Embeddings 跟 doc2vec(来自 Distributed Representations of Sentences and Documents )类似之处。
比较两幅整体结构图,
更多展开分析就不进行了(如公式),只是说下很多研究都是借鉴前人或其它方向的思想。
8. Summary
3种graph embedding方法:
9. Preview:Hierarchical Embeddings
10. How to Use Embeddings?
怎么使用节点的embeddings :
6. Sampling Anonymous Walks
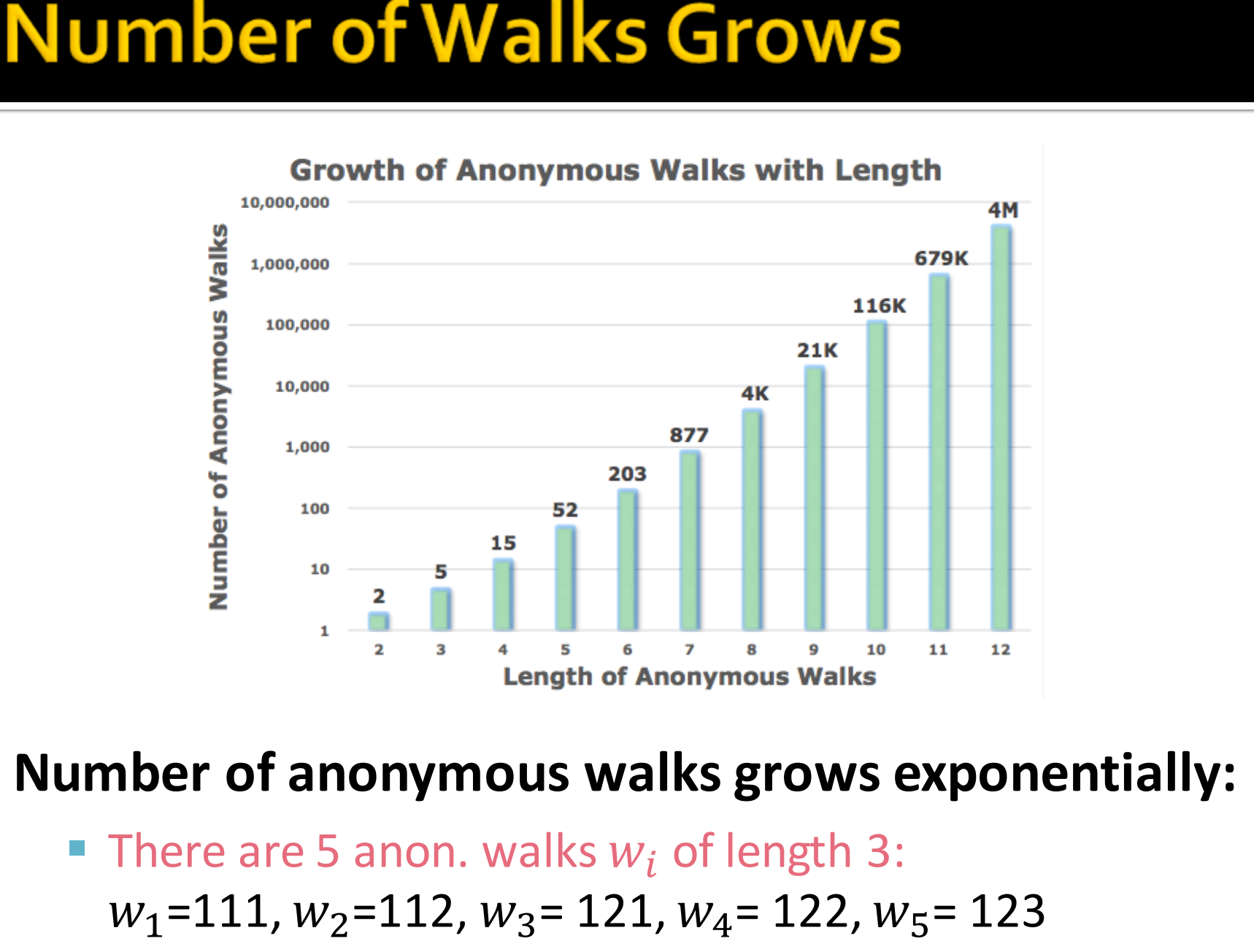
当l=12时,匿名游走w数目有4M。实际操作中,我们用采样来降低计算复杂度。
那么我们的m取多大?可用下式来估算:
其中, 是长度为 的匿名游走的总数。计算下上图例子,
7. New idea: Learn Walk Embeddings
不简单地用每次游走出现的次数的分数来表示匿名游走 ,而是学习匿名游走 的embedding 。
具体来说,(这跟NLP的doc2vec类似,后面再说)
这里, 是采样的匿名游走数目。
那么怎么embed walks?
实际流程如下 :
这样整个目标函数为:
其中, 是所有的walks数目。
对于式10,
每个步骤具体来说,
目标函数为:
这里, 是负采样得到所有匿名游走的embedding, 是图的embedding.
式12,表示当前walk t共现的可能性,分母是归一化因子,为了确保概率和为1。
其中 计算如下:
其中, 表示:
拼接后的embeddings一起输入到一个线性投影层,这就是整个式13的意义。
这里, 是可学习的参数。
Optimization:
方法2:引入一个”虚拟节点“来表示子图,然后再对其用node embedding。
3. 方法3: Anonymous Walk Embeddings
来源于 论文 Anonymous Walk Embeddings 。
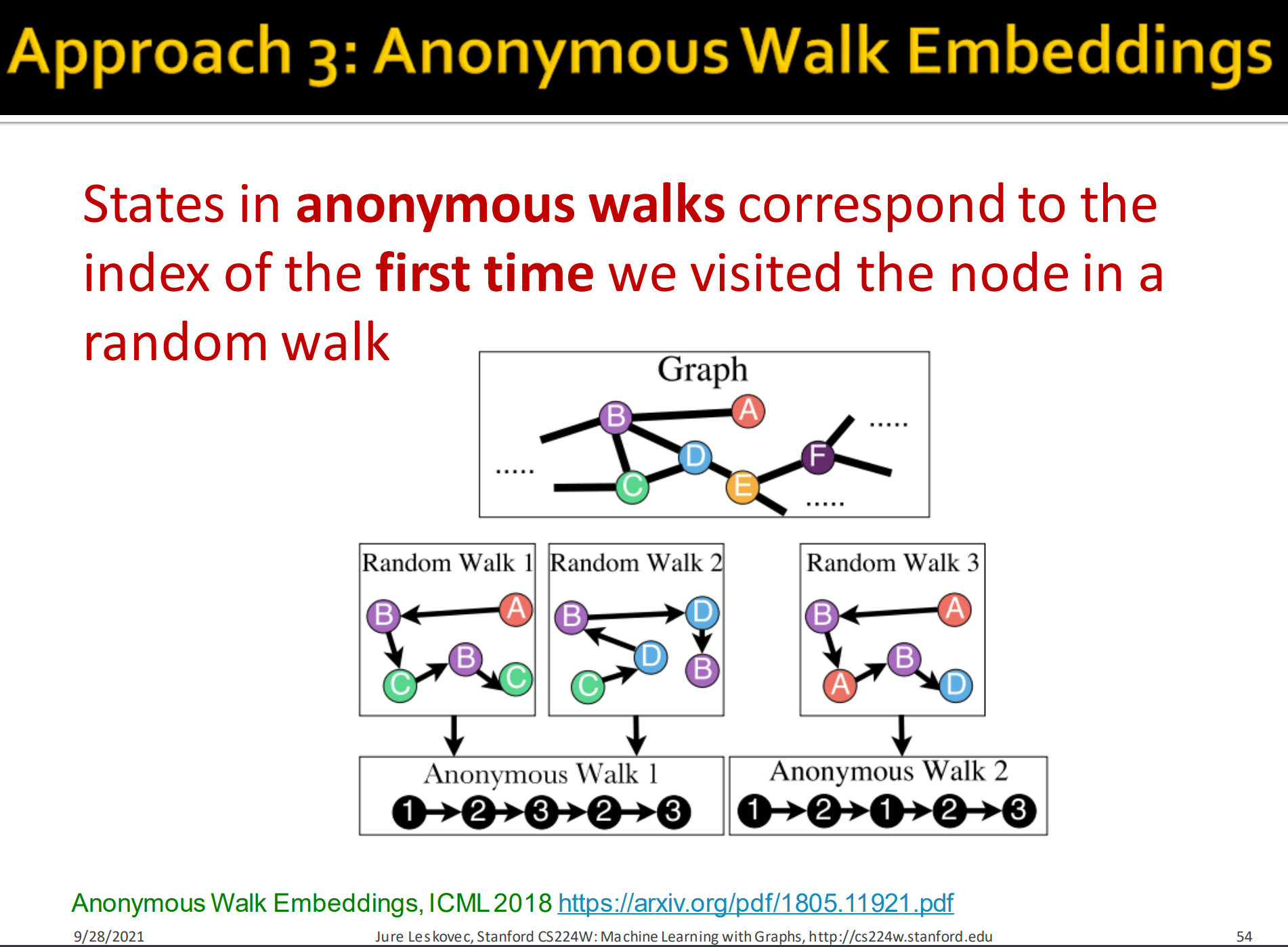
匿名游走的节点如果在先前出现过,则将此时的index设置为它第一次出现时的index,习惯性从1开始计数,每当遇到一个新的没有遇到过的节点,则自增state(index),即state的最大值等于这一条walk中存在的unique的节点数目。
—— Machine Learning with Graphs 之 Anonymous Walk Embeddings
对于例子:Random walk 整条walk的序列为 .
而Random walk 的序列为 。它们有一样的anonymous walk.
4. Number of Walks Grows
对于一个给定的图G,匿名游走得到的pattern数目跟路径长度l成指数成长。
路径长度为3的匿名游走pattern有5个。
5. Simple Use of Anonymous Walks
那么我们怎么利用匿名游走来嵌入整张图呢?
具体来说,就像上节中的Graphlet Degree Vector(GDV),我们先统计得到所有长度为l的匿名游走pattern,然后将图表示为获得pattern的频数或者概率。
举例来说,
13. Biased Random Walks
有偏的2阶随机游走探索网络邻居节点:
想法 :记住从哪来
14. node2vec algorithm
优点:线性时间复杂度(节点邻居树是固定的),三步都是独立的可以并行化。
其它随机游走想法:
15. Summary so far
11. How should we randomly walk?
node2vec 来自于论文 node2vec: Scalable Feature Learning for Networks ,想详细了解可以阅读下。
想法 :使用灵活,有偏的随机游走能平衡网络局部和全局信息。
两种典型的策略来定义给定节点u的邻域节点 :BFS 和DFS。
这是两种常见的图搜索算法,
下图是二者比较:
插入BFS和DFS :
有偏的固定长度随机游走R,在给定节点u的情况下能得到邻域节点
实际上, 。那么能不能采样任何节点获取负样本,或者只采样不在random walk上的节点?
答案是:实际操作中,对任何节点采样来获得负样本,高效性。正确的方式是只采样不在random wall上的节点。
9. Stochastic Gradient Descent
6. Feature Learning as Optimization
如果设置优化问题?
其中, 是某一策略R随机游走中节点u的邻居节点
解释下式3,对于节点u和其邻居节点, 表示给定节点u的情况下,让其邻居节点出现的概率最大。总的来说就是让图中所有节点,在映射函数f的作用下,使得每个节点u的邻居节点出现的概率的对数和最大。
7. Random Walk Optimization
怎么去做?
这里把 用v来表示了下。
为什么使用softmax? 因为节点v的和节点u相似度最大的,经过 处理后能更加区分出来。分母只是因为要归一化,概率和为1。
将式4和式5 结合起来 :
但实际做起来计算代价非常高,是图节点数的平方次复杂度。
那么我们能不能优化式6呢?
分母的归一化部分,有 的复杂度,如果能优化就会极大降低计算复杂度。
8.Negative Sampling
解决方法 : 负采样。
这里将softmax替换为sigmoid, 近似得到:
负采样就是将式7分母归一化部分中所有节点 替换为,随机采样得到的k个 负样本 ,即不在random walk上的样本。
负采样使得对数部分计算非常迅速。
5. Unsupervised Feature Learning
3. Random Walk Approaches for Node Embeddings
1. Notation
非线性函数用来生成预测概率 :
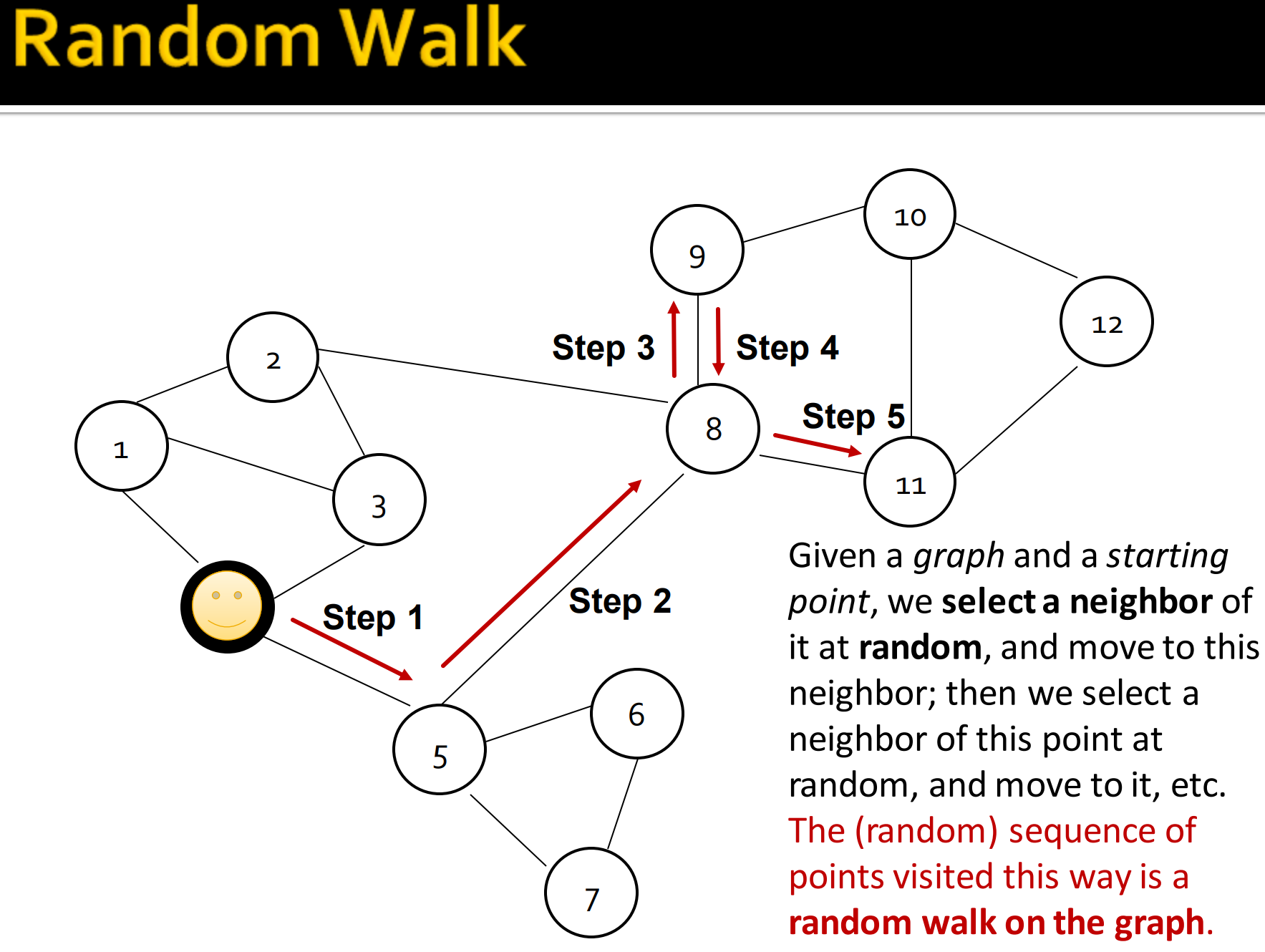
2. Random Walk
给定一个图和一个起点,我们可以随机选取一个邻居作为下一个游走的点,接下来我们继续选取下一个邻居游走,重复。这个访问的节点随机序列就是 图的随机游走 。
3. Random-Walk Embeddings
这里 表示 在图中一次随机游走时共同出现的概率。
4. Why Random Walks?
7. Note on Node Embeddings
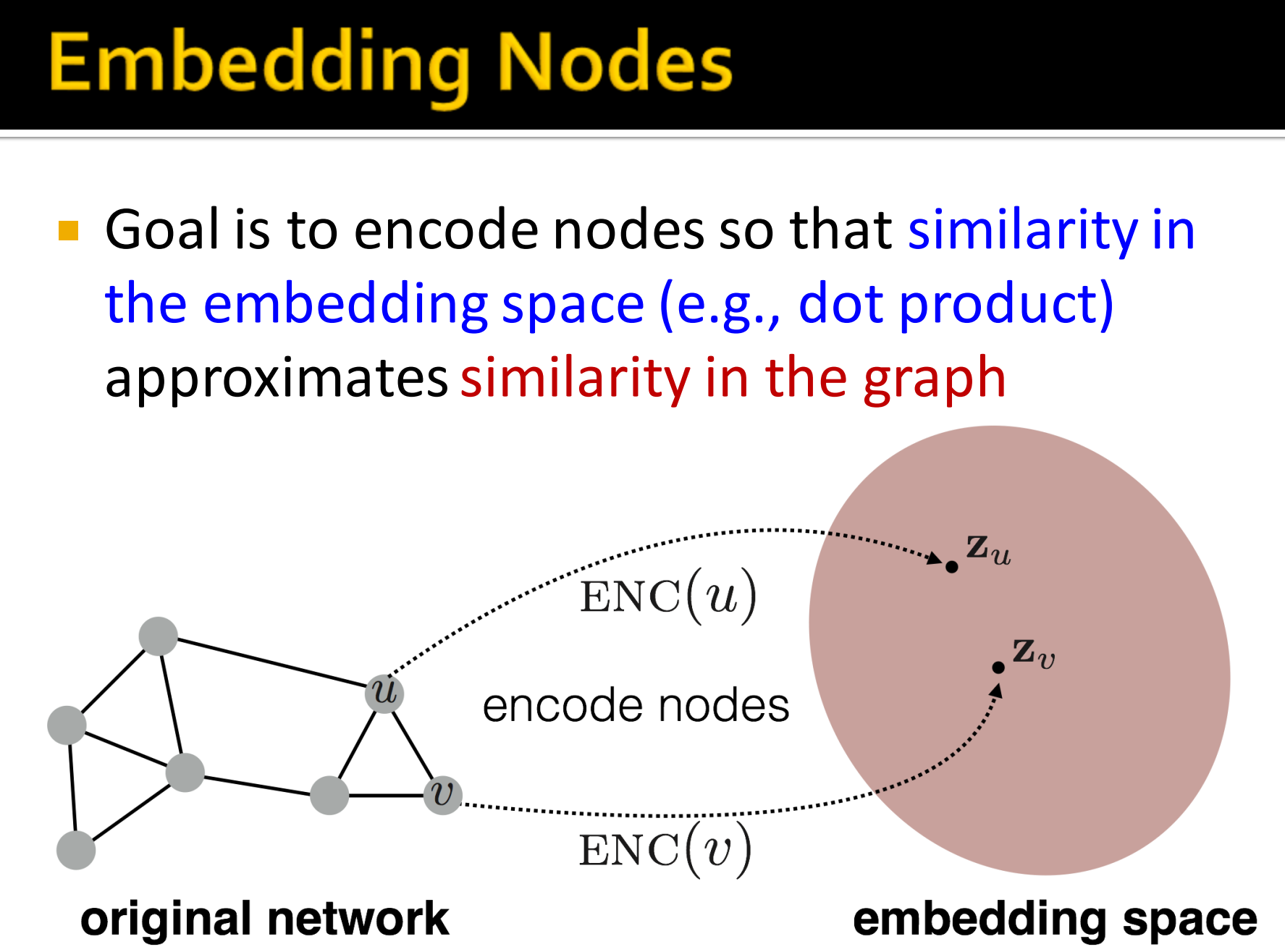
1. Embedding Nodes
目标是编码节点,以便embedding space中的相似度近似于图中的相似的。
如上图中,原始的网络中的邻居节点u、v ,编码到embedding空间后,对应的 也要相近。
节点的相似度计算:
其中, 就是接下来要讲的相似度计算函数,也是这里 表示的编码过程。
2. Learning Node Embeddings
3. Two Key Components
4. “Shallow” Encoding
最简单的编码方法: 编码器仅仅是一个embedding-lookup.
对于式2继续完善下:
其中, , 这是一个 的矩阵,每一列都是一个节点的embedding[通过学习/优化得到的]。怎么得到后面再说,要明确的是, 这是由 个节点的 维embedding构成的矩阵。
而 是一个指示向量,除了对应节点 那一列是1外其他都是0(one-hot向量)。这样从矩阵乘法来说,式3相乘的过程就是一个查表的过程。这也是为什么说这是一个embedding-lookup。下图图示就非常清楚了,注意一下这个矩阵 名字叫embedding matrix(NLP 同学相对很容易理解)。
学习或优化得到embedding matrix 的 方法 有: DeepWalk, node2vec 。
5. Framework Summary
Encoder+Decoder Framework
6. How to Define Node Similarity?
Node embedding 例子 :
下图是 DeepWalk: Online Learning of Social Representations 原图。Karate Club数据集在2D的投影,图中不同颜色的节点在embedding后也是相距比较远的,但同一颜色都是比较近的。(甚至有一种一一对应的映射感觉, 可能效果比较好)