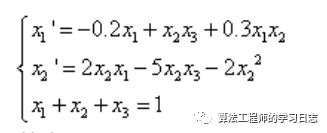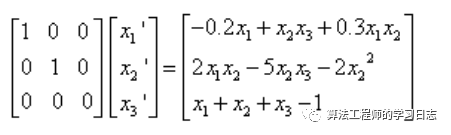什么是微分代数方程？

微分代数方程是一类微分方程，其中一个或多个因变量导数未出现在方程中。方程中出现的未包含其导数的变量称为代数变量，代数变量的存在意味着不能将这些方程记为显式形式 y′=f(t,y)。

ode15s 和 ode23t 求解器可以使用奇异质量矩阵 M(t,y)y′=f(t,y) 来解算微分指数为1的线性隐式问题，包括以下形式的半显式 DAE

y′0=f(t,y,z)

0 =g(t,y,z)

在此形式中，由于主对角线存在一个或多个零值，因此代数变量的存在会产生奇异质量矩阵。

默认情况下，求解器会自动检验质量矩阵的奇异性，以 检测 DAE 方程组。如果提前知道奇异性，则可将 odeset 的 MassSingular 选项设为 'yes'。对于 DAE，还可以使用 odeset 的 Ini ti alSlope 属性为求解器提供 y′(0) 的初始条件估计值。

举个例子

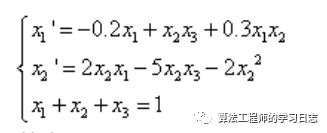
其中x1(0)=0.8;x2(0)=x3(0)=0.1;

1）方程写成DAE形式

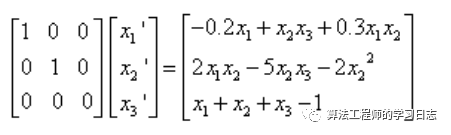
2） 编程 求解

%% 
clear
close all
odefun = @(t,x)[-0.2*x(1)+x(2)*x(3)+0.3*x(1)*x(2);
                2*x(1)*x(2)-5*x(2)*x(3)-2*x(2)^2;
                x(1)+x(2)+x(3)-1]; %微分方程
M = [1 0 0;0 1 0;0 0 0]; % 质量矩阵
options=odeset('mass',M); % 定义mass属性
x0=[0.8;0.1;0.1];
[t,x]=ode15s(odefun,[0 10],x0,options);
figure
plot(t,x(:,1),t,x(:,2),t,x(:,3))
grid on
legend('x1','x2','x3')
                        声明：本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人，不代表电子发烧友网立场。文章及其配图仅供工程师学习之用，如有内容侵权或者其他违规问题，请联系本站处理。
                                MATLAB仿真
            Matlab偏微分方程工具箱应用说明
    
Matlab偏微分方程工具箱应用说明1． 概述本文只给出该工具箱的函数列表，读者应先具备偏微分方程的基本知识，然后根据本文列出的函数查阅Matlab的帮助，便可掌握该工具箱的使用。2．
                发表于 09-22 15:26        
    
 本帖最后由 A670521546 于 2011-7-8 10:29 编辑 
常微分方程(ODEs)的MATLAB数值解法》偏微分方程(PDEs)的MATLAB数值解法》Z变换和差分
                发表于 07-08 08:42        
            【下载】《工程与科学数值方法的MATLAB实现（第2版）》
    
应用领域，具体包括求根与最优化、线性代数方程组的求解、曲线拟合、数值积分与微分以及常微分方程数值解。书中不但介绍了各类数值方法的基本原理和基于MAT
                发表于 08-28 17:27        
            含一般时延的高阶泛函微分方程的周期解
    
研究了一类含有“一般”时延的高阶泛函微分方程的周期解问题，将原方程化为等价的泛函微分方程，并利用该等价泛函微分方程的特征方程，得到了原
                发表于 02-28 17:07        
                •15次下载