NLP非线性优化第二步CasAdi Matlab库导出与部署
基于CasAdi可以实现四足机器人运动控制与跳跃,在 华北舵狗王:NLP非线性优化第一步Webots与CasAdi 中介绍了如何在Windows环境下部署与测试C++版本的代码,当然也实现了Webots下的仿真接口,从而加快了在仿真中快速验证相关算法,但实际上更多时候我们是 在Matlab环境下完成对优化问题的设计与开发 ,之后在实物样机中完成代码的部署,当然更合适的方法是完全在Ubuntu下直接采用Python或C++接口进行设计。不过目前我采用的方式是使用 Matlab完成复杂模型的验证 之后采用 CasADi代码生成功能导出相应的库 ,进一步完成在嵌入式系统中对库的调用,在输入数据后完成优化结果的获取,本文首先介绍了在Matlab环境下的代码如何转化成C++可以读取的库并在VS中调用,相比完全把Matlab中的优化问题重新写一遍会快很多,当然也存在很多限制。
1 Matlab下的库导出
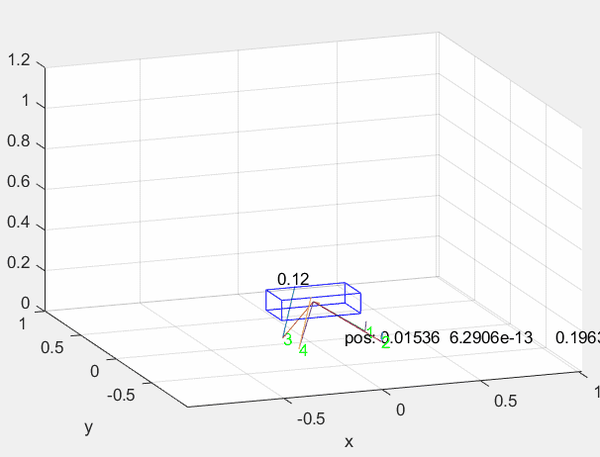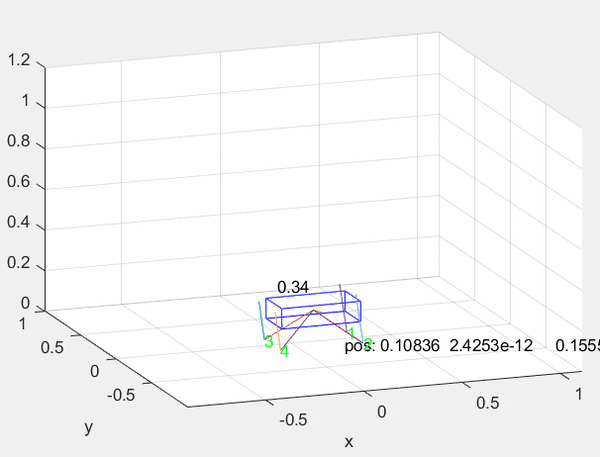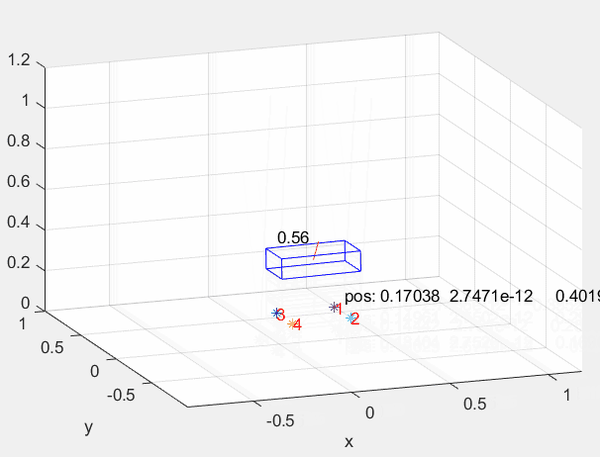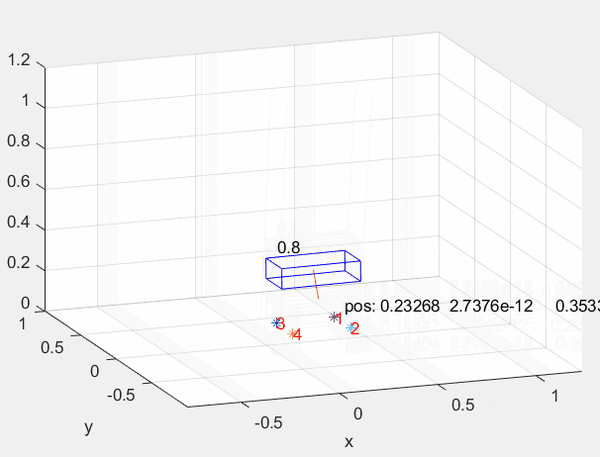
在构建一个优化问题后首先需要在Matlab中完成其库的生成和导出,这里移植了 四足机器人跳跃轨迹优化_Na-Cl的博客-CSDN博客 中的代码并采用其完成库导出与测试,直接运行后机器人完成一个跳跃规划:
机器人绘制函数:
%% 可视化函数
function cube_animate(X,time,foot_pos,swingstate,pre_contact,feetforce_used,fig,X_ref_mpc,path,mpcTra,Xtra,Polygon,View,dt,footSwingTrajectories)
%可视化函数 参考系为世界系 接触脚为绿色,摆动为红色
% X:需要绘制的状态向量
% time:显示在图上的时间
% foot_pos:落足点位置
% swingstate:摆动状态
% pre_contact:提前接触状态
% feetforce_used:控制力
% fig:窗口序号
% X_ref_mpc:参考轨迹
% path:跟踪路径
% 无
figure(fig);
clf; hold on; grid on; axis equal;
if ~isempty(View)
view(View(1), View(2))
view(-0, 0);%视角控制,目前为跟随机器人后方,从 45 方向看机器人 X(3)*180/pi
%绘制参考轨迹
if ~isempty(X_ref_mpc)
plot_temp=[];
for i=1:length(X_ref_mpc)/13
plot_temp=[plot_temp,X_ref_mpc((i-1)*13+4:(i-1)*13+6)];
plot3(plot_temp(1,:),plot_temp(2,:),plot_temp(3,:),'*');%绘制参考轨迹,'linewidth',6
%%绘制跟踪路径
if ~isempty(path)
plot3(path(:,1),path(:,2),ones(length(path(:,2)),1)*0.28);
if ~isempty(Polygon)
plot3(Polygon(1),Polygon(2),0,'o');
%绘制mpc预测的轨迹
if ~isempty(mpcTra)
plot_temp2=[];
for i=1:length(mpcTra)/12
plot_temp2=[plot_temp2,full(mpcTra((i-1)*12+4:(i-1)*12+6))];
plot3(plot_temp2(1,:),plot_temp2(2,:),plot_temp2(3,:),'o');
if ~isempty(Xtra)
plot3(Xtra(4,:),Xtra(5,:),Xtra(6,:));
R = rotz(X(3))*roty(X(2))*rotx(X(1));%旋转矩阵
plot3([X(4),X(4)+0.1*X(7)],[X(5),X(5)+0.1*X(8)],[X(6),X(6)+0.1*X(9)]);%当前角速度向量
plot3([X(4),X(4)+0.1*X(10)],[X(5),X(5)+0.1*X(11)],[X(6),X(6)+0.1*X(12)]);%当前速度向量
plot_cube(R,0.4,0.22,0.10,[X(4),X(5),X(6)]');%绘制机身 宽度长度
str=['pos: ',num2str(X(4:6)')];
str1=['rad: ',num2str(X(1:3)')];
text(X(4)+0.25,X(5)+0.25,X(6)-0.25,str);%标注POS/m
%text(X(4)-0.25,X(5)-0.25,X(6)+0.25,str1);%标注rpy/rad
text(X(4),X(5)+0.5,X(6),num2str(time*dt(1)));%标注时间/s
%绘制落脚点位置、r向量、力向量
for i=1:4
x_indx=3*(i-1)+1;
y_indx=3*(i-1)+2;
z_indx=3*(i-1)+3;
if ~isempty(footSwingTrajectories)
plot3(footSwingTrajectories(i).startPoint(1),footSwingTrajectories(i).startPoint(2),footSwingTrajectories(i).startPoint(3),'*','Color','r');
plot3(footSwingTrajectories(i).endPoint(1),footSwingTrajectories(i).endPoint(2),footSwingTrajectories(i).endPoint(3),'o','Color','b');
if swingstate(i)>0 && pre_contact(i)~=1%边缘切换信号 摆动
text(foot_pos(x_indx),foot_pos(y_indx),foot_pos(z_indx),num2str(i),'Color','red');%在落点标注脚序号 摆动用红色
plot3(foot_pos(x_indx),foot_pos(y_indx),foot_pos(z_indx),'*');%绘制空中足端位置
plot3([foot_pos(x_indx),foot_pos(x_indx)+0.01*feetforce_used(x_indx)],...
[foot_pos(y_indx),foot_pos(y_indx)+0.01*feetforce_used(y_indx)],...
[foot_pos(z_indx),foot_pos(z_indx)+0.01*feetforce_used(z_indx)]);
text(foot_pos(x_indx),foot_pos(y_indx),foot_pos(z_indx),num2str(i),'Color','green');%在落点标注脚序号 接触用绿色
plot3([foot_pos(x_indx),foot_pos(x_indx)+0.01*feetforce_used(x_indx)],...
[foot_pos(y_indx),foot_pos(y_indx)+0.01*feetforce_used(y_indx)],...
[foot_pos(z_indx),foot_pos(z_indx)+0.01*feetforce_used(z_indx)]);
plot3([X(4),foot_pos(x_indx)],[X(5),foot_pos(y_indx)],[X(6),foot_pos(z_indx)]);%ri
axis([X(4)-1,X(4)+1,X(5)-1,X(5)+1,0,1.2]);%坐标系范围 以当前机身为中心
xlabel('x');ylabel('y');zlabel('z');%规范x,y,z坐标轴刻度范围,及在各自坐标轴上标注字母x,y,z
drawnow;
function plot_cube(R, a, b, c,pos)
x = [-1, 1, 1, -1, -1, 1, 1, -1] * a/2;
y = [-1, -1, 1, 1, -1, -1, 1, 1] * b/2;
z = [-1, -1, -1, -1, 1, 1, 1, 1] * c/2;
P = R * [x; y; z]+pos;
order = [1, 2, 3, 4, 1, 5, 6, 7, 8, 5, 6, 2, 3, 7, 8, 4];
plot3(P(1, order), P(2, order), P(3, order), 'b');
%% 工具函数
function rotxm=rotx(theta)
s=sin(theta);
c=cos(theta);
% rotxm=[1,0,0;
% 0,c,s
% 0,-s c]';
rotxm=[1,0,0;
0,c,-s
0,s c];
function rotym=roty(theta)
s=sin(theta);
c=cos(theta);
% rotym =[c,0,-s;
% 0,1,0;
% s,0,c]';
rotym =[c,0,s;
0,1,0;
-s,0,c];
function rotzm=rotz(theta)
s=sin(theta);
c=cos(theta);
% rotzm=[c,s,0;
% -s,c,0;
% 0,0,1]';
rotzm=[c,-s,0;
s,c,0;
0,0,1];
function R=rotsb(theta)
% R=rotx(theta(1))*roty(theta(2))*rotz(theta(3));
R=rotz(theta(3))*roty(theta(2))*rotx(theta(1));
function s=Skew(in)
s=zeros(3,3);
s(1,2)=-in(3);
s(1,3)=in(2);
s(2,3)=-in(1);
s(2,1)=in(3);
s(3,1)=-in(2);
s(3,2)=in(1);
% s = [0 -in(3) in(2);
% in(3) 0 -in(1);
% -in(2) in(1) 0];
主函数:
clc;
close all;
clear;
warning off
addpath('C:/casadi-windows-matlabR2016a-v3.5.5')
import casadi.*
%0 1腿号
%------------------行为规划--------------------
Sect=4;% 相序数量
N = 40; % 总分段比例 多相序为增加MPC控制精度应该 计算出个阶段末端状态作为约束 分段进行MPC控制 必须是偶数
T = 0.8; % 总时间长度 可以改成按时间规划相序
dt_val = repmat(T/(N),1,N)';%每个相序的分段比例
gen_lib= 0;
Fmax= 128;
max_jump_z=0.8;%最高跳跃高度 但是不能保证一定跳跃到
min_damp_z=0.15;%最低限制高度
max_lift_spdz=3.5;%最大离地速度
z_init=0.2;%起始站立高度
world.mu=0.5;%摩擦系数
q_init_val = [0 0 0 ...
0 0 z_init]';%初始状态 rpy xyz
qd_init_val = [0 0 0 0 0 0]';
q_term_ref = [1*pi*0 -22/57.3*0 pi*0 ...
0.4+1e-5 0 0.1 ]';%终端位置 rpy xyz
qd_term_ref = [0 0 0, 0 0 0]';
%Phase_duty=[int16(N/Sect*0.2) int16(N/Sect*0.3) int16(N/Sect*0.49) int16(N/Sect*0.01)];%相序百分比 下蹲 蹬腿 腾空 缓冲
cs_val = [repmat([1 1 1 1]', 1, 15) repmat([1 1 1 1]', 1, 5) repmat([0 0 0 0]', 1, 19) repmat([0 0 0 0]', 1, 1)]';%MPCtable相序
%接触状态
%cs_TD_val = zeros(Sect,N-1)';
%% %状态的权重
weight.QX = [10 10 10, 10 10 10, 10 10 10, 10 10 10 ]';%系统状态代价的权重 轨迹
weight.QN = [10 10 10, 50 50 150, 10 10 10, 10 10 10 ]';%终端代价
weight.Qc = [0.001 0.001 0.001]';
weight.Qf = [0.0001 0.0001 0.001]';
%% %物理参数
Body.m = 5+0.25*8;%机器人质量
%机身惯量
I=[0.059150 0.101150 0.046240]*4;
Body.Ib = [I(1) 0 0;%roll
0 I(2) 0;%pit
0 0 I(3) ];%yaw 转动惯量矩阵
Body.length_body=0.34;
Body.width_body=0.26;
%0 1腿号
Body.hipPos=[Body.length_body/2, Body.length_body/2, -Body.length_body/2, -Body.length_body/2;%髋关节位置
Body.width_body/2, -Body.width_body/2, Body.width_body/2, -Body.width_body/2;
0, 0, 0, 0];
endPos=[0, 0, 0, 0;%足端跨关节位置 %初始化足端位置
0, 0, 0, 0;
-z_init, -z_init, -z_init, -z_init];
world.g = 9.8;%重力加速度
%% 构造微分方程
Xk=SX.sym('Xk', 12, 1);%cassis 符号类
n_state=size(Xk,1);
Fk=SX.sym('Uk', 12, 1);
n_F=size(Fk,1);
Rk=SX.sym('Rk', 12, 1);
n_r=size(Rk,1);
%% 计算微分方程
I3=eye(3);%单位矩阵
Rbody=rotsb(Xk(1:3));
cy = cos(Xk(3));
sy = sin(Xk(3));
cp = cos(Xk(2));
sp = sin(Xk(2));
R_yaw =[cy sy 0;
-sy cy 0;
0 0 1];%世界到机身
R_w=[cy/cp,sy/cp,0;
-sy,cy,0;
cy*sp/cp,sy*sp/cp,1];
Ig = Rbody*Body.Ib*Rbody';
Ig_inv=Ig\I3;
%单刚体动力学模型
A = [zeros(3) zeros(3) R_yaw zeros(3) ;
zeros(3) zeros(3) zeros(3) I3 ;
zeros(3) zeros(3) zeros(3) zeros(3);
zeros(3) zeros(3) zeros(3) zeros(3) ;
];%状态矩阵
% AA=A;
% AA(1:3,7:9)=R_w;
B=[ zeros(3) zeros(3) zeros(3) zeros(3);
zeros(3) zeros(3) zeros(3) zeros(3);
Ig_inv*Skew(Rk(1:3)) Ig_inv*Skew(Rk(4:6)) Ig_inv*Skew(Rk(7:9)) Ig_inv*Skew(Rk(10:12));
I3/Body.m I3/Body.m I3/Body.m I3/Body.m;];%控制矩阵
g=zeros(12,1);
g(12)=-world.g;%扩展一维度重力加速度
dotX=A*Xk+B*Fk+g;%构造微分动力学的符号方程
%% 定义函数
f=Function('f',{Xk;Fk;Rk},{dotX},{'input_states','control_inputs','foot_input'},{'dotX'});
% X_init = [0;0.0;0; 0.0;0.0;0.5 ;0;0;0; 0;0;0;-9.8];%初始状态变量
% f(X_init,zeros(12,1),zeros(12,1))%测试函数正常否
%% 构造代价和约束 变量定义
X = SX.sym('X', n_state, N+1); % N+1步状态
F = SX.sym('F', n_F, N); % N步内的控制 力控制
r = SX.sym('r', n_r, N); % N步内的控制 足端位置控制
RefX = SX.sym('RefX', n_state, N+1); % N步内的控制输出
RefF = SX.sym('RefF', n_F, N); % N步内的控制输出
Refr = SX.sym('Refr', n_r, N); % N步内的控制输出
ContactState=SX.sym('ConState', 4, N);
obj=0;
%% 构造代价和约束 变量定义
mu_inv = 1.0/world.mu;
%摩擦约束
f_block =[ mu_inv, 0, -1.0;
-mu_inv, 0, -1.0;
0, mu_inv, -1.0;
0, -mu_inv, -1.0;];
kin_box_x = 0.15;%运动学约束
kin_box_y = 0.15;
kin_box_z = 0.3;%腿最长
Kin_block =[ 1, 0, 0,-kin_box_x;%髋关节坐标系
-1, 0, 0,-kin_box_x;
0, 1, 0,-kin_box_y;
0, -1, 0,-kin_box_y;
0, 0, 1,-min_damp_z;%腿最短
0, 0, -1,-kin_box_z];
endPos_Body=Body.hipPos+endPos;
Phip_swing=reshape(endPos_Body,[],1);
%% 约束暂存变量定义 %初态约束
%初态约束
defect_init=RefX(:,1)-X(:,1);%12*1 eq
defect_state=SX.zeros(12*(N+1),1);%12(N+1)*1 eq
defect_FootOnGround=SX.zeros(4*(N),1);%4(N)*1 eq
defect_footStance=SX.zeros(12*(N),1);%(3*4)(N)*1 eq
n_equa_c=12+12*(N+1)+4*(N)+12*(N);
defect_legLimits=SX.zeros(24*(N),1);%(4*6)(N)*1
defect_footforce=SX.zeros(16*(N),1);%(4*4)(N)*1 xy摩擦约束4个
defect_ForceNormal=SX.zeros(N,1);% (N)*1
defect_footswing=SX.zeros(4*(N),1);%4(N)*1
n_inequa_c=24*(N)+16*(N)+N+4*(N);
%% 约束和代价计算
for k = 1:N
%% 代价计算
Xk=X(:,k);
Fk=F(:,k);
rk=r(:,k);
Pk=repmat(Xk(4:6),4,1)+rk;
ContactStatek=ContactState(:,k);
dtk=dt_val(k);
X_err = Xk - RefX(:,k); % 基座状态误差
pf_err = repmat(Xk(4:6),4,1) + Phip_swing - Pk; % 悬空时约束foot位置 不影响跳跃 只影响最终足端状态输出的结果
U_err = Fk - RefF(:,k); % GRF 误差
obj = obj + (X_err'*diag(weight.QX)*X_err+... % 误差求和
pf_err'*diag(repmat(weight.Qc,4,1))*pf_err+...
U_err'*diag(repmat(weight.Qf,4,1))*U_err)*dtk;
%% 约束计算
%状态约束
%runge kutta method
% k1 = f(Xk,Fk,Pk); % new
% k2 = f(Xk + dtk/2*k1,Fk,Pk); % new
% k3 = f(Xk + dtk/2*k2,Fk,Pk); % new
% k4 = f(Xk + dtk*k3,Fk,Pk); % new
% st_next_RK4=Xk +dtk/6*(k1+2*k2+2*k3+k4); % new
% defect_state((k-1)*12+1:(k-1)*12+12)=X(:,k+1)-(st_next_RK4);
defect_state((k-1)*12+1:(k-1)*12+12)=X(:,k+1)-(Xk+f(Xk,Fk,rk)*dtk);
%法向力大于0 不等式
defect_ForceNormal(k)=-dot(Fk,repmat([0;0;1],4,1));
%结合法向力大于0,摩擦约束来约束摆动中力为0 和最大力 不等式
defect_footswing((k-1)*4+1:(k-1)*4+4)=Fk([3,6,9,12])-ContactStatek.*repmat(1000,4,1);
for leg=1:4
xyz_idx = 3*(leg-1)+1:3*(leg-1)+3;
%脚在地上约束 0是此时地面高度等式
defect_FootOnGround((k-1)*4+leg)=ContactStatek(leg)*Pk(3*(leg-1)+3);
%限制腿长 限制范围不等式
Rbody=rotsb(Xk(1:3));
endWorld=Rbody*endPos_Body+Xk(4:6);%全局足端位置
p_rel = (Pk(xyz_idx) - endWorld(:,leg));%hip->足端 足端矢量
defect_legLimits((k-1)*24+(leg-1)*6+1:(k-1)*24+(leg-1)*6+6)= Kin_block*[p_rel;1];%运动学约束
%接触中脚不滑动
if (k < N)
Pk1=repmat(X(4:6,k+1),4,1)+r(:,k+1);
defect_footStance((k-1)*12+(leg-1)*3+1:(k-1)*12+(leg-1)*3+3)=ContactStatek(leg)*(Pk1(xyz_idx)-Pk(xyz_idx));
%摩擦约束 不等式
defect_footforce((k-1)*16+(leg-1)*4+1:(k-1)*16+(leg-1)*4+4)=f_block*Fk(xyz_idx);
%% 约束生成
g=[defect_init;defect_state;defect_FootOnGround;defect_footStance;...
defect_legLimits;defect_footforce;defect_ForceNormal;defect_footswing];
display_str=['等式约束数量',num2str(n_equa_c),' 不等式约束数量',num2str(n_inequa_c)];
disp(display_str);
%% 终端 cost
X_err = X(:,end)-RefX(:,end); % 终端 cost
obj = obj + X_err'*diag(weight.QN)*X_err;
%% 构造问题和问题变量
OPT_variables = [reshape(X,n_state*(N+1),1);reshape(F,n_F*N,1);reshape(r,n_r*N,1)];
OPT_Param = [reshape(RefX,n_state*(N+1),1);reshape(RefF,n_F*N,1);reshape(Refr,n_r*N,1);reshape(ContactState,4*N,1)];
nlp_prob =struct('f', obj, 'x',OPT_variables,'p',OPT_Param, 'g',g );
%% 优化设置
opts_setting.expand =true;
opts_setting.ipopt.max_iter=1500;
opts_setting.ipopt.print_level=0;
opts_setting.ipopt.acceptable_tol=1e-4;
opts_setting.ipopt.acceptable_obj_change_tol=1e-6;
opts_setting.ipopt.tol=1e-4;
opts_setting.ipopt.nlp_scaling_method='gradient-based';
opts_setting.ipopt.constr_viol_tol=1e-3;
opts_setting.ipopt.fixed_variable_treatment='relax_bounds';
%% 构造求解器
if gen_lib
solver = nlpsol('solver', 'ipopt', nlp_prob,opts_setting);%可以在线修改足端位置
solver = casadi.nlpsol('solver', 'ipopt', ['nlp.so'],opts_setting);%不需要nlp_prob
% tic;
% [status1,cmdout] = system(command,'-echo'); % compile the file % takes a few minutes
% t_comp=toc;
% fprintf('Done compiling in :%.2f s\n',t_comp)
%% 约束上下界面 args
args.lbg(1:n_equa_c) = 0; % -1e-20 % Equality constraints
args.ubg(1:n_equa_c) = 0; % 1e-20 % Equality constraints
args.lbg(n_equa_c+1 : n_equa_c+ n_inequa_c) = -inf; % inequality constraints
args.ubg(n_equa_c+1 : n_equa_c+ n_inequa_c) = 0; % inequality constraints
%% 决策变量上下界面 args
%% 状态上边界
tempub=[Body.m*world.g*world.mu*6; Body.m*world.g*world.mu*6 ;Fmax];
args.ubx=[];
UBx=[pi*3*ones(3,1);10*ones(2,1);1;...
pi*3*ones(3,1);40*ones(3,1)];%状态上届 约束跳的最高高度
UBx(6)=max_jump_z;
UBx(12)=max_lift_spdz;
UBx=repmat(UBx,N+1,1);
UBf=[tempub;tempub;tempub;tempub];
UBf=repmat(UBf,N,1);
UBp=repmat([0.4;0.4;inf],4,1);
UBp=repmat(UBp,N,1);
args.ubx=[args.ubx;UBx;UBf;UBp];
%% 状态下边界
templb=[-Body.m*world.g*world.mu*6; -Body.m*world.g*world.mu*6 ;0];%力状态
args.lbx=[];
LBx=[-pi*3*ones(3,1);-10*ones(2,1);min_damp_z;...
-pi*3*ones(3,1);-40*ones(3,1)];%状态下界
LBx=repmat(LBx,N+1,1);
LBf=[templb;templb;templb;templb];
LBf=repmat(LBf,N,1);
LBp=repmat([-0.4;-0.4;-inf],4,1);
LBp=repmat(LBp,N,1);
args.lbx=[args.lbx;LBx;LBf;LBp];
% c_init_val = repmat(q_init_val(4:6),4,1)+...
% diag([1 1 1, 1 -1 1, -1 1 1, -1 -1 1])*repmat([0.2 0.1 -q_init_val(6)],1,4)';
c_ref = diag([1 1 1, 1 -1 1, -1 1 1, -1 -1 1])*repmat([0.2 0.1 -z_init],1,4)';%初始化足端位置 --------------------足端位置
f_ref = zeros(12,1);
%% set parameter values 设定期望运动轨迹
for i = 1:6%对状态线性插值
Xref_val(i,:) = linspace(q_init_val(i),q_term_ref(i),N+1);%决定轨迹末端位置
Xref_val(6+i,:) = linspace(qd_init_val(i),qd_term_ref(i),N+1);
% Z向抛物线
a=[Xref_val(4,1),Xref_val(4,N/2),Xref_val(4,N)];%x
b=[q_init_val(6),q_term_ref(6),q_init_val(6)+0.0];%z
Xref_val(6,:) =interp1(a,b,Xref_val(4,:),'spline'); %高度方向做Spline插值
Uref_val=zeros(24,N);
r_ref=zeros(12,N);
for leg = 1:4
for xyz = 1:3
Uref_val(3*(leg-1)+xyz,:)= Xref_val(xyz+3,1:end-1) +c_ref(3*(leg-1)+xyz);%F
r_ref(3*(leg-1)+xyz,:)= c_ref(3*(leg-1)+xyz);%
Uref_val(12+3*(leg-1)+xyz,:) = f_ref(xyz).*ones(1,N);%P
if(1)%线性插值
for i = 1:6
Xref_val(i,:) = linspace(q_init_val(i),q_term_ref(i),N+1);
Xref_val(6+i,:) = linspace(qd_init_val(i),qd_term_ref(i),N+1);
for leg = 1:4
for xyz = 1:3
Uref_val(3*(leg-1)+xyz,:) = Xref_val(xyz,1:end-1) + c_ref(3*(leg-1)+xyz);
Uref_val(12+3*(leg-1)+xyz,:) = f_ref(xyz).*ones(1,N);
F_ref=Uref_val(13:24,:);
args.p=[reshape(Xref_val,n_state*(N+1),1);reshape(F_ref,n_F*N,1);reshape(r_ref,n_r*N,1);reshape(cs_val',4*N,1)];%送入了轨迹约束 相序约束
args.x0=[reshape(Xref_val,n_state*(N+1),1);reshape(F_ref,n_F*N,1);reshape(r_ref,n_r*N,1)];%系统初始状态
%-----------求解
sol=solver('x0',args.x0,'lbx', args.lbx,'ubx', args.ubx,'lbg', args.lbg,'ubg', args.ubg,'p',args.p);%调用求解器 输入数据
x_li=sol.x(1:n_state*(N+1));
x_li=reshape(full(x_li),n_state,(N+1));%质心世界下的位置
f_li=sol.x(n_state*(N+1)+1:n_state*(N+1)+n_F*N);
f_li=reshape(full(f_li),n_F,N);%足端力
r_li=sol.x(n_state*(N+1)+n_F*N+1:n_state*(N+1)+n_F*N+n_r*N);
r_li=reshape(full(r_li),n_F,N);%机体下足端位置
p_li=r_li+repmat(x_li(4:6,1:end-1),4,1);%世界足端位置
%------------导出
if gen_lib
solver = nlpsol('solver','ipopt',nlp_prob,opts_setting);
disp('Solver without Simple Bounds generated');
c_file_name = 'nlp';
disp('Generating c code');
opts = struct('main', false,...
'mex', true);
solver.generate_dependencies([c_file_name,'.c'],opts);% generete helper functions
disp('Done generating .c file');
disp('Compiling .c file (takes ~15 minutes)');
command = ['gcc -fPIC -shared -O0 ', c_file_name,'.c -o ',c_file_name,'.so']; %00-35s o1-229.17
[status1,cmdout] = system(command,'-echo'); % compile the file % takes a few minutes
t_comp=toc;
fprintf('Done compiling in :%.2f s\n',t_comp)
%------------------------记录
writematrix(x_li,'x_li.csv');
writematrix(f_li,'f_li.csv');
%------------------------绘图
figure(1);
subplot(2,1,1)
plot(x_li(6,:));grid on;%绘制质心运行轨迹
subplot(2,1,2)
plot(x_li(12,:));grid on;%绘制质心运行轨迹 RPY XYZ DRPY DXYZ
figure(2);
subplot(4,1,1)
plot(f_li(3,:));%绘制足端力
hold on; grid on;
subplot(4,1,2)
plot(f_li(6,:));%绘制足端力
hold on; grid on;
subplot(4,1,3)
plot(f_li(9,:));%绘制足端力
hold on; grid on;
subplot(4,1,4)
plot(f_li(12,:));%绘制足端力
grid on;
figure(5);
subplot(4,1,1)
plot(f_li(1,:));%绘制足端力
hold on; grid on;
subplot(4,1,2)
plot(f_li(4,:));%绘制足端力
hold on; grid on;
subplot(4,1,3)
plot(f_li(7,:));%绘制足端力
hold on; grid on;
subplot(4,1,4)
plot(f_li(10,:));%绘制足端力
grid on;
figure(3);
pic_num = 1;%保存gif用
time=['NLP','_',datestr(datetime('now'),'yyyy-mm-dd-HH-MM'),'_Animated.gif'];
for i=1:N
cube_animate(x_li(:,i),i,p_li(:,i),~cs_val(i,:),[0;0;0;0],...
f_li(:,i),3,[],[],[],[],[],[-20,14],dt_val,[]);
pause(0.01);%影响绘画
%% 工具函数
function rotxm=rotx(theta)
s=sin(theta);
c=cos(theta);
% rotxm=[1,0,0;
% 0,c,s
% 0,-s c]';
rotxm=[1,0,0;
0,c,-s
0,s c];
function rotym=roty(theta)
s=sin(theta);
c=cos(theta);
% rotym =[c,0,-s;
% 0,1,0;
% s,0,c]';
rotym =[c,0,s;
0,1,0;
-s,0,c];
function rotzm=rotz(theta)
s=sin(theta);
c=cos(theta);
% rotzm=[c,s,0;
% -s,c,0;
% 0,0,1]';
rotzm=[c,-s,0;
s,c,0;
0,0,1];
function R=rotsb(theta)%构造旋转矩阵
% R=rotx(theta(1))*roty(theta(2))*rotz(theta(3));
R=rotz(theta(3))*roty(theta(2))*rotx(theta(1));
function s=Skew(in)
s = [0 -in(3) in(2);
in(3) 0 -in(1);
-in(2) in(1) 0];
end在代码中可以看到,在 solver之前详细描述了整个轨迹优化问题 ,包括代价、待优化参数等,而在之后确定了各个部分的约束矩阵以及轨迹初值,之后输入相关轨迹参数完成优化最终取出所需要的值,为gen_lib赋值为1生成so库:
casadi会自动调用内部接口将solver建立是整个函数转换成对应的 c文件并编译为库 ,这里可以指定gcc优化等级如果优化等级越高编译的时间也越长。最终编译无误后会在目录下生成对应的nlp.so文件。这里修改gen_lib标志位后可以看到solver建立将直接采用导出的库,最终的结果和用代码书写的优化结果是一样的:
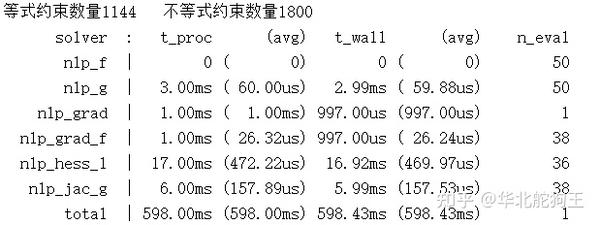
2 C++下对库的调用与Matlab接口转化
基于之前C++成功运行NLP例程的基础,原理上我们只需要向Matlab中一样 调用nlp.so库输入对应的数据 就可以获取相应的优化结果, 目前这一块在官方网站上是没有任何详细教程的 ,通过查看casadi自带的例程不断测试,这边给出一个 可运行的模板 ,里面详细介绍了如何将Matlab下的部分矩阵和数据接口采用 DM类型转化为CasADi可以识别的数据 ,实际上C++中的描述与Matlab中是一一对应的,下面主要介绍下在C++中我们常用的一些书写形式,特别是matlab中矩阵截取,建立数组等操作:
(1)vertcat行矩阵构建
该命令可以实现像matlab中一样用排列的数据构建一个行矩阵,以我们MPC Table为例其为数据的转置,则C++中可以写成DM Td_f1 = DM::vertcat({ 1, 1, 1, 1 });
cs_val = [repmat([1 1 1 1]', 1, 15) repmat([1 1 1 1]', 1, 5) repmat([0 0 0 0]', 1, 19) repmat([0 0 0 0]', 1, 1)]';%MPCtable相序 (2)repmat 复制和平铺矩阵
在matlab中repmat即将一个矩阵按块评判为对应的新矩阵,以cs_val = [repmat([1 1 1 1]', 1, 15) 为例其将[1 1 1 1]'平铺为了15列相同的数据,则C++可以写成DM Phase1 = DM::repmat(Td_f1, 1, 15);
(3)horzcat列矩阵构建
该命令与vertcat类似不过是按列组成一个新矩阵以cs_val为例,c++写成:
DM cs_val=DM::horzcat({ Phase1,Phase2,Phase3,Phase4}).T();最后的T()对应Matlab中的转置;
(4)新建一个固定尺寸矩阵
采用DM命令新建一个矩阵,矩阵维度可以在Matlab中中断查看,DM lbg = DM(1, 2944);创建单位矩阵DM::ones(3, 1)即建立了一个3X1的全为1矩阵;
(5)reshape按矩阵维度重构矩阵
对应matlab中reshape,C++中可以写成:DM p_Xref_val=DM::reshape(Xref_val, 12*(N + 1), 1);
(6)截取矩阵
在matlab中我们常用A[0 : 12 * (N + 1)]截取某个向量中一部分数据,则在C++可以写成:
DM A_s= A(casadi::Slice(0,12 * (N + 1)));3. C++下库的调用与优化结果获取
采用上面的描述方法基于DM类型可以非常快速的把Matlab中的代码改写为C++,由于nlp.so已经完全包含了整个轨迹优化公式和代价,在调用是只需要向其中输入matlab中对应的 初值x0、等式与不等式约束,以及p优化轨迹的始末参数 :
%-----------求解
sol=solver('x0',args.x0,'lbx', args.lbx,'ubx', args.ubx,'lbg', args.lbg,'ubg', args.ubg,'p',args.p);%调用求解器 输入数据因此在C++接口中基于DM数据类型向arg字段送入对应数据:
arg["lbx"] = lbx;
arg["ubx"] = ubx;
arg["lbg"] = lbg;
arg["ubg"] = ubg;
arg["x0"] = x0;
arg["p"] = p;
// Solve the NLP
res = solver(arg);//送入优化器则res即包含了整个优化结果sol的一个超大数组输出,其具体对应关系仍然通过 查看matlab中的结果和读取方式 ,采用DM读取后转换为Vector类型:
Matlab:
x_li=sol.x(1:n_state*(N+1));
x_li=reshape(full(x_li),n_state,(N+1));%质心世界下的位置
f_li=sol.x(n_state*(N+1)+1:n_state*(N+1)+n_F*N);
f_li=reshape(full(f_li),n_F,N);%足端力
r_li=sol.x(n_state*(N+1)+n_F*N+1:n_state*(N+1)+n_F*N+n_r*N);
r_li=reshape(full(r_li),n_F,N);%机体下足端位置
p_li=r_li+repmat(x_li(4:6,1:end-1),4,1);%世界足端位置C++:
vector<float> w_opt(res.at("x"));//读取优化结果
float x_li_all[12][40];//系统状态轨迹输出
for (int i = 0; i <40; i++) {
for (int j = 0; j < 12; j++) {
x_li_all[j][i] = w_opt[i*12+j];
//printf("pos[%d] Pos:%f %f | Spd=%f %f\n", i, x_li_all[3][i], x_li_all[5][i], x_li_all[9][i], x_li_all[11][i]);
float f_lit[12][40];//力输出
for (int i = 0; i < 40; i++) {
for (int j = 0; j < 12; j++) {
f_lit[j][i] = w_opt[i * 12 + j+ 12 * (N + 1) + 1 - 1];
//printf("ff[%d] x=%f %f z=%f %f \n", i, f_lit[0][i], f_lit[3][i], f_lit[2][i], f_lit[5][i]);
}则将该轨迹存储在数组中输出至 WBC或轨迹跟踪控制器即完成对跳跃运动的输出 ,可以看到最终在Webots里的优化时间会有变化:
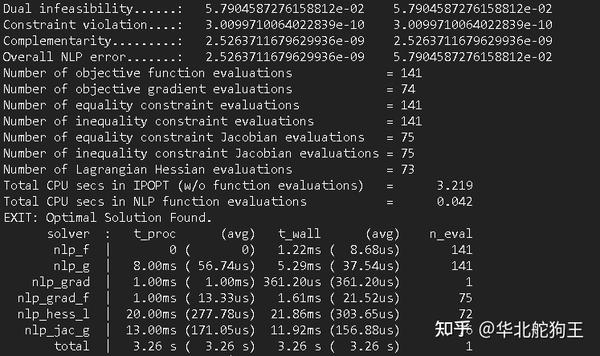

则通过修改始末状态可以实现 在线优化迭代的目的 ,最后的问题就是将这样的框架部署到嵌入式系统中:
//%初始状态 rpy xyz
float q_init_val[6] = { 0 ,0 ,0 ,0, 0, z_init };
float qd_init_val[6] = { 0, 0, 0, 0, 0 ,0 };
//%终端位置 rpy xyz
float q_term_ref[6] = { 1 * pi * 0 ,-22 / 57.3 * 0 , pi * 0 ,1.06 + 1e-5, 0,0.8 };
float qd_term_ref[6] = { 0, 0, 0, 0, 0 ,0 };最终C++下整个优化接口如下:
int test_code() {
#if 0//Compile the c-code
printf("Compilation c code!!\n");
int flag = system("gcc -fPIC -shared -O1 nlp.c -o nlp.so");
casadi_assert(flag == 0, "Compilation failed");
#endif
Dict opts;
opts["expand"] = true;
opts["max_iter"] = 1500;
opts["acceptable_tol"] = 1e-4;
opts["acceptable_obj_change_tol"] = 1e-6;
opts["tol"] = 1e-4;
opts["nlp_scaling_method"] = "gradient-based";
opts["constr_viol_tol"] = 1e-3;
opts["fixed_variable_treatment"] = "relax_bounds";
Function solver = nlpsol("solver", "ipopt", "nlp.so");//建立求解器 读取编译库 不需要在增加opt
printf("NLP Loaded!\n");
// Bounds and initial guess
int Sect = 4;// % 相序数量
int N = 40;// % 总分段比例 多相序为增加MPC控制精度应该 计算出个阶段末端状态作为约束 分段进行MPC控制 必须是偶数
float T = 0.8;// % 总时间长度 可以改成按时间规划相序
float Fmax = 128;
float max_jump_z = 1.2;// %最高跳跃高度 但是不能保证一定跳跃到
float min_damp_z = 0.15; //%最低限制高度
float max_lift_spdz = 4.5;// %最大离地速度
float z_init = 0.15; //%起始站立高度
float world_mu = 0.75;// %摩擦系数
float world_g = 9.81;
float Body_m = Mw;
int n_equa_c = 1144;
int n_inequa_c = 1800;
//%初始状态 rpy xyz
float q_init_val[6] = { 0 ,0 ,0 ,0, 0, z_init };
float qd_init_val[6] = { 0, 0, 0, 0, 0 ,0 };
//%终端位置 rpy xyz
float q_term_ref[6] = { 1 * pi * 0 ,-22 / 57.3 * 0 , pi * 0 ,1.06 + 1e-5, 0,0.8 };
float qd_term_ref[6] = { 0, 0, 0, 0, 0 ,0 };
//运动相序
DM Td_f1 = DM::vertcat({ 1, 1, 1, 1 });
DM Phase1 = DM::repmat(Td_f1, 1, 15);
DM Td_f2 = DM::vertcat({ 1, 1, 1, 1 });
DM Phase2 = DM::repmat(Td_f2, 1, 5);
DM Td_f3 = DM::vertcat({ 0, 0, 0, 0 });
DM Phase3 = DM::repmat(Td_f3, 1, 19);
DM Td_f4 = DM::vertcat({ 0, 0, 0, 0 });
DM Phase4 = DM::repmat(Td_f4, 1, 1);
DM cs_val=DM::horzcat({ Phase1,Phase2,Phase3,Phase4}).T();
std::map<std::string, DM> arg, res;
DM lbg = DM(1, 2944);
DM ubg = DM(1, 2944);
for (int i = n_equa_c + 1 - 1; i < n_equa_c + n_inequa_c ; i++)
lbg(i) = -inf;
for (int i = n_equa_c + 1 - 1; i < n_equa_c + n_inequa_c; i++)
ubg(i) = 0;//不加无法优化
//%% 状态上边界
//tempub = [Body.m*world.g*world.mu * 6; Body.m*world.g*world.mu * 6; Fmax];
//args.ubx = [];
//UBx = [pi * 3 * ones(3, 1); 10 * ones(2, 1); 1; ...
// pi * 3 * ones(3, 1); 40 * ones(3, 1)]; %状态上届 约束跳的最高高度
//UBx(6) = max_jump_z;
//UBx(12) = max_lift_spdz;
//UBx = repmat(UBx, N + 1, 1);
//UBf = [tempub; tempub; tempub; tempub];
//UBf = repmat(UBf, N, 1);
//UBp = repmat([0.4; 0.4; inf], 4, 1);
//UBp = repmat(UBp, N, 1);
//args.ubx = [args.ubx; UBx; UBf; UBp];
vector<float> tempub = { Body_m*world_g*world_mu * 6, Body_m*world_g*world_mu * 6, Fmax };
DM UBxt = DM::vertcat({ pi*DM::ones(3, 1), 10 * DM::ones(2, 1) ,1,pi * 3 * DM::ones(3,1),40 * DM::ones(3, 1) });
UBxt(6 - 1) = max_jump_z;
UBxt(12 - 1) = max_lift_spdz;
DM UBx = DM::repmat(UBxt, N + 1, 1);
DM UBft = DM::vertcat({ tempub, tempub, tempub, tempub });
DM UBf = DM::repmat(UBft, N, 1);
DM tempubb = DM::vertcat({ 0.4, 0.4, inf });
DM UBpt = DM::repmat(tempubb, 4, 1);
DM UBp = DM::repmat(UBpt, N, 1);
//cout << UBp << endl;
DM ubx = DM::vertcat({ UBx, UBf, UBp });
//cout << "ubx: " << ubx << endl;
//%% 状态下边界
// templb = [-Body.m*world.g*world.mu * 6; -Body.m*world.g*world.mu * 6; 0]; %力状态
// args.lbx = [];
//LBx = [-pi * 3 * ones(3, 1); -10 * ones(2, 1); min_damp_z; ...
// - pi * 3 * ones(3, 1); -40 * ones(3, 1)]; %状态下界
// LBx = repmat(LBx, N + 1, 1);
//LBf = [templb; templb; templb; templb];
//LBf = repmat(LBf, N, 1);
//LBp = repmat([-0.4; -0.4; -inf], 4, 1);
//LBp = repmat(LBp, N, 1);
//args.lbx = [args.lbx; LBx; LBf; LBp];
vector<float> templb = { -Body_m * world_g*world_mu * 6, -Body_m * world_g*world_mu * 6, 0 };
DM LBxt = DM::vertcat({ -pi * 3 * DM::ones(3, 1), -10 * DM::ones(2, 1) ,min_damp_z, -pi * 3 * DM::ones(3,1),-40 * DM::ones(3, 1) });
DM LBx = DM::repmat(LBxt, N + 1, 1);
DM LBft = DM::vertcat({ templb, templb, templb, templb });
DM LBf = DM::repmat(LBft, N, 1);
DM templbb = DM::vertcat({ -0.4, -0.4, -inf });
DM LBpt = DM::repmat(templbb, 4, 1);
DM LBp = DM::repmat(LBpt, N, 1);
DM lbx = DM::vertcat({ LBx, LBf, LBp });
//M = diag(SX([3, 4, 5, 6]))
//DM t1 = DM::vertcat({ 0.2 ,0.1, -z_init });
//DM t2 = DM::repmat(t1, 1, 4);
DM c_ref = DM(12, 1);
c_ref(0) = 0.2; c_ref(1) = 0.1; c_ref(2) = -z_init;
c_ref(3) = 0.2; c_ref(4) = -0.1; c_ref(5) = -z_init;
c_ref(6) = -0.2; c_ref(7) = 0.1; c_ref(8) = -z_init;
c_ref(9) = -0.2; c_ref(10)= -0.1; c_ref(11)= -z_init;
DM f_ref = DM(12, 1);
//cout << f_ref << endl;
DM Xref_val = DM(12, N + 1);
for (int i = 0; i < 6; i++) {
float d_add = (q_term_ref[i] - q_init_val[i]) / (N + 1);
for (int j = 0; j < N + 1; j++) {
Xref_val(i, j) = q_init_val[i] + d_add * j;
//for (int i = 6; i < 12; i++) {
// float d_add = (qd_term_ref[i] - qd_init_val[i]) / (N + 1);
// for (int j = 0; j < N + 1; j++) {
// Xref_val(i, j) = qd_init_val[i] + d_add * j;
DM F_ref = DM(12, N);
//DM Uref_val = DM(24, N + 1);
//for (int leg = 0; leg < 4; leg++) {
// for (int xyz = 0; xyz < 3; xyz++) {
// Uref_val(3 * (leg - 1) + xyz, :) = Xref_val(xyz, 1:end - 1) + c_ref(3 * (leg - 1) + xyz);
// Uref_val(12 + 3 * (leg - 1) + xyz, :) = f_ref(xyz).*ones(1, N);
DM r_ref = c_ref;
for (int i = 0; i < N-1; i++)
r_ref= DM::horzcat({ r_ref,c_ref });
//cout << r_ref << endl;
//for i = 1:6
// Xref_val(i, :) = linspace(q_init_val(i), q_term_ref(i), N + 1);
// Xref_val(6 + i, :) = linspace(qd_init_val(i), qd_term_ref(i), N + 1);
//end
//args.p = [reshape(Xref_val, n_state*(N + 1), 1); reshape(F_ref, n_F*N, 1); reshape(r_ref, n_r*N, 1); reshape(cs_val',4*N,1)];%送入了轨迹约束 相序约束
//args.x0 = [reshape(Xref_val, n_state*(N + 1), 1); reshape(F_ref, n_F*N, 1); reshape(r_ref, n_r*N, 1)]; %系统初始状态
/*DM p_Xref_val= DM(12*(N+1), 1);
for (int i = 0; i < N ; i++) {
for (int j = 0; j < 12; j++) {
p_Xref_val(i*12+j, 1) = Xref_val(j, i);
DM p_Xref_val=DM::reshape(Xref_val, 12*(N + 1), 1);
DM p_F_ref = DM::reshape(F_ref, 12*N, 1);
DM p_r_ref = DM::reshape(r_ref, 12*N, 1);
DM p_cs_val = DM::reshape(cs_val.T(),4*N,1);
DM p= DM::vertcat({ p_Xref_val,p_F_ref,p_r_ref,p_cs_val });
DM x0 = DM::vertcat({ p_Xref_val,p_F_ref,p_r_ref });
arg["lbx"] = lbx;
arg["ubx"] = ubx;
arg["lbg"] = lbg;
arg["ubg"] = ubg;
arg["x0"] = x0;
arg["p"] = p;
// Solve the NLP
res = solver(arg);//送入优化器
vector<float> w_opt(res.at("x"));//读取优化结果
float x_li_all[12][40];//系统状态轨迹输出
for (int i = 0; i <40; i++) {
for (int j = 0; j < 12; j++) {
x_li_all[j][i] = w_opt[i*12+j];
//printf("pos[%d] Pos:%f %f | Spd=%f %f\n", i, x_li_all[3][i], x_li_all[5][i], x_li_all[9][i], x_li_all[11][i]);
float f_lit[12][40];//力输出
for (int i = 0; i < 40; i++) {
for (int j = 0; j < 12; j++) {
f_lit[j][i] = w_opt[i * 12 + j+ 12 * (N + 1) + 1 - 1];
//printf("ff[%d] x=%f %f z=%f %f \n", i, f_lit[0][i], f_lit[3][i], f_lit[2][i], f_lit[5][i]);
//轨迹转换输出
motion_p.sect_dt = T / N;
motion_p.act_sect = N - 1;
for (int i = 0; i < N; i++)
motion_p.Att_n[i].x = x_li_all[0][i];
motion_p.Att_n[i].y = x_li_all[1][i];
motion_p.Att_n[i].z = x_li_all[2][i];
motion_p.Cog_n[i].x = x_li_all[3][i];
motion_p.Cog_n[i].y = x_li_all[4][i];
motion_p.Cog_n[i].z = x_li_all[5][i];
motion_p.DAtt_n[i].x = x_li_all[6][i];
motion_p.DAtt_n[i].y = x_li_all[7][i];
motion_p.DAtt_n[i].z = x_li_all[8][i];
motion_p.DCog_n[i].x = x_li_all[9][i];
motion_p.DCog_n[i].y = x_li_all[10][i];
motion_p.DCog_n[i].z = x_li_all[11][i];
printf("[%d][%d] Pos: %f %f | Spd: %f %f \n", i,
motion_p.mpc_table[0][i],
motion_p.Cog_n[i].x,
motion_p.Cog_n[i].z,
motion_p.DCog_n[i].x,
motion_p.DCog_n[i].z);
/*printf("[%d][%d] Att: %f %f | Rate: %f %f \n", i,
motion_p.mpc_table[0][i],
motion_p.Att_n[i].y,
motion_p.Att_n[i].z,
motion_p.DAtt_n[i].y,
motion_p.DAtt_n[i].z);*/
for (int i = 0; i < N; i++)
motion_p.Ff_n[2][i].x = f_lit[0][i];
motion_p.Ff_n[2][i].y = f_lit[1][i];
motion_p.Ff_n[2][i].z = f_lit[2][i];
if (motion_p.Ff_n[2][i].z > 0.0001)
motion_p.mpc_table[2][i] = 1;
motion_p.mpc_table[2][i] = 0;
motion_p.Ff_n[0][i].x = f_lit[3][i];
motion_p.Ff_n[0][i].y = f_lit[4][i];
motion_p.Ff_n[0][i].z = f_lit[5][i];
if (motion_p.Ff_n[0][i].z > 0.000001)
motion_p.mpc_table[0][i] = 1;
motion_p.mpc_table[0][i] = 0;
motion_p.Ff_n[3][i].x = f_lit[6][i];
motion_p.Ff_n[3][i].y = f_lit[7][i];
motion_p.Ff_n[3][i].z = f_lit[8][i];
if (motion_p.Ff_n[3][i].z > 0.00001)
motion_p.mpc_table[3][i] = 1;
motion_p.mpc_table[3][i] = 0;
motion_p.Ff_n[1][i].x = f_lit[9][i];
motion_p.Ff_n[1][i].y = f_lit[10][i];
motion_p.Ff_n[1][i].z = f_lit[11][i];
if (motion_p.Ff_n[1][i].z > 0.00001)
motion_p.mpc_table[1][i] = 1;
motion_p.mpc_table[1][i] = 0;
printf("[%d] F[%d]:%f %f | [%d]:%f %f \n", i,
motion_p.mpc_table[0][i], motion_p.Ff_n[0][i].x, motion_p.Ff_n[0][i].z,
motion_p.mpc_table[2][i], motion_p.Ff_n[2][i].x, motion_p.Ff_n[2][i].z);
printf("[%d] H[%d]:%f %f | [%d]:%f %f \n", i,

