【R语言】多元线性回归实践——什么最影响你的幸福指数

本文通过一个案例把R语言回归分析中常用的知识点串起来，欢迎关注交流学习（添加微信公众号： 素言素语Sue )

从Kaggle上获得了2019年全球156个国家幸福指数数据集（World Happiness Report，数据源： https://www. kaggle.com/PromptCloudH Q/world-happiness-report-2019 ）

各数据列分别为：

l Overall rank （整体排名）

l Country or region（国家或地区）

l Score（幸福值得分）

l GDP per capita（人均GDP）

l Social support（社会支持）

l Healthy life expectancy（健康寿命预期）

l Freedom to make life choices（自由选择的程度）

l Generosity（慷慨度）

l Perceptions of corruption（对腐败的认知度）

Score值越大，意味着幸福指数越高。我们想通过多元线性回归模型来看，幸福指数受到哪些指标的影响以及影响程度大小。

接下来内容主要包括四个方面：

1. 数据预处理

2. 建立模型-模型诊断-调整改进

3. 模型解释

4. 模型预测及效果评估

1.数据预处理

打开数据文件，查看数据集基本情况，本数据集共156条，9列数据，大部分为number类型。

data_raw<-read.csv(file.choose())
str(data_raw)
##输出结果：
'data.frame':  156 obs. of  9 variables:
 $ Overall.rank                : int  1 2 3 4 5 6 7 8 9 10 ...
 $ Country.or.region           : Factor w/ 156 levels "Afghanistan",..: 44 37 106 58 99 134 133 100 24 7 ...
 $ Score                       : num  7.77 7.6 7.55 7.49 7.49 ...
 $ GDP.per.capita              : num  1.34 1.38 1.49 1.38 1.4 ...
 $ Social.support              : num  1.59 1.57 1.58 1.62 1.52 ...
 $ Healthy.life.expectancy     : num  0.986 0.996 1.028 1.026 0.999 ...
 $ Freedom.to.make.life.choices: num  0.596 0.592 0.603 0.591 0.557 0.572 0.574 0.585 0.584 0.532 ...
 $ Generosity                  : num  0.153 0.252 0.271 0.354 0.322 0.263 0.267 0.33 0.285 0.244 ...
 $ Perceptions.of.corruption   : num  0.393 0.41 0.341 0.118 0.298 0.343 0.373 0.38 0.308 0.226 ...

源数据集各列的列名太长了，先重新定义一下列名，方便后续使用。

colnames(data_raw)<-c("Rank","Country","Score","GDP.per","Social.support","Lift.expect","Freedom","Generosity","Perception")

查看缺失值，这个数据集比较规范和完整，各列没有缺失值。（如果有缺失值的话，需要根据情况填充或删除。一种典型的填充方法是用现有的平均值，中位数或模式代替缺失值）

sapply(data_raw, function(x) sum(is.na(x)))

选取需要的数据子集，这里我们只需要看幸福指数Score及其6个潜在影响因素。

data<-data_raw[3:9]

接下来看看这些变量之间的相关情况及变量自身的分布情况，可使用方阵散点图（scatterplotMatrix）。在此之前，需要加载car包。

需要说明一下，正常情况下通过install.packages("car") 语句加载即可，不过我在加载时出现了加载失败的情况，因此直接通过填入car包url链接地址的方式加载。

p_url<-"https://cran.r-project.org/bin/windows/contrib/4.1/carData_3.0-3.zip"
install.packages(p_url,repos=NULL,type="source")
library(car) 
scatterplotMatrix(data,smoother=F) 

因为变量较多，图看起来不太友好……不过大致可以看出Score近似正态分布，不过出现了双峰，可以用powerTransform来检验是否需要正态转换。

另外从第一行基本可以看出，前4个潜在影响因素与Score存在比较明显的线性关系，后两个变量不太明显。

下面是对因变量Y（Score）正态变换的检验，结果显示可以用Score的0.9 (0.8865)次方变换，但是 λ=1 的P值无法拒绝原假，因此无需转换。

summary(powerTransform(data$Score))
#输出结果
bcPower Transformation to Normality 
           Est Power Rounded Pwr Wald Lwr Bnd
data$Score    0.8865           1       0.2008
……（这里省略了部分输出结果）……
Likelihood ratio test that no transformation is needed
                            LRT df    pval
LR test, lambda = (1) 0.1047618  1 0.74619

上面的方阵散点图看着比较费劲，我们换个友好的图，看看各变量的相关性矩阵。从图来看，前三个变量与Ｓｃｏｒｅ有较强的相关性，其余的有２个相关性一般，１个相关性较弱。

url_c<-"https://cran.r-project.org/bin/windows/contrib/4.1/corrplot_0.84.zip"
install.packages(url_c,repos=NULL,type="source")
library(corrplot)
datacor<-cor(data)
corrplot(datacor,method="number")

ok，从以上的预处理和基本分析中，大致了解了数据集的基本情况及变量之间的关系。

2.建立模型-模型诊断-调整改进

• 2.1 建立模型

我们要建立多元线性回归模型并评估模型的预测能力，需要先将数据随机分为训练组和测试组，二者数据规模比例设置为8：2.

packageurl<-"https://cran.r-project.org/bin/windows/contrib/4.1/caTools_1.18.0.zip"
install.packages(packageurl,repos=NULL,type="source")
library(caTools)
set.seed(001)
split<-sample.split(data$Score,SplitRatio=0.8) 
train_data<-subset(data,split==TRUE) 
test_data<-subset(data,split==FALSE)

接下来进行多元线性回归（Multiple Linear Regression）模型拟合。从拟合结果来看，前四个变量系数显著（P<0.01,P<0.001），最后两个变量系数不显著，调整后的R2 为76.49%。

fit<-lm(Score~.,data = train_data)
summary(fit)
#输出结果：
Call:
lm(formula = Score ~ ., data = train_data)
Residuals:
     Min       1Q   Median       3Q      Max 
-1.65732 -0.36090  0.06218  0.37079  1.19342 
Coefficients:
               Estimate Std. Error t value Pr(>|t|)    
(Intercept)      1.7436     0.2430   7.175 7.13e-11 ***
GDP.per          0.7057     0.2672   2.641  0.00940 ** 
Social.support   1.0635     0.2635   4.036 9.75e-05 ***
Lift.expect      1.2957     0.4205   3.081  0.00257 ** 
Freedom          1.4045     0.4265   3.293  0.00131 ** 
Generosity       0.6890     0.5745   1.199  0.23288    
Perception       0.9598     0.6363   1.508  0.13415    
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.5453 on 117 degrees of freedom
Multiple R-squared:  0.7764,	Adjusted R-squared:  0.7649 
F-statistic:  67.7 on 6 and 117 DF,  p-value: < 2.2e-16

• 2.2 模型诊断

一个好的多元线性回归模型应当尽量满足4点假设前提，可用plot绘制残差分析四张图进行初步检验。

p<-par(mfrow=c(2,2))
plot(fit) 

1. 因变量与自变量存在线性关系（左上图对应此检验）满足假设的情况是：若因变量与自变量线性相关，那么残差值与预测（拟合）值就没有任何系统关联（即预测值周围的点均匀分布）。
2. 残差呈正态分布（右上图对应此检验） 满足假设的情况是：当预测变量值固定时，因变量成正态分布，则残差值也应该是一个均值为0的正态分布。
3. 残差满足方差齐性，即同方差（左下图对应此检验）满足假设的情况是： 排除残差与自变量还有关系，即水平线周围的点应该随机分布。
4. 无明显异常值（右下图对应此检验：残差—杠杆图的可读性差而且不够实用。可采用其他方法）

从残差分析的四图结果来看，有几个异常值比较明显，其他表现尚可。

在《R语言实践》中还提供了一种方法，可使用gvlma包的gvlma()函数对拟合模型的假设作 综合验证 ，并对峰度、偏度进行验证。

运行结果中的Global Stat是对4个假设条件进行综合验证，通过了即表示4个假设验证都通过了。 注意这里假设检验的原假设都是假设成立，所以当p>0.05时，假设才能能过验证。很显然，这个模型的Global Stat综合验证并未通过。

install.packages("gvlma")
library(gvlma)
gvlma(fit)
#输出结果
Call:
 gvlma(x = fit) 
                    Value   p-value                   Decision
Global Stat        33.848 8.006e-07 Assumptions NOT satisfied!
Skewness            5.777 1.624e-02 Assumptions NOT satisfied!
Kurtosis            1.614 2.039e-01    Assumptions acceptable.
Link Function      16.842 4.062e-05 Assumptions NOT satisfied!
Heteroscedasticity  9.615 1.930e-03 Assumptions NOT satisfied!

前面我们观察到了存在比较明显的异常值，初步猜测对模型有较大的影响。我们 也可以一个个看看这些假设条件，对每一个使用单独的检测方法进行检测 。（限于篇幅这里略过，感兴趣的可以查看公众号同名文章里的详细解释，公众号： 素言素语Sue ）

这里直接对异常值进行单独检测。

异常值有以下观测指标——

• 远离回归线的离群点：学生化残差rstudent；
• 远离自变量均值的杠杆点：杠杆值hatvalues；
• 对回归线有重要影响的影响点：考科斯距离cooks.distance。

car包中influencePlot函数能将三个指标用气泡图形式将它们绘制出来。

每一个观测方式都有自己的取舍规则，这里不一一展开。我们参考一个粗糙的判断准则：标准化残差值大于2或者小于-2的点可能是离群点，以此作为异常值判断依据。从图结果来看，三个比较明显的异常值为：152,131,148。

influencePlot(fit,id=list(method="identify"),main="influence plot")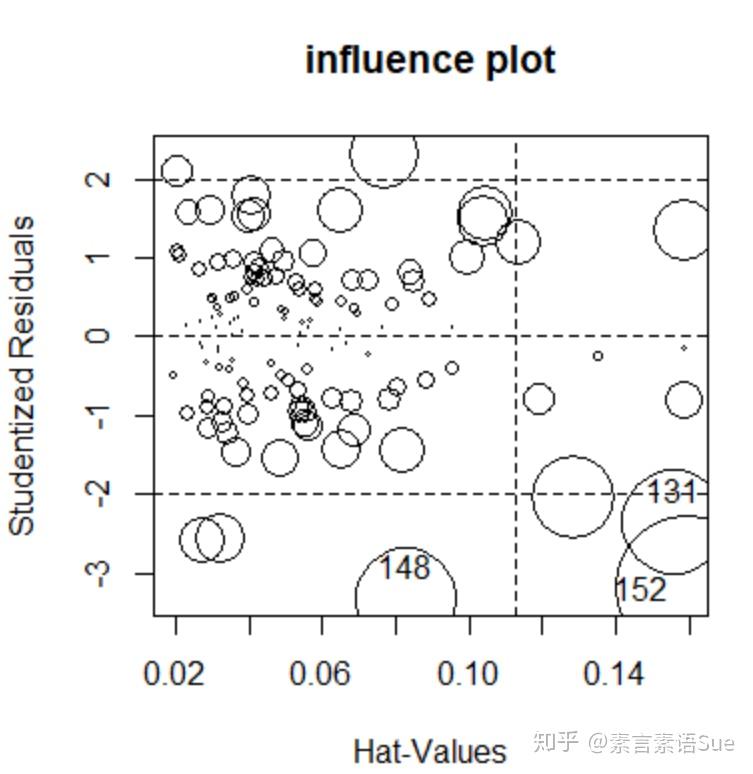

其他的检验：

Ø 误差独立性检验，若P不显著，说明误差之间独立。本结果p=0.034<0.05,但DW= 1.629046在1.4~2.6的范围内，说明自相关并不明显

durbinWatsonTest(fit)

Ø 多重共线性检验，结果都在0~5以内（一般0-10以内都可容忍），说明多重共线性不严重。

vif(fit) 

• 2 .3 模型改进1：异常值处理

通过查看源数据发现，删除这三个异常值（131，148，152）对总体数据和分析解释上没有太大影响，因此尝试删除这三个异常值，重新进行模型拟合。

data_f<-data[-152,]
data_f<-data_f[-148,]
data_f<-data_f[-131,]

随后，再次随机分出训练数据集和验证数据集，并使用训练数据集拟合模型。从结果来看，Generosity系数仍不显著，Perception系数变为了显著，调整后的R2 从原来的76.49%变为了82.29%，改进的效果比较明显。

library(caTools)
set.seed(001)
split<-sample.split(data_f$Score,SplitRatio=0.8)
train_data_f<-subset(data_f,split==TRUE) 
test_data_f<-subset(data_f,split==FALSE)
fit_1<-lm(Score~.,data = train_data_f)
summary(fit_1)
#输出结果：
Call:
lm(formula = Score ~ ., data = train_data_f)
Residuals:
    Min      1Q  Median      3Q     Max 
-1.3862 -0.3255  0.0601  0.3004  0.9942 
Coefficients:
               Estimate Std. Error t value Pr(>|t|)    
(Intercept)      1.8859     0.2050   9.198 1.92e-15 ***
GDP.per          0.7727     0.2253   3.429 0.000842 ***
Social.support   0.8958     0.2259   3.965 0.000128 ***
Lift.expect      1.0758     0.3239   3.322 0.001200 ** 
Freedom          1.7760     0.3686   4.818 4.47e-06 ***
Generosity       0.8336     0.5305   1.571 0.118841    
Perception       1.4424     0.5652   2.552 0.012017 *  
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.4667 on 115 degrees of freedom
Multiple R-squared:  0.8317,	Adjusted R-squared:  0.8229 
F-statistic: 94.71 on 6 and 115 DF,  p-value: < 2.2e-16

接下来的操作类似，对改进后的模型fit_1进行残差诊断（四个图），并对拟合模型的假设作综合验证。从四图结果来看，仍有一些“异常值”，其他表现尚可，但综合验证结果已经通过，不再进一步删减这些“异常值”。

p<-par(mfrow=c(2,2))
plot(fit_1) 
gvlma(fit_1)
#输出结果：
Call:
 gvlma(x = fit_1) 
                      Value p-value                   Decision
Global Stat        6.907351 0.14087    Assumptions acceptable.
Skewness           1.568658 0.21040    Assumptions acceptable.
Kurtosis           0.000253 0.98731    Assumptions acceptable.
Link Function      4.133001 0.04205 Assumptions NOT satisfied!
Heteroscedasticity 1.205438 0.27224    Assumptions acceptable.

• 2.4 模型改进2：不显著的变量

去掉系数不显著的变量Generosity，重新拟合得到模型fit_2，从结果来看，各变量系数均显著（P<0.05），调整后的R2 为82.07%，解释度较高。

残差分析plot(fit_2)与综合验证gvlma(fit_2) 过程与上文相同，不再赘述。综合验证结果通过，残差分析也较符合条件。

fit_2<-update(fit_1,.~.-Generosity)
summary(fit_2)
#输出结果：
Call:
lm(formula = Score ~ GDP.per + Social.support + Lift.expect + 
    Freedom + Perception, data = train_data_f)
Residuals:
     Min       1Q   Median       3Q      Max 
-1.31809 -0.33352  0.05878  0.30877  1.02630 
Coefficients:
               Estimate Std. Error t value Pr(>|t|)    
(Intercept)      2.0207     0.1874  10.783  < 2e-16 ***
GDP.per          0.7201     0.2242   3.211 0.001711 ** 
Social.support   0.8877     0.2273   3.905 0.000159 ***
Lift.expect      1.0948     0.3257   3.361 0.001051 ** 
Freedom          1.8427     0.3685   5.001 2.05e-06 ***
Perception       1.7304     0.5380   3.216 0.001684 ** 
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.4697 on 116 degrees of freedom
Multiple R-squared:  0.8281,	Adjusted R-squared:  0.8207 
F-statistic: 111.7 on 5 and 116 DF,  p-value: < 2.2e-16

3.模型解释

从以上最终得到的模型（fit_2）可表示为：

YScore =2.02+0.72*GDP.per+0.89*Social.support+1.09*Lift.expect+1.84*Freedom+1.73*Perception

即GDP.per得分每提高一个单位，幸福指数提升0.72个单位；Freedom每提高1单位，幸福指数则提高1.84单位。

可见，拥有自由选择的能力更容易令人感到幸福啊，甚至比提升经济还有效！

4. 模型预测效果评估

使用模型处理测试组数据(test_data)，得到Score的预测结果fit_pre，并与训练集的实际结果对比，以评估模型预测效果。具体为：

将预测结果和实际结果放到同一个坐标系里，分别作为横轴和纵轴绘制散点图，并添加斜线。从图结果来看，预测值与实际值比较均匀的分布在45°线的两侧。说明模型预测效果良好，有一定的参考价值。

fit_pre<-predict(fit_2,newdata = test_data)
pre_actual<-as.data.frame(cbind(Prediction=fit_pre,Actual=test_data$Score))
library(ggplot2)
line<-ggplot(pre_actual,aes(Actual,Prediction))+geom_point()+theme_bw()+geom_abline()+labs(title = "Multiple Linear Regression Predict vs Actual",x="Actual",y="Prediction")
line

【附】完整的R脚本：

#数据预处理
data_raw<-read.csv(file.choose())
str(data_raw)
colnames(data_raw)<-c("Rank","Country","Score","GDP.per","Social.support","Lift.expect","Freedom","Generosity","Perception")
 data<-data_raw[3:9]
 #方阵散点图
p_url<-"https://cran.r-project.org/bin/windows/contrib/4.1/carData_3.0-3.zip"
install.packages(p_url,repos=NULL,type="source")
library(car) 
scatterplotMatrix(data,smoother=F) 
 #检验Y是否需要正态转换
summary(powerTransform(data$Score))
 #相关性矩阵
url_c<-"https://cran.r-project.org/bin/windows/contrib/4.1/corrplot_0.84.zip"
install.packages(url_c,repos=NULL,type="source")
library(corrplot)
datacor<-cor(data)
corrplot(datacor,method="number")
#训练集和测试集
packageurl<-"https://cran.r-project.org/bin/windows/contrib/4.1/caTools_1.18.0.zip"
install.packages(packageurl,repos=NULL,type="source")
library(caTools)
set.seed(001)
split<-sample.split(data$Score,SplitRatio=0.8) 
train_data<-subset(data,split==TRUE) 
test_data<-subset(data,split==FALSE)
#模型拟合
fit<-lm(Score~.,data = train_data)
summary(fit)
#回归诊断
p<-par(mfrow=c(2,2))
plot(fit) 
install.packages("gvlma")
library(gvlma)
gvlma(fit)
 #异常值检验
influencePlot(fit,id=list(method="identify"),main="influence plot")
 #其他检验
durbinWatsonTest(fit)
vif(fit)
#删除异常值
data_f<-data[-152,]
data_f<-data_f[-148,]
data_f<-data_f[-131,]
#重新拟合
library(caTools)
set.seed(001)
split<-sample.split(data_f$Score,SplitRatio=0.8)
train_data_f<-subset(data_f,split==TRUE) 
test_data_f<-subset(data_f,split==FALSE)
fit_1<-lm(Score~.,data = train_data_f)
summary(fit_1)
#回归诊断
p<-par(mfrow=c(2,2))
plot(fit_1) 
gvlma(fit_1)
#再次拟合
fit_2<-update(fit_1,.~.-Generosity)
summary(fit_2)