聚类分析(K-Means)

操作视频

# 1、作用

聚类分析(K-Means)是一种基于中心的无监督学习聚类算法（K 均值聚类），通过迭代，将样本分组成k个簇，使得每个样本与其所属类的中心或均值的距离之和最小。与分层聚类等按照字段进行聚类的算法不同的是，K-Means算法是按照样本进行聚类。

聚类分析的重要性主要体现在以下几个方面：首先，它可以帮助我们理解数据的分布和特征，发现潜在的数据模式；其次，通过聚类，我们可以识别出数据中的异常值或噪声，提高数据质量；最后，聚类分析还可以为后续的监督学习提供有价值的先验知识，如通过聚类结果初始化分类器的参数等。

在机器学习的广泛应用中，聚类分析发挥着不可或缺的作用。例如，在图像处理中，聚类可以用于图像分割、颜色量化等任务；在市场分析中，聚类可以帮助企业实现客户细分，制定更精准的营销策略；在生物信息学中，聚类则可用于基因表达数据的分析，揭示基因之间的相互作用关系。它可以应用于任何表格数据集，用于确定哪些行相似，并从数据集中形成有意义的群组。

# 2、输入输出描述

输入：1 个或1个以上的定类变量（独热编码非必选）或者定量变量，预先设定类别个数。
输出：根据预先设定的类别个数，划分为其设定的类别。

# 3、案例示例

根据调研用户的收入、年龄、学历等变量进行聚类。

# 4、案例数据

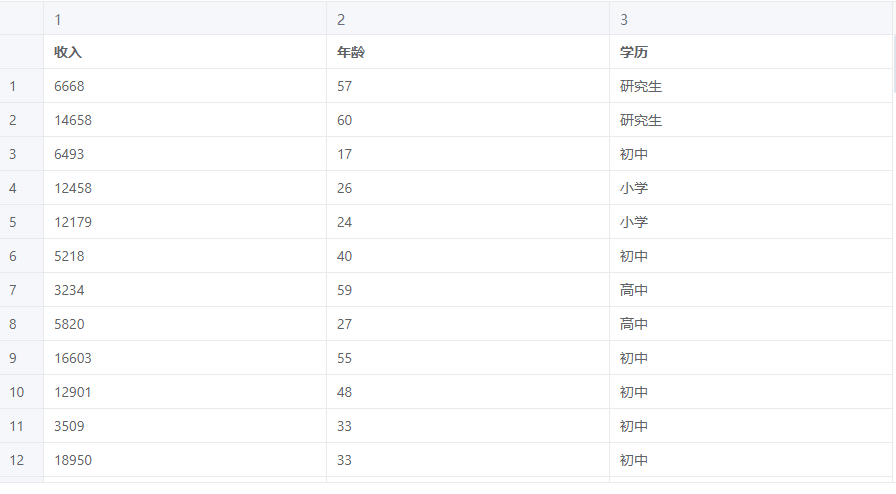
聚类分析案例数据

# 5、案例操作

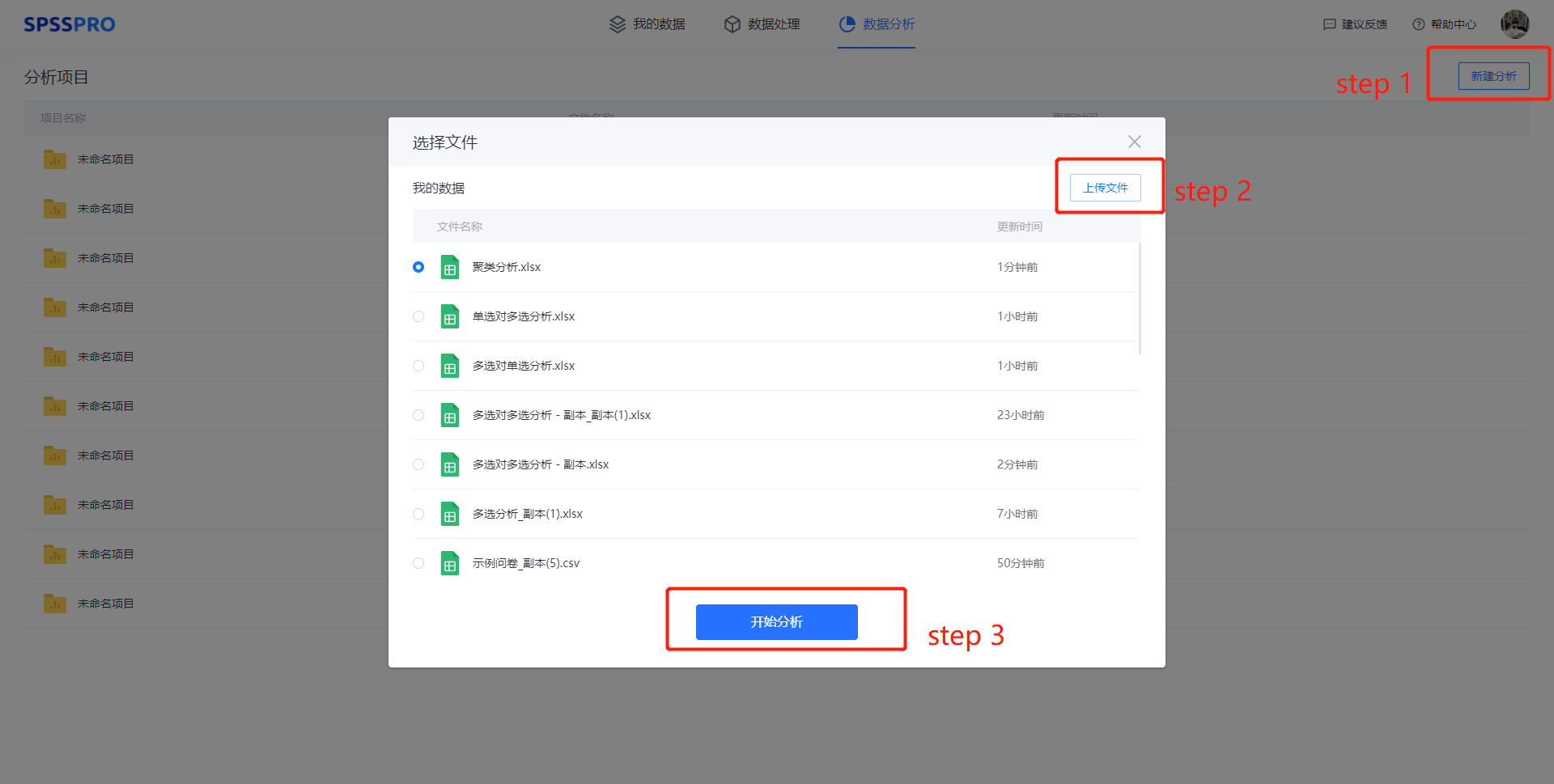
Step1：新建分析；
Step2：上传数据；
Step3：选择对应数据打开后进行预览，确认无误后点击开始分析；

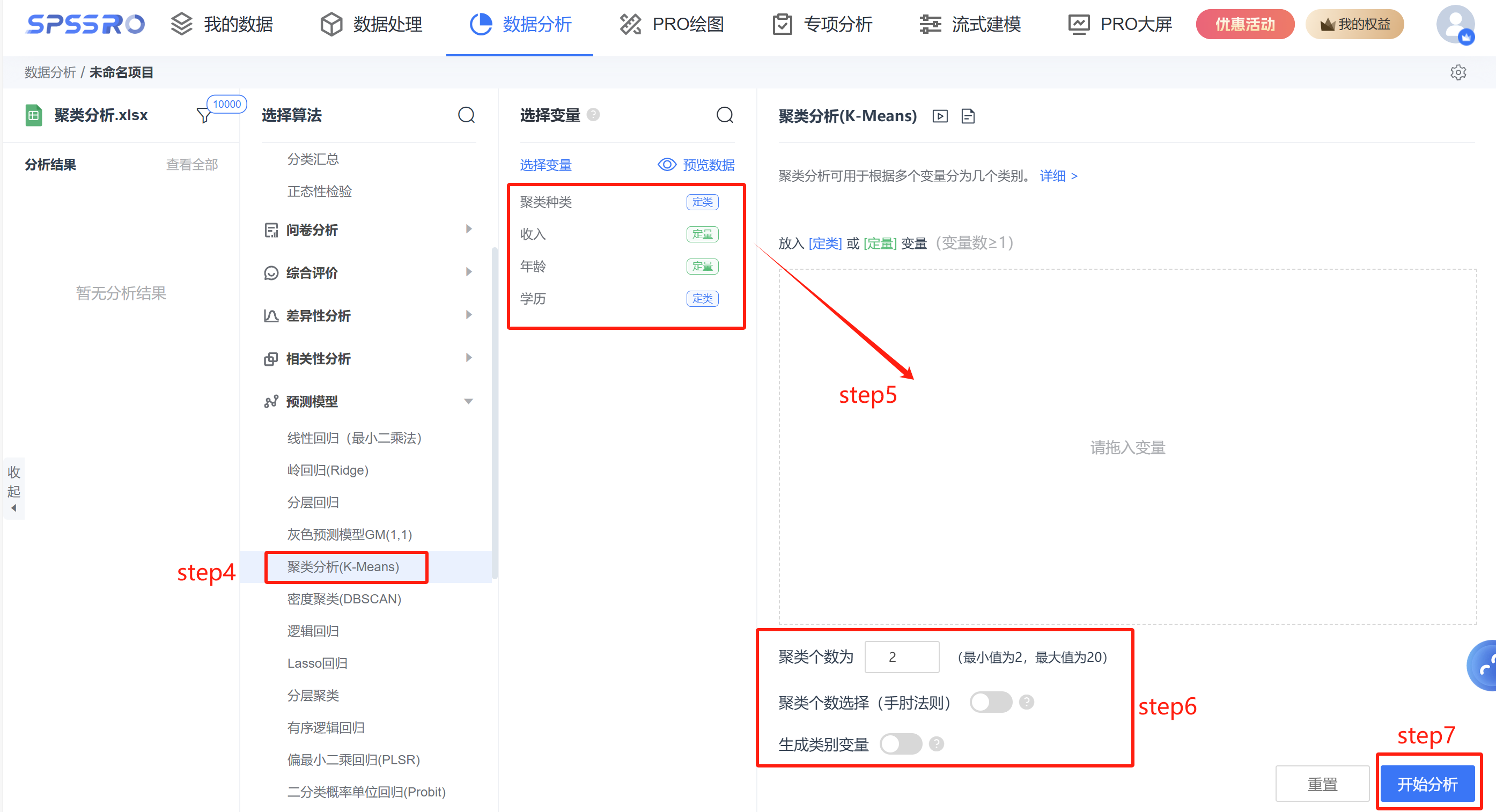
step4：选择【聚类分析（K-Means）】；
step5：查看对应的数据数据格式，按要求输入【聚类分析（K-Means）】数据；
step6：选择【聚类个数】等；
step7：点击【开始分析】，完成全部操作。

# 6、输出结果分析

输出结果 1：字段差异性分析 

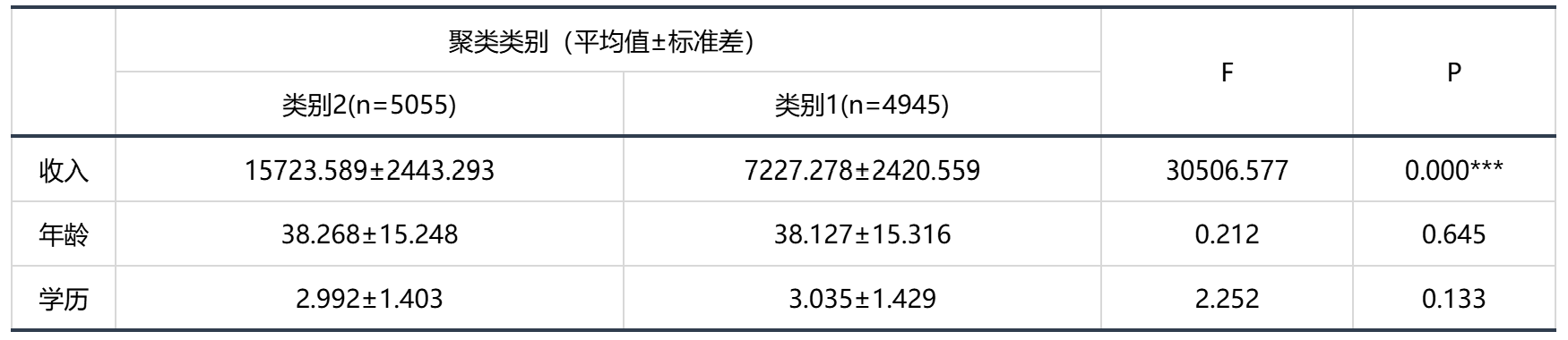
图表说明 ：上表展示了定量字段差异性分析的结果，包括平均值 ± 标准差的结果、F 检验结果、显著性 P 值。
分析：当设置聚类个数 K 值设置为 2 时，通过聚类分析，划分为了 2 个类别，方差分析的结果显示:
对于变量收入，两个类别的平均值 ± 标准差的显著性 P 值为 0.000，水平上呈现显著性，拒绝原假设，说明变量收入在聚类分析划分的类别之间存在显著性差异，分类有效；
对于变量年龄，显著性 P 值为 0.645，水平上不呈现显著性，不能拒绝原假设，说明变量年龄在聚类分析划分的类别之间不存在显著性差异，分类无效；
对于变量学历，显著性 P 值为 0.133，水平上不呈现显著性，不能拒绝原假设，说明变量学历在聚类分析划分的类别之间不存在显著性差异，分类无效；
综上所述，实际上设置为 2 个类别时，分类效果并非那么好，我们可以通过调整聚类个数进行重复验证。

输出结果 2：聚类汇总

图表说明 ：上表展示了模型聚类的结果，包括频数，所占百分比。
分析：聚类分析的结果显示，聚类结果共分为2类，聚类类别_1的频数为4945，所占百分比为49.45%；聚类类别_2的频数为5055，所占百分比为50.55%

输出结果 3：聚类汇总图

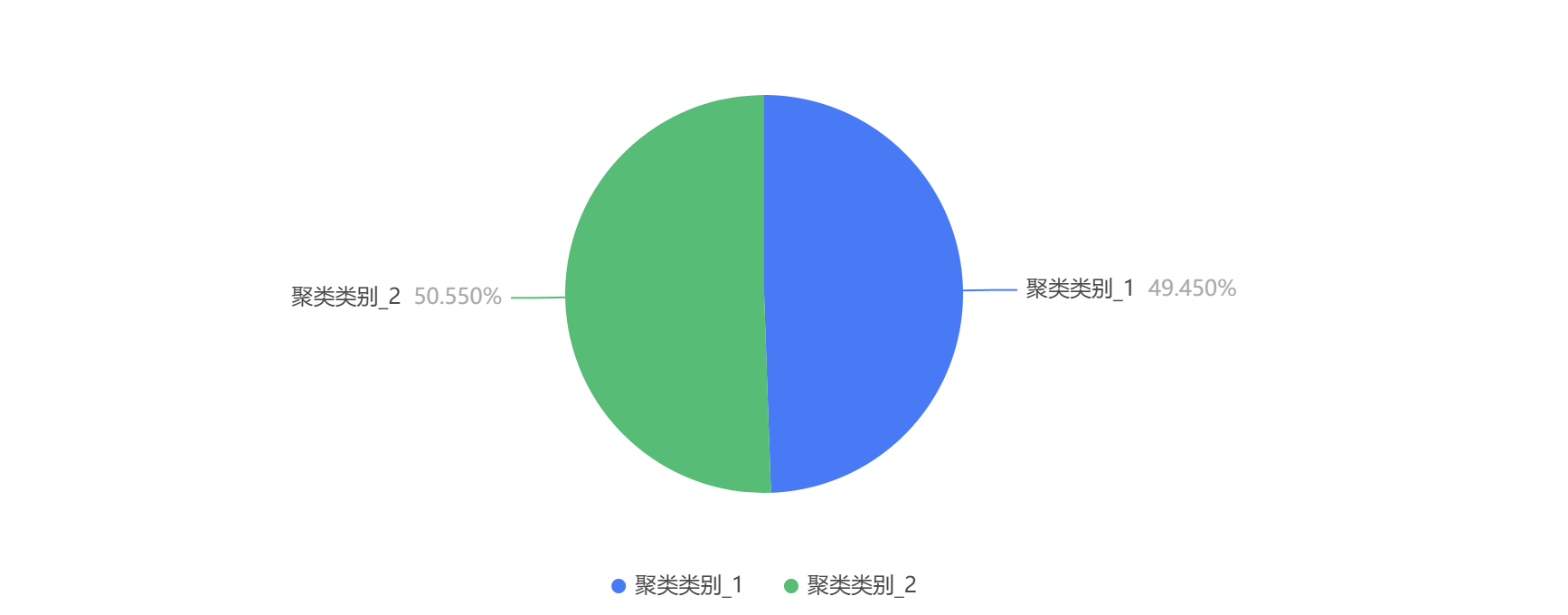
图表说明 ：上图以可视化的形式展示了模型聚类的结果，包括频数，所占百分比。可见两个类别大致五五开，数量差异很小。

输出结果 4：数据集聚类标注

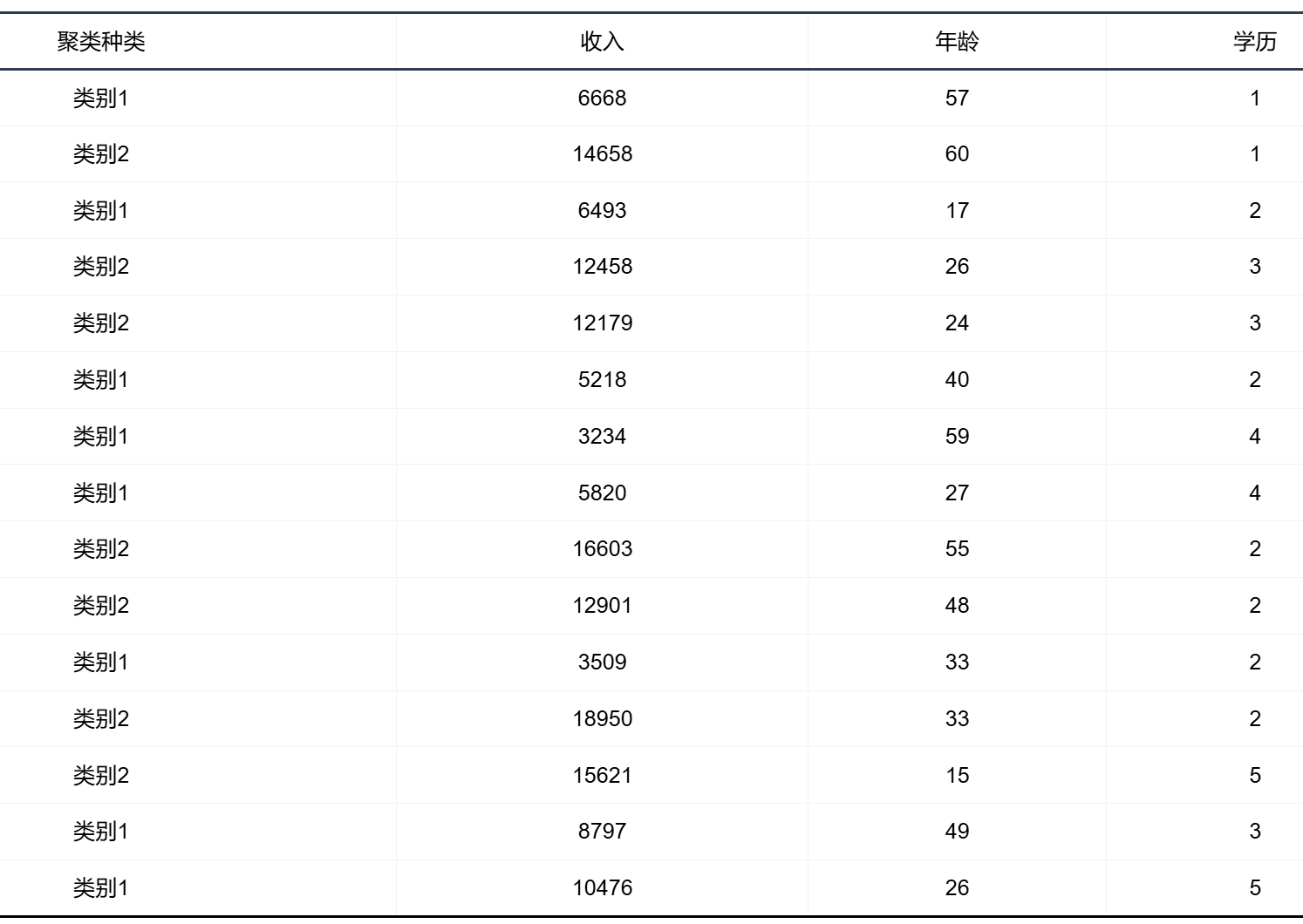
图表说明 ：上表格展示了模型聚类结果的部分数据聚类标注，其为预览结果，只显示综合排序的前15条数。

输出结果 5：聚类中心点坐标

图表说明 ：上表展示了部分模型聚类中心的数据。

输出结果6：聚类散点图

图表说明 ：若变量数等于两个，上图是根据两变量的数据绘制出来的散点图；若变量数大于两个，上图是提取主成分分析(PCA)降维后前两个主成分来绘制散点图，在一定程度上可查看聚类效果（若是前两个主成分的方差解释率较低，该图的意义不大）。
● 聚类散点图最大仅显示1000个样本量信息，若样本量大于1000，则在全样本中进行随机抽样，选取其中1000样本来进行散点图展示。

输出结果7：评价指标

图表说明 ：
● 轮廓系数：对于一个样本集合，它的轮廓系数是所有样本轮廓系数的平均值。轮廓系数的取值范围是[-1,1]，同类别样本距离越相近不同类别样本距离越远，分数越高，聚类效果越好。
● DBI（Davies-bouldin)：该指标用来衡量任意两个簇的簇内距离之后与簇间距离之比。该指标越小表示聚类效果越好。
● CH(Calinski-Harbasz Score)：通过计算类内各点与类中心的距离平方和来度量类内的紧密度（分母），通过计算类间中心点与数据集中心点距离平方和来度量数据集的分离度（分子），CH指标由分离度与紧密度的比值得到，CH越大表示聚类效果越好。

# 7、注意事项

K 均值聚类分析的 K 值需要先前指定,SPSSPRO 默认为 K=2。可以根据先验情况，或者使用手肘法（Elbow method）、轮廓系数法确定 K 值。在SPSSPRO中可使用手肘法则选择K值。
K 均值聚类分析（K-means）区分于 K 近邻（KNN),后者是一种监督学习的分类算法。
K 均值聚类分析（K-means）每次选取的随机聚类中心不一样，故带有随机性，每次结果不一定完全相同。
K-means算法在迭代过程中采用贪心策略，每一步都试图找到当前最优解。然而，这种策略可能导致算法陷入局部最优解，而无法达到全局最优。可以尝试使用不同的初始聚类中心进行多次运行。

# 8、模型理论

K-Means 算法 是一种无监督学习，同时也是基于划分的聚类算法，一般用欧式距离作为衡量数据对象间相似度的指标，相似度与数据对象间的距离成反比，相似度越大，距离越小。

算法需要预先指定初始聚类数目 k 以及 k 个初始聚类中心，根据数据对象与聚类中心之间的相似度，不断更新聚类中心的位置，不断降低类簇的误差平方和（Sum of Squared Error，SSE），当 SSE 不再变化或目标函数收敛时，聚类结束，得到最终结果。

其核心思想是 ：

初始化质心 ，即选取 $k$ 个初始聚类中心。可以根据先验知识选择，或根据样本初始的分布情况直观选择，或使用手肘图（elbow）等方法确定 $k$ 值。
分配簇 。通过计算每个数据点与质心的距离，并将其分配给距离最近的质心，为数据集中的每个点分配簇。

在k-means算法中，一般使用欧几里得距离（Euclidean distance）计算样本点到中心的距离：

d (x, c_{i}) = \sqrt{\sum_{j = 1}^{d} (x_{j} - c_{i j})^{2}}

其中， $x$ 为数据点， $C_{i}$ 为第 $i$ 个聚类中心， $d$ 为数据对象的维度， $x_{j}$ ， $C_{i j}$ 分别是 $x$ 和 $C_{i}$ 的第 $j$ 维上的值。

而K-Means的目标函数为：

J = m i n \sum_{i = 1}^{m} \sum_{k = 1}^{K} w_{i k} | | x_{i} - c_{k} | |^{2}

其中： $w_{i k}$ 为提示函数（indicator function）。如果数据点在簇内，则 $w_{i k} = 1$ ；反之， $w_{i k} = 0$ 。

而目标需要最小化 $J$ 来达到最优值，所以，我们需要分别对两个变量 $w_{i k}$ 和 $c_{k}$ 进行微分。在该步骤中，我们首先对 $w_{i k}$ 进行微分：

\frac{d J}{d w_{i k}} = \sum_{i = 1}^{m} \sum_{k = 1}^{K} | | x_{i} - c_{k} | |^{2}

通过计算，我们可以得到：如果 $k = a r g m i n | | x_{i} - c_{k} | |^{2}$ ,则结果为1；否则，结果为0。

也就是说，在这一步中， 数据点 $x_{i}$ 根据欧几里得距离被分配到最接近的质心 $c_{i}$ 。

更新质心 。重新计算每个簇的质心，即取簇内所有数据点的平均值作为新的质心。

在数据点被分配到某一个簇后，我们需要重新计算，找到最佳的质心。在一步中，我们对步骤二的目标函数的 $c_{k}$ 进行微分：

\frac{d J}{d c_{k}} = 2 * \sum_{k = 1}^{K} w_{i k} | | x_{i} - c_{k} | |^{2}

运算后可以得到:

c_{k} = \frac{\sum_{i}^{m} w_{i k} x_{i}}{\sum_{i}^{m} w_{i k}}

这个公式表明，新的簇质心 $c_{k}$ ,是该簇内所有数据点 $x_{i}$ 的加权平均值，权重是 $w_{i k}$ 。换句话说，它是簇 $𝑘$ 中所有数据点的中心点，是一个平均化的表示，这确保了在更新过程中质心会朝着簇内数据点的中心移动。

重复上述步骤，直到 聚类中心不再变化 或 达到最大的迭代次数 后停止。

# 9、参考文献

[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.
[2] Saroj，Kavita.Review：study on simple k mean and modified K mean clustering technique[J].International Journal of Computer Science Engineering and Technology，2016， 6（7）：279-281.
[3] 杨俊闯,赵超.K-Means 聚类算法研究综述[J].计算机工程与应用,2019,55(23):7-14+63.
[4] Wong J A H A .Algorithm AS 136: A K-Means Clustering Algorithm[J].Journal of the Royal Statistical Society, 1979, 28(1):100-108.DOI:10.2307/2346830.