var numbers = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
function oddCounter(numbers) {
var count = 0
numbers.forEach(number => {
if (isOdd(number)) {
count += 1
return count
oddCounter(numbers) // 5
// 工具函数,判断传入的数字是否为奇数
function isOdd(num) {
return num % 2 !== 0
思路二:递归
var numbers = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
function oddCounter(numbers) {
var first = isOdd(numbers[0]) ? 1 : 0
if (numbers.length <= 1) return first
return first + oddCounter(numbers.slice(1))
oddCounter(numbers) // 5
// 工具函数,判断传入的数字是否为奇数
function isOdd(num) {
return num % 2 !== 0
两种思路都能解决问题,但背后的思维方式却截然不同。
循环的逻辑是:一个一个数,非常符合人类的脑回路,就像你要数一数排队买奶茶的队伍中有多少个女孩子一样,从头数到尾一遍呗。
相比之下,递归的路子就有点野了:让队伍的第一个人确认一下自己的性别,如果是女的就在心里就记住自己是 1,否则是 0,接着拍拍第二个人的肩膀让 TA 做同样的事情,一直传递到队尾最后一人,递归的「递」就完成了,这时候队伍里的每个人都知道自己是 1 还是 0。轮到「归」了:从队伍的最后一个人开始,把自己的数字告诉前面那人,前面那人负责把自己的数字和被告知的数字相加,并把相加结果告诉给前面的人,前面的人再相加.....直到回到队首第一人,这人一加,搞定。
递归的秘诀
尽管大多数人对递归的第一印象是烧脑,但递归的本意却是让逻辑变得简单。看循环的代码符合直觉,但总是需要脑子跟着循环走几圈,而同样的问题,递归处理的只需要一个最小的可重复逻辑,显得简洁优雅。当然,优雅不优雅,有个很重要前提:
不要人肉递归,为难自己。这是递归的一大思维误区,当我们看递归代码时,总是忍不住跟着递归一遍又一遍,简单的场景还好,复杂一些的,往往进得去出不来了。
递归的秘诀有两点:
找到最小可重复步骤
找到终止条件
可重复意味递归调用的每一步,做的事情都一摸一样,且最终答案由这些重复的步骤组成。用上述算奇数的例子来说,最小可重复步骤是判断当前数字的奇偶性,并与前一轮递归的结果相加。
递归不能无休止执行下去,需要一个终止条件,这个例子中,终止条件是数组的个数小于一个,说明都「递」完了,该「归」了。
知道这两点,就足够编写出递归代码了(参考开头例子)。
递归的弱点
递归很强大,但一直有个致命弱点 -- 太占内存。算奇数的例子中,除了搞清楚奇偶性之外,每一轮调用还需要和上一轮调用的结果相加,这意味着,程序运行的每一步,都要保留着前面所有步骤的结果以供归化的时候相加。保存这些调用结果是需要内存的,在我们的例子中,数组里只有 10 个数字,如果是 100 万个呢?这时候递归程序就会变成洪水猛兽,把机器性能榨干。
说得专业一些,程序调用会形成一个调用栈(Call Stack),而每一步调用都是一个栈帧(Stack Frame)。比如如下程序:
function add(a, b) {
return a + b
function printSum(a, b) {
var s = add(a, b)
console.log(s)
printSum(1, 2)
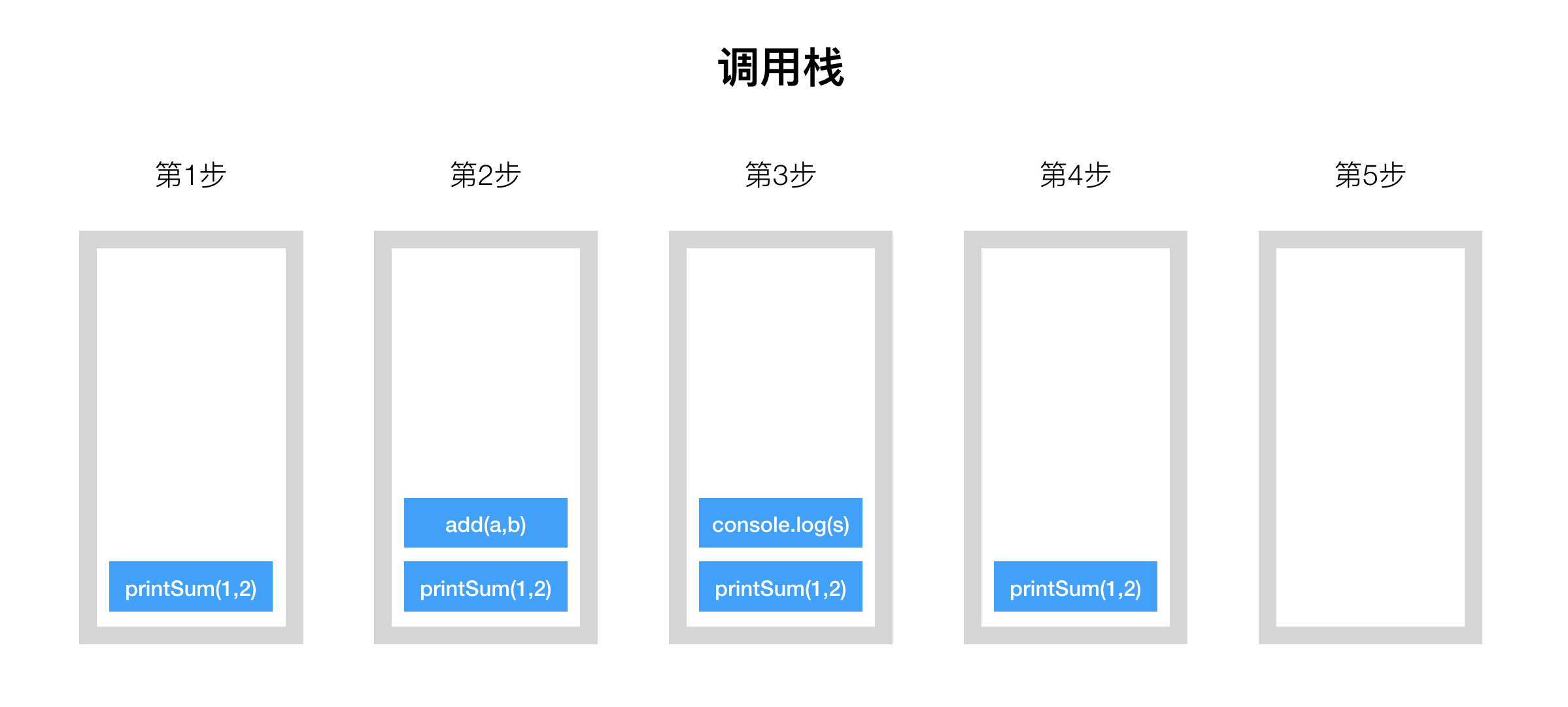
程序执行的调用栈示意如下:
想象一下我们的递归程序,每一步调用都像积木一样叠加到前一个栈帧上,越叠越高。只有触发终止条件后,才会从上往下一个个移除栈帧(出栈),移除的过程是「归」的过程,具体到我们程序中,就是和前一步的调用结果相加,一直「归」到第一步,程序完成并退出。
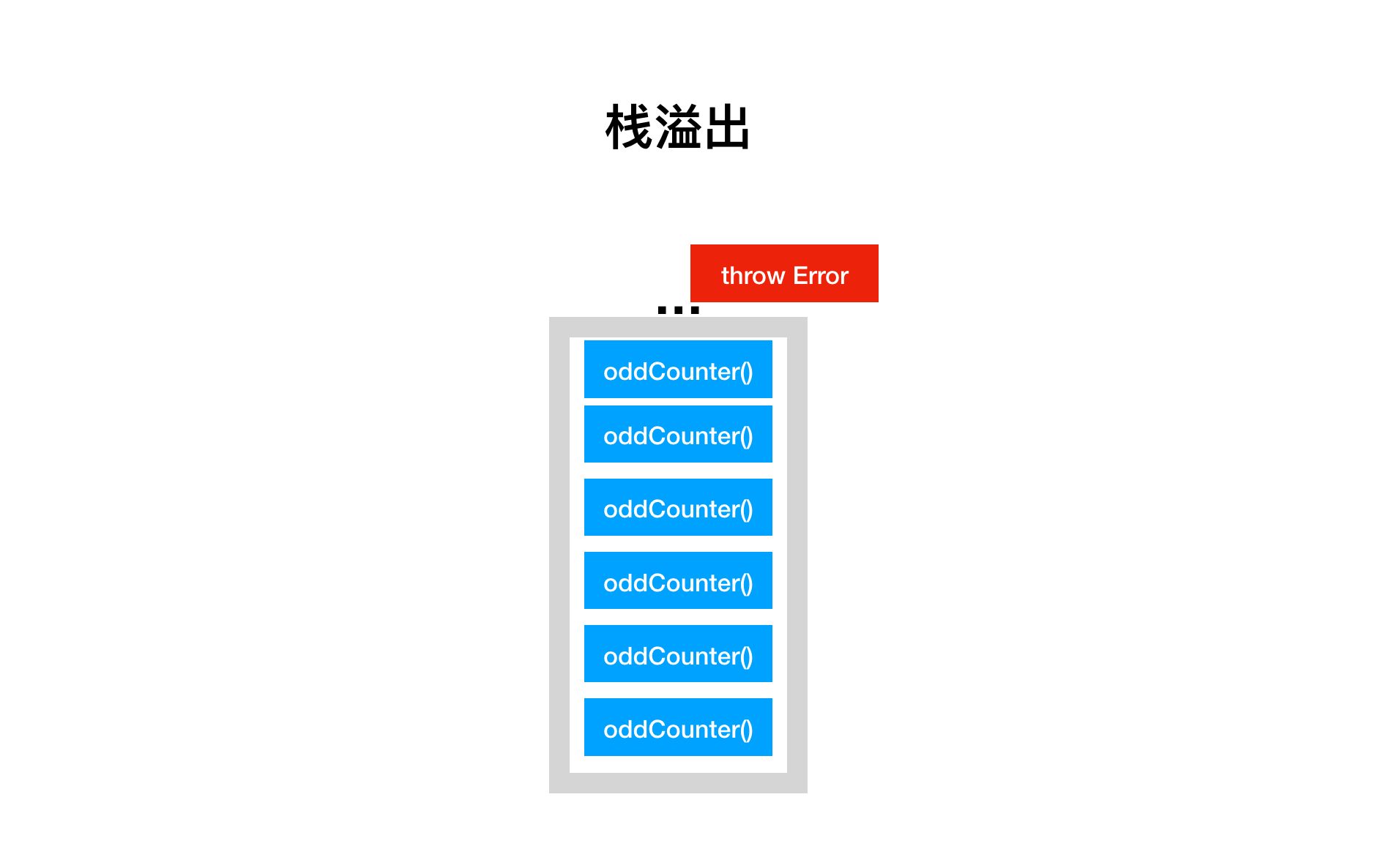
可以想象,如果数据规模非常大,这个栈会叠加得冲破天际,为了防止这种情况发生,程序设置一个递归调用的深度限制,如果超出这个限制,就会报错中止运行,称之为栈溢出(Stack Overflow)。
怎么办,难道递归就只能处理一些小规模的计算吗?
尾调用优化
递归之所以占内存,罪魁祸首是保留前面的调用栈。拿开头的例子说,要算奇数的个数,递归每一轮的计算结果都要保存下来,等待最终归化的时候相加。反应在代码中:就是 return 语句中的 first,这个first 在每一轮递归计算中都存在,内存里始终有她的位置,不能释怀:
// ...
function oddCounter(numbers) {
var first = isOdd(numbers[0]) ? 1 : 0
if (numbers.length <= 1) return first
return first + oddCounter(numbers.slice(1)) // 每一轮都要保存 first 在内存中
要解决这个问题,我们需要改造一下递归函数 -- 在每一轮递归的时候把 first 当作参数传入 oddCounter
function oddCounter(numbers, total = 0) {
total += isOdd(numbers[0]) ? 1 : 0
if (numbers.length <= 1) return total
return oddCounter(numbers.slice(1), total)
改造之后,oddCounter函数在调用时变得独立,不再依赖前一步的执行环境,因为函数内部处理好了加总计算,不用等待每次归化的时候加总。如果原来的递归方法像是搭积木,越搭越高,上面的积木依赖下面所有的积木提供支撑,改造后的递归就像击鼓传花,传到哪里算哪里,对每个人来说把花传走就和自己没关系了。
对函数来说,既然前面的调用栈和现在没关系了,也就自然不需要保存了,每一轮算好自己就好,这就叫「尾调用优化(Tail Call Optimization)」,意味着最后一次(尾巴)递归调用的返回结果,就是最终结果。
用「蹦床」解决栈溢出问题
要注意的是,尾调用优化需要编程语言层面提供支持,拿 JavaScript 来说,在 ES6 中,使用严格模式时,会启动尾调用优化。前提是 -- 符合尾调用的写法,一个标准的尾调用就像return oddCounter(numbers.slice(1)),return 一个函数的计算结果,没有其他乱七八糟的东西。
如果我们的程序运行在不支持尾调用优化的环境怎么办?直接的办法是把递归改写成循环,但递归和循环风格迥异,这样程序的改动量很大,有没有一种办法,既可以保留递归的代码风格,又能防止栈溢出呢?
有的。容我介绍trampoline(弹簧床) ,代码如下:
function trampoline(fn) {
return function trampolined(...args) {
var result = fn(...args)
while (typeof result === "function") {
result = result()
return result
trampoline接收一个普通函数,返回一个蹦床函数。蹦床函数只做一件事情,就是调用接收的函数 -- 如果返回值是函数,继续调用,直到返回值是非函数,return 这个值。听起来和蹦床没什么关系,不着急,蹦一下看看 -- 如果把oddCounter传入 trampoline:
const oddCounter = trampoline(function oddCounter(numbers, total = 0) {
total += isOdd(numbers[0]) ? 1 : 0
if (numbers.length <= 1) return total
return () => oddCounter(numbers.slice(1), total) // !!这里变成 return 一个函数
oddCounter(numbers)
把原先 oddCounter 的返回语句包在一个函数里返回,trampoline 只要遇到返回值是函数,会执行这个函数,直到返回非函数值 -- 变量 total 的值 -- 想象一下整个程序执行的过程,只要递归的终止条件不满足,程序会返回一个函数,trampoline马上执行这个函数,而这个函数干的事情,恰恰就是不断调用 oddCounter ,和递归的效果一摸一样,不同的是,程序只保留一个调用栈,不会产生栈溢出问题。整个过程就像蹦床一样,遇到函数,执行,返回函数,执行,返回函数,执行... 上上下下的。
trampoline本质上是一个 while 循环,但保留了递归程序的代码风格,只不过把返回值包在一个函数里返回,如果今后的某个时候,程序运行在支持尾调用的环境中,可以很方便得去掉trampoline,拥抱递归。
递归和循环是解决问题的两种不同思路
写递归程序要重点在于找到最小可重复步骤和终止条件
递归程序可能会产生栈溢出问题,「尾调用」可以防止栈溢出
在不支持「尾调用」的环境,可以把递归改成循环代码
trampoline可以在不改变递归代码风格的情况下把程序改为循环逻辑