关于 js 中的浮点计算 | 百度EUX

😄 阅读本文需要的：

能将十进制的整数或小数换算成二进制且知道原理

知道原码补码反码，且掌握二进制的加减

有好奇心有耐心

前几天偶然跟人家聊到 javascript 有一个很好玩的事情， 0.1 + 0.2 = 0.30000000000000004 。稍微有经验大概能反应出来这是存储时数据长度截取产生的原因，但是具体是计算机怎么计算的呢，自己也解释不清，于是带着好奇稍微探索了一下。（ps：实际上并不是只有 javascript 存在这种问题，具体可以看看 http://0.30000000000000004.com/ 这个网站。）

浮点数在计算机中的存储

IEEE标准

首先科普一下 js 中使用的二进制浮点数算术标准 IEEE_754 他采用的存储格式为：

E =  (-1)^1 × M × 2^E

(-1)^s表示符号位，当s=0，V为正数；当s=1，V为负数。
M表示有效数字，大于等于1，小于2。
2^E表示指数位。

举例来说，十进制的 5.0，写成二进制是 101.0，相当于 1.01×2^2。那么，按照上面 V 的格式，可以得出 s=0，M=1.01，E=2。十进制的 -5.0，写成二进制是 -101.0，相当于 -1.01×2^2。那么，s = 1，M = 1.01，E = 2。

存储格式

对于32位的浮点数，最高的1位是符号位s，接着的8位是指数E，剩下的23位为有效数字M。

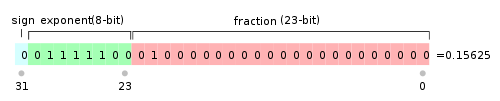
对于64位的浮点数，最高的1位是符号位S，接着的11位是指数E，剩下的52位为有效数字M。

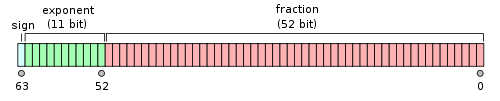
这里只简单说一下第一种情况存储时的一些点：

尾数 M

IEEE 754规定，在 计算机内部保存M时，默认这个数的第一位总是1，因此可以被舍去，只保存后面的xxxxxx部分 。比如保存 1.01 的时候，只保存 01，等到读取的时候，再把第一位的 1 加上去。这样做的目的，是节省 1 位有效数字。以 32 位浮点数为例，留给 M 只有 23 位，将第一位的 1 舍去以后，等于可以保存 24位有效数字。

指数E

指数 E 的情况稍微复杂一点点。

首先，E为一个无符号整数）。这意味着，如果 E 为 8 位，它的取值范围为 0~255；如果 E 为 11 位，它的取值范围为 0~2047。但是，我们知道，科学计数法中的 E 是可以出现负数的，所以 IEEE 754规定，E的真实值必须再减去一个中间数，对于8位的E，这个中间数是127；对于11位的E，这个中间数是1023 。

比如，2^10 的 E 是10，当保存成 32 位浮点数时，必须保存成 10 + 127 = 137，即 10001001。如果要保存成 64 位浮点数的时候，就会保存成 10 + 1023 = 1033，即 10000001001。

然后，指数E还可以再分成三种情况：

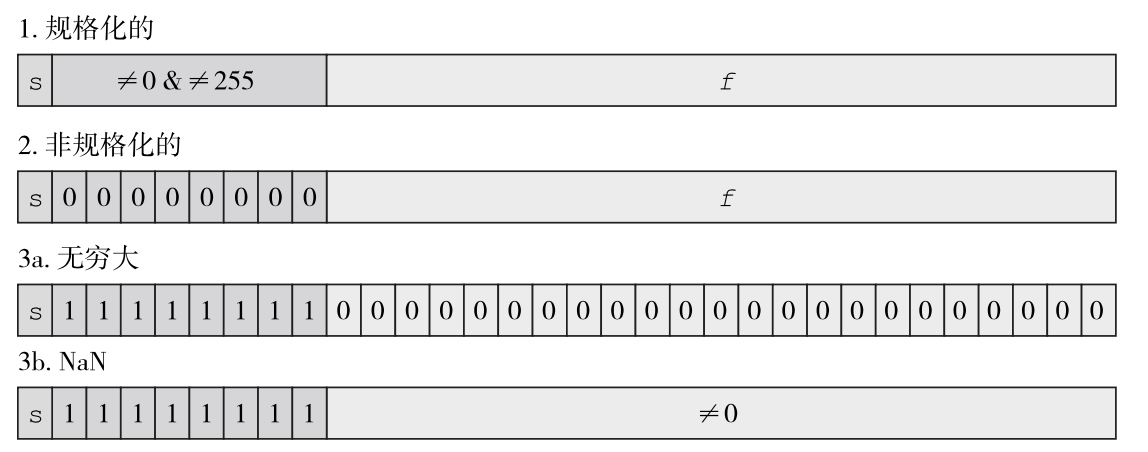
E 不全为 0 或不全为 1。这时，浮点数就采用上面的规则表示，即指数 E 的计算值减去 127（或1023），得到真实值，再将有效数字 M 前加上第一位的 1。
E 全为 0。这时，浮点数的指数E等于 1-127（或者1-1023），有效数字M不再加上第一位的 1，而是还原为 0.xxxxxx 的小数。这样做是为了表示 ±0，以及接近于 0 的很小的数字。
E 全为 1。这时，如果有效数字 M 全为0，表示±无穷大（正负取决于符号位s）；如果有效数字M不全为0，表示这个数不是一个数（NaN）。

浮点数转换为二进制方法

浮点数转换成二进制，我们要将整数部分和小数部分分开，大概就是整数部分采用除2取余倒叙记录，小数部分采用乘2取整顺序记录。具体例子和实现方式可自行搜索。

以 0.1 为例，0.1的二进制

    0.1
x     2
-------
    0.2     0
x     2
-------
    0.4     0
x     2
-------
    0.8     0
x     2
-------
    0.6     1
x     2
-------
    0.2     1
------- 又从0.2开始循环了

于是，我们得到了 0.1 的二进制表示，为 0.0001100110011(0011循环) ，即 1.100110011(0011) * 2^-4 在计算机中的存储表达里，符号 s=0，尾数 M = 1.100110011(0011)，阶码 E = -4 ，实际存储为 -4+1023 = 1019 的二进制 1111111011 。由于 javascript 是双精度的，所以 0.1 在计算机中存储格式为：

0  01111111011  1001100110011001100110011001100110011001100110011010
--------------------------------------------------------------------
s  exp(11位)     frac(52位，注意存储时候前面的1会舍去，最后一位进1)

同理，0.2 的二进制表示为 0.001100110011(0011循环) ，即 1.100110011(0011)*2^-3 在计算机中的存储表达里，符号 s=0，尾数 M = 1.100110011(0011)，阶码 E = -3 ，实际存储为 -3+1023 = 1020 的二进制 1111111100 。在计算机中存储格式为：

0  01111111100  1001100110011001100110011001100110011001100110011010
--------------------------------------------------------------------
s  exp(11位)     frac(52位，注意存储时候前面的1会舍去，最后一位进1)

运算

存储讲完，接下来就该聊下浮点数的加减运算了，它一般有6个步骤完成，先补充一下理论知识：

（1）对 0 、 Infinity 和 NaN 操作数作检查，若有一个操作数为NaN则直接返回NaN;若有一个操作数为0则直接返回另一个操作数;若有一个操作数为Infinity,若另一个操作数也是Infinity且符号相同则返回第一个操作数;若另一个操作数也是Infinity且符号不同则返回NaN;若其他情况则返回Infinity。

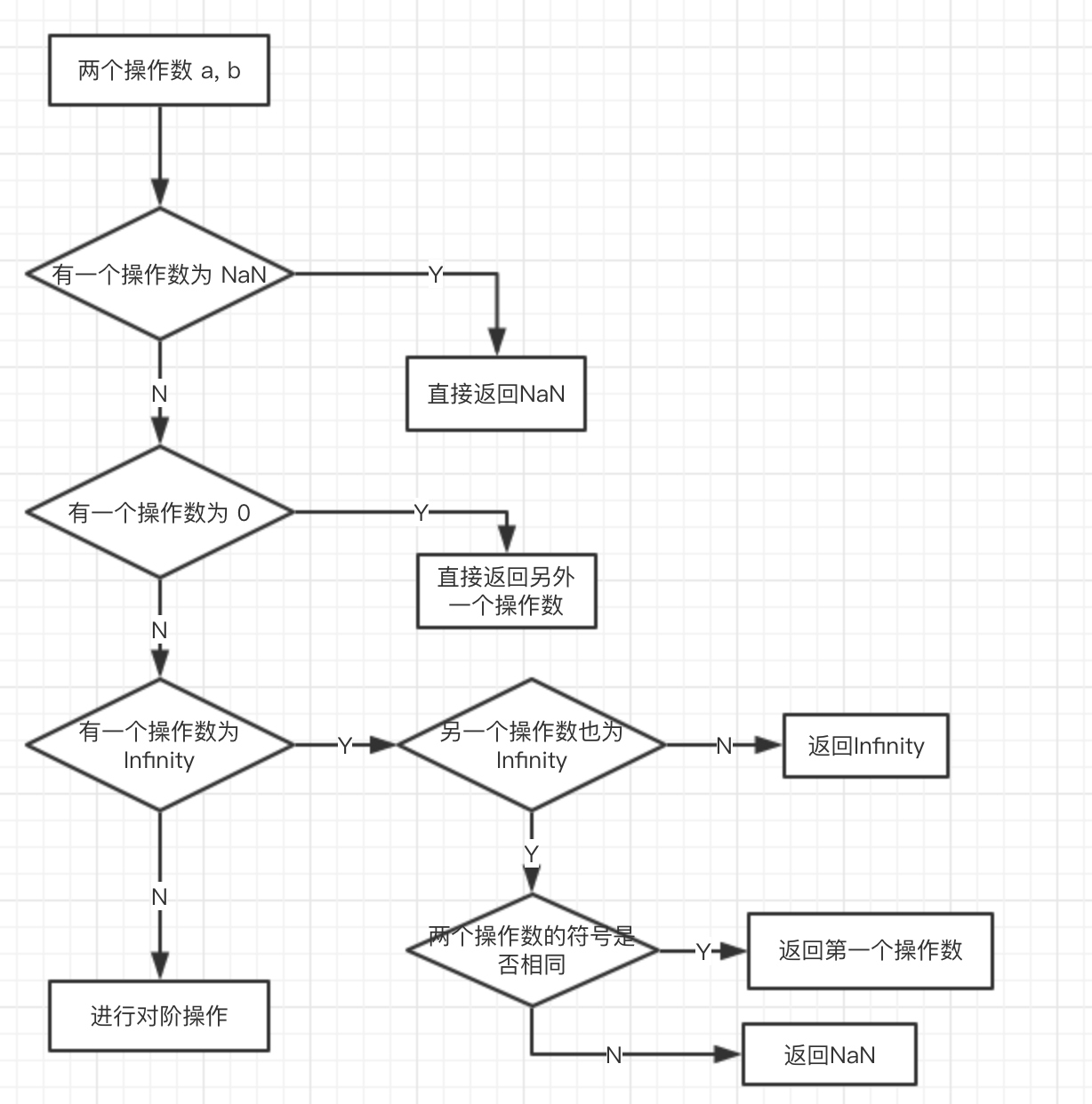
（2）对阶：对阶是将两个进行运算的浮点数的阶码对齐的操作。因为只有使两浮点数的指数值部分相同，才能将相同的指数值作为公因数提出来，然后进行尾数的加减运算。具体方法为：求出两浮点数阶码的差，即 ⊿E＝Ex-Ey ，将小阶码加上 ⊿E ，使之与大阶码相等，同时将小阶码对应的浮点数的尾数右移相应位数，以保证该浮点数的值不变。几点注意：

对阶的原则是小阶对大阶。因为若大阶对小阶，则尾数的数值部分的高位需移出，而小阶对大阶移出的是尾数的数值部分的低位，这样损失的精度更小。
采用补码表示的尾数右移时，符号位保持不变。
由于尾数右移时是将最低位移出，会损失一定的精度，为减少误差，可先保留若干移出的位，供以后舍入处理用。

（3）尾数运算：主要为进行完成对阶后的尾数相加减的相关操作（包含隐藏位），采用双符号法判断是否溢出。

（4）结果规格化，主要分为三种向右规格化：若上一步出现溢出，则尾数右移1位，阶码+1; 向左规格化：若上一步没有出现溢出，且数值域最高位与符号位数值相同，则尾数左移1位且阶码-1，直到数值域最高位为1为止。

（5）舍入处理：由于浮点数无法精确表示所有数值，因此在存储前必须对数值作舍入操作。具体有五种方式，这里我们只谈 IEEE 754 默认的舍入模式： 就近舍入 Round to nearest, ties to even ：就是我们日常所说的四舍五入，当存在两个数一样接近时，取偶数值(如2.4舍入为2，2.6舍入为3；2.5舍入为2，1.5舍入为2)。另外还有 round toward +∞，round toward -∞，round toward 0 这三种模式，有兴趣的可自行查相关资料。

（6）溢出判断：与定点数运算不同的是，浮点数的溢出是以其运算结果的阶码的值是否产生溢出来判断的。若阶码的值超过了阶码所能表示的最大正数，则为上溢，进一步，若此时浮点数为正数，则为正上溢，记为 +∞，若浮点数为负数，则为负上溢，记为-∞；若阶码的值超过了阶码所能表示的最小负数，则为下溢，进一步，若此时浮点数为正数，则为正下溢，若浮点数为负数，则为负下溢。正下溢和负下溢都作为 0 处理。

一堆理论扯完之后，我们来看 0.1 + 0.2 的运算过程。原本的 0.1 和 0.2 的二进制表示

0.1 = 1.1001100110011001100110011001100110011001100110011010 * 2^-4
0.2 = 1.1001100110011001100110011001100110011001100110011010 * 2^-3

可以看到，0.1 的阶码为 -4，0.2 的阶码为 -3，依照小阶对大阶的原则，我们需要将 0.1 的阶码变为 -3，因此其尾数部分需要右移一位。对阶之后 0.1 的存储为：

0.1 = 0.11001100110011001100110011001100110011001100110011010 * 2^-3

想右移一位导致尾数需要进行阶段，因为最后一位刚好是0，所以这里直接舍弃，因此 0.1 对阶之后的存储为

0  01111111100  1100110011001100110011001100110011001100110011001101 
--------------------------------------------------------------------
s  exp(阶码-3)   frac

然后我们就可以愉快的进行相加这个运算步骤了：

   0  01111111100  1100110011001100110011001100110011001100110011001101
+  0  01111111100  1001100110011001100110011001100110011001100110011010

计算的话，手动画一画也没啥大问题，不过身为程序员就比较懒了，这里我们写一个二进制相加的方法：

const a = "1100110011001100110011001100110011001100110011001101".split('');
const b = "1001100110011001100110011001100110011001100110011010".split('');
const res = [];
let flag = 0;
for (let i = a.length - 1; i >= 0; i--) {
    const ai = parseInt(a[i]);
    const bi = parseInt(b[i]);
    const cur = (ai ^ bi) ^ flag; // 当前数值 
    flag = (ai + bi + flag) >= 2 ? 1 : 0; // 进位
    res.unshift(cur);
    if (i === 0 && flag === 1) {
        res.unshift(flag);
console.log(res.join(''));
// 10110011001100110011001100110011001100110011001100111

得出：

   0  01111111100   1100110011001100110011001100110011001100110011001101
+  0  01111111100   1001100110011001100110011001100110011001100110011010
-------------------------------------------------------------------
=  0  01111111100  10110011001100110011001100110011001100110011001100111

可以看到发生了进位，此时尾数超过52，因此阶码部分加1（乘以2），即阶码由原来的 -3 变为 -2，所以阶码部分为 01111111101 。而尾数部分右移一位（除以2），进行舍入（最后一位是1因此最低位进位），得到52位新的二进制表示为：

1011001100110011001100110011001100110011001100110011 ~~1 ~~1011001100110011001100110011001100110011001100110100~~~~

所以，最终的计算结果在计算机中的存储表达如下：

0  1111111101  1011001100110011001100110011001100110011001100110100

将其转换成十进制数为：

2^-2 + (1+(1*2^-1 + 0 * 2^-2+1*2^-3+1*2^-4+... ) = 0.3000000000000000444089209850062616169452667236328125

由于精度问题，只取到 0.30000000000000004。

然后看看 0.3.toString(2) 的结果 �

console.log(0.3.toString(2) );