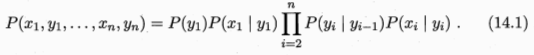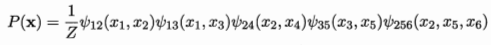推断：利用已知变量推测未知变量的分布。核心：基于观测变量推测出未知变量的条件分布。

给定：关心的变量集合Y、可观测变量集合O、其他变量集合R

生成式模型：考虑联合分布\(P(Y,R,O)\)

判别式模型：考虑条件分布\(P(Y,R\|O)\)

推断：由观测变量值\(P(Y,R,O)\)或者\(P(Y,R\|O)\)，推断得到条件概率分布\(P(Y\|O)\)

概率图模型：

一类用图表达变量相关关系的概率模型

节点：一个或一组随机变量

边：变量间的概率相关关系（变量关系图）

分类：基于边的性质

有向图（贝叶斯网）：使用有向无环图表示变量间的依赖关系

无向图（马尔科夫网）：使用无向图表示变量间的相关关系

状态变量 ：\(y_i\)，第i时刻的系统状态，通常为隐藏的，也称为隐变量(hidden variable)

系统通常在多个状态之间切换，因此状态变量的取值范围称为状态空间，通常是N个可能取值的离散空间。

观测变量 ：\(x_i\)，第i时刻的观测值

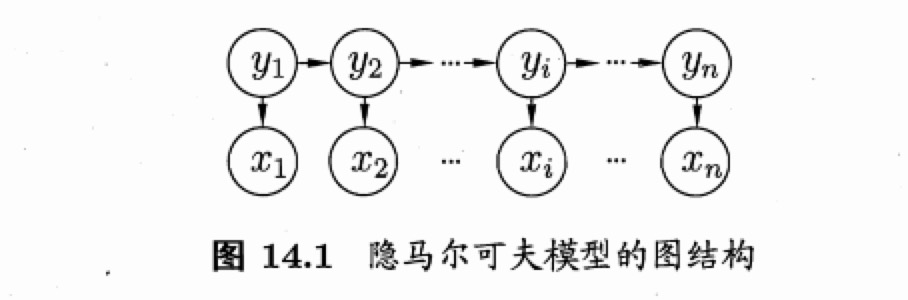箭头：变量间的依赖关系

观测变量：取值仅依赖于状态变量，即\(x_t\)由\(y_t\)确定，与其他状态变量及观测变量的取值无关

t时刻的状态\(y_t\)仅依赖于t-1时刻的状态\(y_{t-1}\)，与其余n-2个状态无关。即 马尔科夫链 ：系统下一时刻的状态仅由当前状态决定，不依赖于以往的任何状态。

所有变量的联合概率分布：

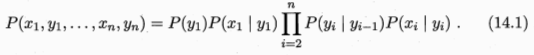模型参数：

状态转移概率 ：模型在各个状态间切换的概率。记为矩阵：\(A=[a_{ij}]_{N\times N}\)，其中的\(a_{ij}=P(y_{t+1}=s_j\|y_t=s_i), 1\le i, j\le N\)表示：在时刻\(t\)状态为\(s_i\)，在下一时刻状态为\(s_j\)的概率

输出观测概率 ：模型根据当前状态获得各个观测值的概率。记为矩阵\(B=[b_{ij}]_{n\times M}\)，其中的\(b_{ij}=P(x_t=o_j\|y_t=s_i), 1\le i, j\le N\)表示：在时刻\(t\)状态为\(s_i\)，则观测值为\(o_j\)的概率

初始状态概率 ：模型在初始时刻各状态出现的概率。记为\(\pi={\pi_1,\pi_2,...,\pi_N}\)，其中\(\pi_i=P(y_1=s_i), 1\le i\le N\)表示：模型的初始状态为\(s_i\)的概率

模型表示：

状态空间Y

观测空间\(\chi\)

3参数：状态转移概率，输出观测概率，初始状态概率，\(\lambda=[A,B,\pi]\)

对于给定参数的模型，产生观测序列的过程：

设置t=1,根据初始状态概率\(\pi\)选择初始状态\(y_1\)

根据状态\(y_t\)和输出观测概率\(B\)选择观测变量取值\(x_t\)

根据状态\(y_t\)和状态转移矩阵\(A\)转移模型状态，即确定\(y_{t+1}\)

若\(t<n\),设置\(t=t+1\)，并转移到第2步，否则停止

3个基本问题：

给定模型与观测序列的匹配程度 。给定模型\(\lambda=[A,B,\pi]\)，如何计算产生观测序列\(x=[x_1,x_2,...,x_n]\)的概率\(P(x\|\lambda)\)。【根据以往的观测，推测当前观测有可能的值，求取概率\(P(x\|\lambda)\)取最大的】

给定模型和观测推断隐藏状态 。给定模型\(\lambda=[A,B,\pi]\)和观测序列\(x=[x_1,x_2,...,x_n]\)，如何找到与此观测序列最匹配的状态序列\(y={y_1,y_2,...,y_n}\)。【语音识别：观测值为语音信号，隐藏状态为文字，根据信号推测最可能的文字】

给定观测序列得到最佳模型参数 。给定观测序列\(x=[x_1,x_2,...,x_n]\)，如何调整模型参数\(\lambda=[A,B,\pi]\)，使得该序列出现的概率最大。【通常不好人工指定模型参数，需根据训练样本学得最优参数】

例子：简单的随机场

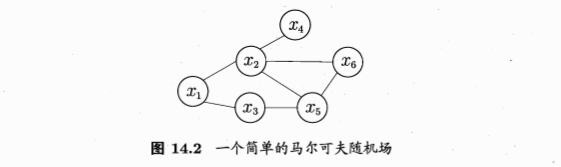团：clique，对于某个子集节点，若其中任意两结点有边连接，则子集为一个团

极大团：maximal clique，在一个团中加入另外任何一个结点都不再形成团。极大团就是不能被其他团所包含的团。

{x1,x2,x3}不构成团，因为x2与x3之间无连接

{x2,x6}是团，但不是极大团，因为可加入x5，从而形成团。同样的{x2,x5},{x5,x6}都不是极大团

极大团：{x1,x2},{x1,x3},{x2,x4},{x3,x5},{x2,x5,x6}

每个节点至少出现在一个极大团中

多变量的联合概率分布：

基于团分解为多个因子的乘积，每个因子仅与一个团有关

n个变量\(x={x_1,x_2,...,x_n}\)，所有团构成的集合是C，\(x_Q\)：团\(Q\subset C\)对应的变量集合

联合概率：\(P(x)=\frac{1}{Z}\prod_{Q\subset C}\phi_Q(x_Q)\)，\(\phi_Q\)是团Q对应的势函数（因子），可对Q中的变量关系进行建模，Z是规范化因子，确保P(x)是被正确定义的概率。

若变量个数很多，团数目很多，很多项的乘积，有计算负担

注意：若团Q不是极大团，则Q必须被一个极大团\(Q'\)包含，即\(x_Q\subseteq x_{Q*}\)

所以联合概率可基于极大团定义

极大团集合为\(C'\)：\(P(x)=\frac{1}{Z*}\prod_{Q\subset C*}\phi_Q(x_Q)\)

对于上面的例子有(5个极大团的联合)：

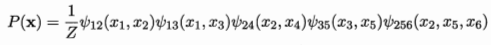条件独立性

从结点集A的结点到B的结点都必须经过结点集C，则A和B被C分离，C称为分离集

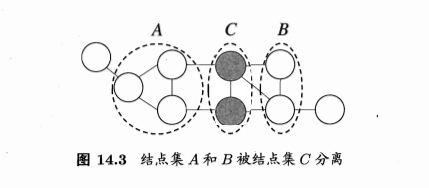全局马尔科夫性：给定两个变量子集的分离集，则这两个变量子集条件独立

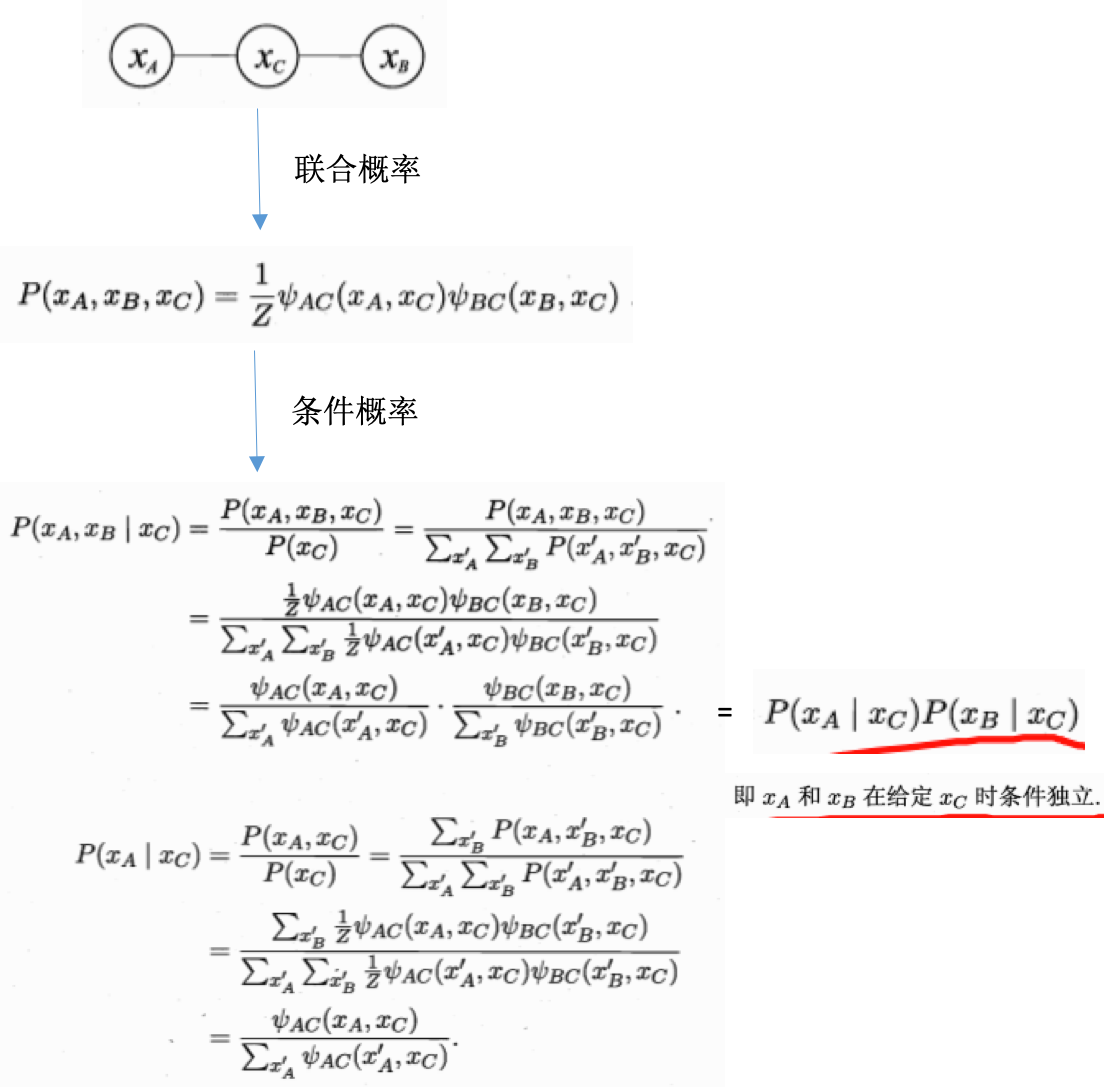【推论】局部马尔科夫性：给定某变量的邻接变量，则该变量条件独立于其他变量

【推论】成对马尔科夫性：给定所有其他变量，两个非邻接变量条件独立

定量刻画变量集\(x_Q\)中变量之间的相关关系

非负函数：指数函数通常用于定义势函数，\(\phi_Q(x_Q)=e^{-H_Q(x_Q)}\)

在所编号的变量取值上有较大函数值

该模型偏好A、C取相同值（势能大），B、C取不同值（势能小）

即：A、C正相关，B、C负相关

联合概率：如果A、C相同，B、C不同，则联合下来将取得较高的联合概率

\(G=<V,E>\)：结点与标记变量一一对应的无向图，若每个变量\(y_v\)均满足马尔科夫性，即：\(P(y_v\|x,y_{V\{v\}})=P(y_v\|x,y_{n(v)})\)，则(y,x)构成一个条件随机场。

链式条件随机场：chain-structured CRF

尤其是标记序列建模时

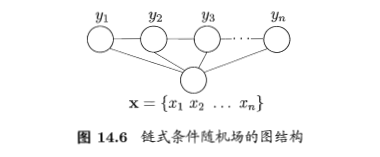条件概率定义：

使用势函数+图结构

边际分布：对无关变量求和或者积分后得到的结果。

例子：马尔科夫网，变量的联合分布表示为极大团的势函数乘积，给定参数\(\Theta\)求解变量x的分布，就是对其他无关变量进行积分的过程，称为边际化（marginalization）

参数估计（学习）：确定具体分布的参数，极大似然法估计或者最大后验概率估计求解

变量集x：分为不相交的\(x_E, x_F\)

推断目标：计算边际概率\(P(x_F)\)或者条件概率\(P(x_F\|x_E)\):

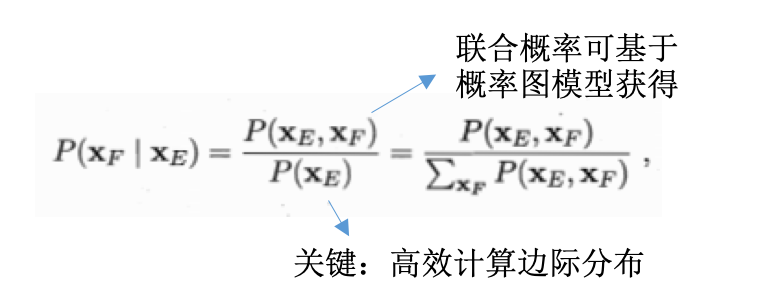概率图推断：

精确推断：计算出目标变量的边际分布或条件分布的精确值。一般计算复杂度极高。

近似推断法：在较低的时间复杂度下获得原问题的近似解。

Metropolis-Hastings

基于拒绝采样来逼近平稳分布p

即每次根据上一轮的采样结果\(x^{t-1}\)来采样获得候选状态样本\(x*\)，但是这个候选样本会以一定的概率被拒绝掉

从状态\(x^{t-1}\)到状态\(x*\)的转移概率为：\(Q(x*\|x^{t-1})A(x*\|x^{t-1})\)，其中\(Q(x*\|x^{t-1})\)是用户给定的先验概率，\(A(x*\|x^{t-1})\)是\(x*\)被接受的概率

若\(x*\)收敛至平稳状态：

吉布斯采样：

gibbs sampling

MH算法的特例

同样适用马尔科夫链获取样本，该马尔科夫链的平稳分布也是采样的目标分布p(x)

给定\(x={x_1,x_2,...,x_N}\)，目标分布p(x)，初始化x的取值

(1) 随机或以某个次序选取某变量\(x_i\)

(2) 根据x中除了\(x_i\)外的变量的现有取值，计算条件概率\(p(x_i\|X_{\bar i})\)

(3) 根据\(p(x_i\|X_{\bar i})\)对样本变量\(x_i\)采用，用采样值代替原值。【所以区别是没有拒绝概率这一条？】

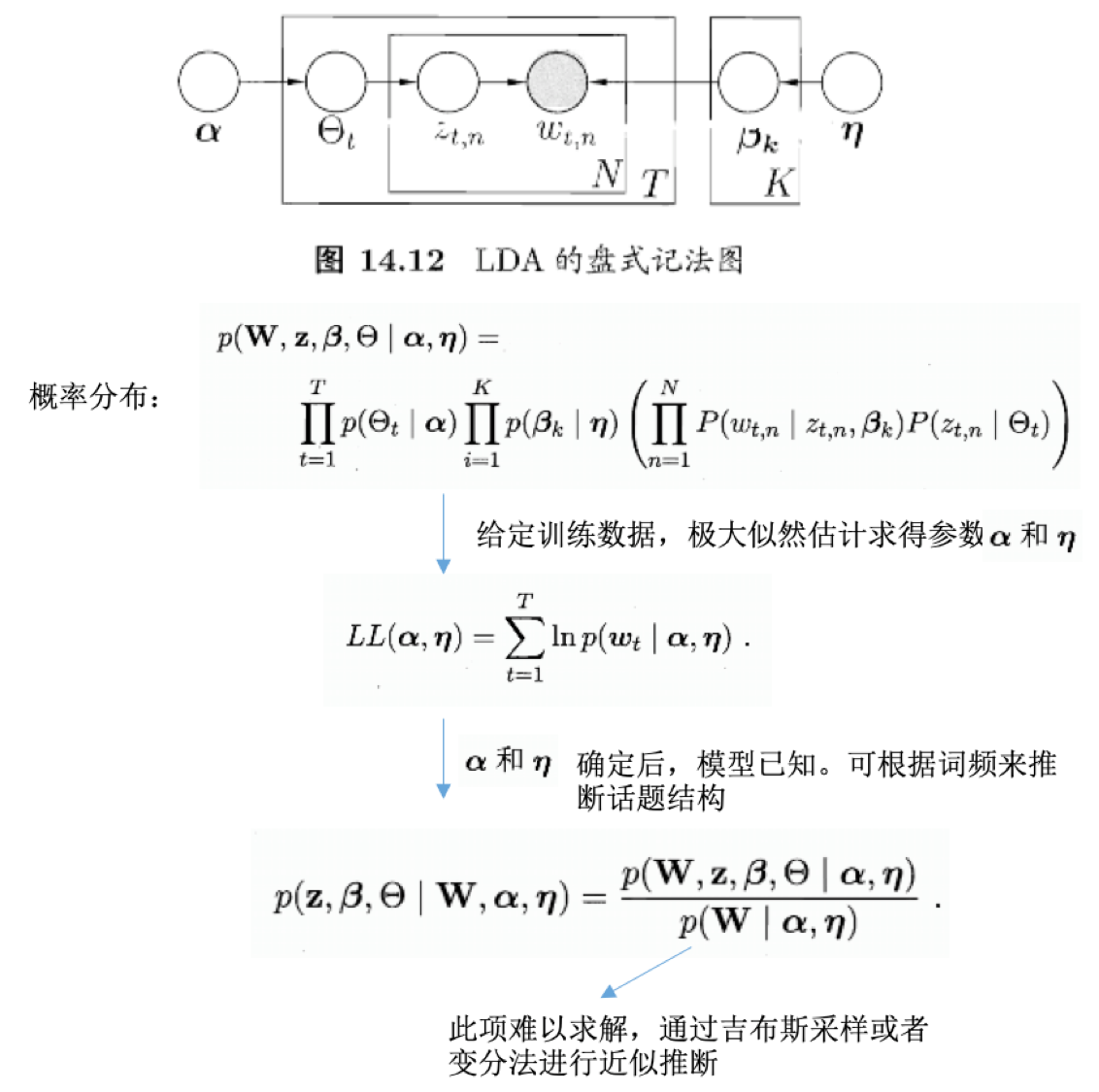
生成式模型的角度看待文档和话题

每篇文档包含多个话题：\(\Theta_{t,k}\)表示文档t中包含话题k的比例，进而通过下面的步骤由话题生成文档t:

根据参数为\(\alpha\)的狄利克雷分布随机采样一个话题分布\(\Theta_t\)

按如下步骤生成文档中的N个词：

根据\(\Theta_t\)进行话题指派，得到文档t中词n的话题\(z_{t,n}\)

根据指派的话题所对应的词频分布\(\beta_k\)随机采样生成词

示例： 这个post 举了一个例子，在python中如何进行LDA分析，这里是重新跑的 notebook ：

目标：分析1987-2016年间发表在NIPS上的文章的文本内容（共6560篇文档），获取话题

工具：sklearn（CountVectorizer统计文本、LatentDirichletAllocation进行LDA分析），pyLDAvis模块进行话题结果的可视化

【1】文本的前期处理不够干净，比如通过词云图，很多无用的符号（et,al,ie,example）是没有去掉的。当然，最后提取的话题的靠前的term也不包含这些。

【2】执行的速度有点慢

【3】这里直接指定的话题数目是5，没有采用评估量作为依据进行挑选（说会在后续的post给出）

【4】如何基于话题结果对每篇文章assign类型？

【5】跑出来的结果不太一样，比如其topic 0是：”model learning network neural figure time state networks using image “，但我这里是”learning data algorithm function set training problem 10 error kernel“。随机数的设定。