贪心算法求解 TSP 旅行商问题及其实现_旅行者问题贪心算法

link管理

链接快照平台

输入网页链接，自动生成快照
标签化管理网页链接

旅行商问题即 TSP（Traveling Salesman Problem），又称为货郎担问题，是数学领域中著名问题之一。假设有一个旅行商人要拜访n个城市，他必须选择所要走的路径，路径的限制是每个城市只能拜访一次，而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。
TSP问题是一个组合优化问题，该问题可以被证明具有NPC计算复杂性 。从图论的角度来看，该问题实质是给定一个带权完全无向图（顶点表示城市，边表示道路，权重是道路的成本或距离），找一个权值最小的 Hamilton 回路。

2. 数学模型

记 G = (V, E) 为赋权图，V = {1， 2 ， ……，n} 为顶点集，E 为边集，各顶点间距离为 C _ij ，已知（C _ij > 0，C _ij = +∞，i，j ∈ V），并设
$s.t.=\begin{cases} \sum_{j ≠ i} c_{ij} = 1 ,& i∈V \\ \sum_{i ≠ j} c_{ij} = 1 ,& j∈V \\ \sum_{i,j∈S} x_{ij} ≤|K|-1 ,& K ⊂V \\ x_{ij}∈\{0, 1\} & i,j∈V\\ \end{cases}$

3. TSP分类

旅行商问题按把不同的分类方法可以分为不同的种类，这里只介绍距离矩阵划分：当 c _ij = c _ji ，(i, j ∈ V)时，问题被称为 对称型旅行商问题 ，反之称为 非对称型旅行商问题 ，非对称旅行商问题可以化为对称型旅行商问题，用对称型的方法求解。当对所有的 i, j, k ∈[1, n]，有不等式 c _ij + c _jk ≥ c _ik ，问题满足三角形不等式的，也称三角型旅行商问题。
旅行售货商问题(TSP)是组合优化领域的经典问题之一,而其中考虑多个旅行商的多旅行商问题(MTSP)是经典的旅行商问题的扩展，多种扩展形式 1 如下：

最小哈密顿链的问题：起点和终点不同；
非对称旅行商问题（asymmetric TSP）：距离矩阵非对称的旅行商问题；
多人旅行商问题（muti-person TSP）：由多人完成旅行的旅行商问题；
多目标旅行商问题（multi-objective TSP）；
依次排序问题（Sequence ordering problem ，SOP）：这类问题是非对称旅行商问题，在给定一系列顶点和距离矩阵下，寻找最短从顶点 1 到顶点 n 哈密顿链，同时满足限制：某些顶点要在一些顶点之前被连接。
载货量受限制的车辆路径问题（Capacitated vehicle routing problem，CVRP）：给定 n-1 个顶点和一个仓库，一直顶点和顶点、仓库和顶点的距离，卡车载货量受限制，卡车每次在部分顶点和仓库之间往返，寻求一条经过所有顶点的最短路线。

二、贪心算法

贪心算法 ，又名贪婪算法，是一种常用的求解最优化问题的简单、迅速的算法。贪心算法总是做出在当前看来最好的选择，它所做的每一个在当前状态下某种意义上是最好的选择即贪心选择，并希望通过每次所作的贪心选择导致最终得到问题最优解。必须注意的是，贪心算法不是对所有问题都能得到整体最优解，选择的贪心策略必须具备 无后效性 ，即某个状态以后的过程不会影响以前的状态，只与当前状态有关。

1. 算法思路

贪心算法以当前情况为基础根据某个优化测度作最优选择，而不考虑各种可能的整体情况，省去了为找最优解要穷尽所有可能而必须耗费的大量时间。贪心算法采用自顶向下，以迭代的方法做出相继的贪心选择，每做一次贪心选择，就将所求问题简化为一个规模更小的子问题，通过每一步贪心选择，可得到问题的一个最优解。虽然每一步上都要保证能获得局部最优解，但由此产生的全局解有时不一定是最优的，所以贪心算法不要回溯。

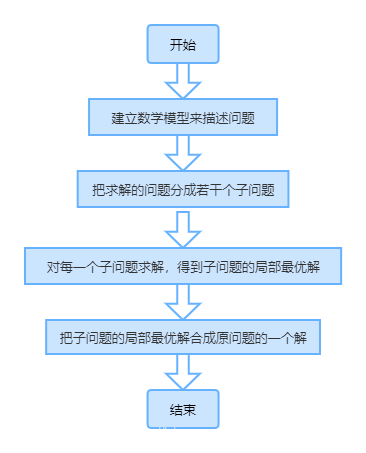
贪心算法求解具有以下性质 2 ：

贪心选择性质 ：一个问题的整体最优解可通过一系列局部的最优解的选择达到，并且每次的选择可以依赖以前作出的选择，但不依赖于后面要作出的选择。这就是贪心选择性质。对于一个具体问题，要确定它是否具有贪心选择性质，必须证明每一步所作的贪心选择最终导致问题的整体最优解
最优子结构性质 ：当一个问题的最优解包含其子问题的最优解时，称此问题具有最优子结构性质。问题的最优子结构性质是该问题可用贪心法求解的关键所在。

2. 算法框架

贪心算法没有固定的算法框架，算法设计的关键是贪心策略的选择，而贪心策略适用的前提是：局部最优策略能导致产生全局最优解。

//问题随机初始解
while(能向总目标前进一步)
	//利用可行的决策，从候选集合中求出可行解的一个解元素；
3. 问题
 
贪心算法也存在如下问题3： 
不能保证求得的最后解是最佳的；
不能用来求最大最小解问题；
只能在某些特定条件约束的情况下使用，例如贪心策略必须具备无后效性等。 
三、贪心算法求解 TSP
 
贪心策略基本思路：从一节点出发遍历所有能到达的下一节点，选择距离最近的节点作为下一节点，然后把当前节点标记已走过，下一节点作为当前节点，重复贪心策略，以此类推直至所有节点都标记为已走节点结束。
 TSP 数据集来自于 TSPLIB 上的 att48.tsp，这是一个对称 TSP 问题，城市规模为48，其最优值为10628。其距离计算方法如下： 
 The edge weight type ATT corresponds to a special “pseudo-Euclidean” distance function. Let x[ i ] and y[ i ] be the coordinates of node i. The distance between two points i and j is computed as follows:
 double dis = sqrt((pow((double)x[i] - x[j], 2) / 10 + pow((double)y[i] - y[j], 2) / 10 ));
 int disInt = (int)dis;
 if(disInt < dis) dis = disInt + 1;
 else dis = disInt; 
具体代码如下： 
/*********************************************************************************************************************
 * TSP 算例来自TSPLIB，att48.tsp 数据集，其中有 48 个城市，距离为伪欧式距离
 * TSPLIB is a library of sample instances for the TSP (and related problems)from various sources and of various types.
 * 目前最佳解总距离为 10628，其中距离的计算方式为 sqrt((x*x + y*y)/10)
 * 使用贪心策略求解，解集总距离为 12861，可见贪心策略只是局部最优解
**********************************************************************************************************************/
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<math.h>
#include<stdlib.h>
#include<time.h>
// 城市数量 N
#define N 48
// 城市距离矩阵
int distance[N][N];
/***********************************************************************
 * Function   ：init()
 * Description：从文件中读取城市坐标，并计算城市之间的距离 distance[N][N] 
 * Input      ：void
 * Output     ：void
 * Return     ：void
 ***********************************************************************/
void init()
	//城市的 x 和 y 坐标
	int x[N] = { 0 };
	int y[N] = { 0 };
	//从 data.txt 文件读取数据
	FILE* fp;
	if ((fp = fopen("..//att48.txt", "r")) == NULL)
		//if ((fp = fopen("..//kroB100.txt", "r")) == NULL)
		printf("can not open the file!");
		exit(0);
	while (!feof(fp))
		int count;
		fscanf(fp, "%d", &count);
		fscanf(fp, "%d%d", &x[count - 1], &y[count - 1]);
	fclose(fp);
	//计算城市之间距离
	for (int i = 0; i < N - 1; i++)
		distance[i][i] = 0;				// 对角线为0
		for (int j = i + 1; j < N; j++)
			double dis = sqrt((pow((double)x[i] - x[j], 2) / 10 + pow((double)y[i] - y[j], 2) / 10));
			int disInt = (int)dis;
			distance[i][j] = dis == disInt ? disInt : disInt + 1;
			distance[j][i] = distance[i][j];
	distance[N - 1][N - 1] = 0;
/***********************************************************************
 * Function   ：TSPGreedyAlgorithm()
 * Description：贪心策略求解 TSP 问题
 * Input      ：void
 * Output     ：TSP 路径和对应的总距离
 * Return     ：void
 ***********************************************************************/
void TSPGreedyAlgorithm()
	//总路程
	int totalDistance = 0;		
	//默认从 0 开始遍历
	int current = 0;	
	//标识城市是否被访问,访问过置为 1
	bool visit[N] = { false };
	visit[0] = 1;
	printf("TSP 路径为：%d ->", 1);
	//遍历 N - 1 次
	for (int i = 1; i < N; i++)
		//设置较大的距离初始值用来选取最近邻
		int min_distance = 0x7fffffff;
		//保存当前最近邻城市
		int temp;
		//循环选取城市
		for (int j = 1; j < N; j++)
			if (!visit[j] && distance[current][j] < min_distance)
				min_distance = distance[current][j];
				temp = j;
		visit[temp] = 1;
		current = temp;
		totalDistance += min_distance;
		printf(" %d ->", temp + 1);
	totalDistance += distance[current][0];
	printf(" %d\n", 1);
	printf("TSP 总距离为：%d\n", totalDistance);
int main()
	init();
	TSPGreedyAlgorithm();
	return 0;
结果如下：
 
 可见，贪心算法求解 TSP 问题只能得到局部最优解，如果需要得到最优解，需要采用局部搜索算法等非精确性算法，作者将在后文中继续介绍其他方法求解 TSP 问题。 
 The multiple traveling salesman problem: an overview of formulations and solution procedures. ↩︎
 
计算机算法设计与分析研究,新华出版社,2015.09. ↩︎
 
计算机算法基础,西南交通大学出版社,2015.02. ↩︎
  
                    贪心算法求解 TSP 问题得到局部最优解的具体实现，数据集来自 TSPLIB 的 att48 数据集。旅行商问题即 TSP（Traveling Salesman Problem），又称为货郎担问题，是数学领域中著名问题之一。
旅行商问题是一个经典的组合优化问题。
经典的TSP问题可以描述为：一个商品推销员要去若干个城市进行商品推销，该推销员从一个城市出发，需要经过所有城市，回到出发地。应如何选择行进路线，以使总的行程最短。
从图论的角度来看，该问题实质是在一个带权完全无向图中，找一个权值最小的Hamilton回路。
由于该问题的可行解是所有顶点的全排列，随着顶点数的增加，会产生组合爆炸。
				问题描述
　　一个旅行家想驾驶汽车以最少的费用从一个城市到另一个城市（假设出发时油箱是空的）。给定两个城市之间的距离D1、汽车油箱的容量C（以升为单位）、每升汽油能行驶的距离D2、出发点每升汽油价格P和沿途油站数N（N可以为零），油站i离出发点的距离Di、每升汽油价格Pi（i=1，2，……N）。计算结果四舍五入至小数点后两位。如果无法到达目的地，则输出“No Solution”。
				贪心算法（又称贪婪算法）是指，在对问题求解时，总是做出在当前看来是最好的选择。也就是说，不从整体最优上加以考虑，他所做出的是在某种意义上的局部最优解。
 所以不能保证最后结果是最优的,只能保证是比较优秀的,但是贪心算法的效率高.
tsp 问题, 旅行商问题，即TSP问题（Travelling Salesman Problem）又译为旅行推销员问题、货郎担问题，是数学领域中著名问题之一。假设




    

				一、求解TSP问题
1、问题描述
TSP问题是指旅行家要旅行n个城市然后回到出发城市，要求各个城市经历且仅经历一次，并要求所走的路程最短。该问题又称为货郎担问题、邮递员问题、售货员问题，是图问题中最广为人知的问题。
2、最近邻点策略
（1）思想：
从某城市出发，每次在没有到过的城市中选择最近的一个，直到经过了所有的城市，最后回到出发城市。
（2）算法设计
设图G有n个顶点，边上的代价存储在二维数组w[n][n]中，集合V存储图的顶点，集合P存储经过的边，最近邻点策略求解TSP问题的算法如下：
（3）算法
				是指一销售商从n个城市中的某一城市出发，不重复地走完其余n-1个城市并回到原出发点，在所有可能的路径中求出路径长度最短的一条。本题假定该旅行商从第1个城市出发。
对每个测试例，第1行有两个整数：n(4≤n≤10)和m(4≤m≤20 ) ，n是结点数，m是边数。接下来m行，描述边的关系，每行3个整数：(i，j)，length，表示结点i到结点j的长度是length。
当n＝0时，表示输入结束。...
（4）在掌握的基础上编程实现TSP问题的具体实现过程。
给出n个城市及任意两城市间的距离，要求旅行家在旅行者n个城市时，各个城市经历且仅经历一次然后回到出发城市，使得所走的路径最短。输出结果，输出时要求有文字说明。请任选一种语言编写程序实现上述算法，并分析其算法复杂度。
实验源代码
public class get {
	public sta
				TSP问题（Traveling Salesman Problem，旅行商问题），由威廉哈密顿爵士和英国数学家克克曼T.P.Kirkman于19世纪初提出。问题描述如下： 
  有若干个城市，任何两个城市之间的距离都是确定的，现要求一旅行商从某城市出发必须经过每一个城市且只在一个城市逗留一次，最后回到出发的城市，问如何事先确定一条最短的线路已保证其旅行的费用最少？
另一个类似的问题为：一个邮递员从邮局
				贪心算法是一种算法策略，它在解决问题时总是做出在当前看来是最好的选择。贪心算法不一定能得到整体最优解，但可以得到局部最优解。对于TSP问题（旅行商问题），贪心算法可以应用于求解思想。其基本思想是从某一个城市开始，每次选择一个最近的城市，直到所有的城市都被走过一遍，并确保经过的路径总距离最短。这种贪心策略称为最近邻点策略。最近邻点策略的算法设计如下：从某城市出发，每次在未经过的城市中选择最近的一个，直到经过了所有的城市，最后回到出发城市。这个算法的时间复杂度为O(n^2)，因为每次选择都需要查找满足贪心条件的最短边。然而，最近邻点策略无法保证得到最优解，尤其是当图中顶点较多且边的代价值分布不均匀时。在这种情况下，最近邻点策略只能给出较好的近似解，但无法保证近似程度。另一种贪心策略是最短链接策略。它的思想是在整个图的范围内选择最短边加入解集合，同时要保证加入解集合的边最终形成一个哈密顿回路。最短链接策略的算法设计如下：每次从剩余边集合中选择最短的边加入解集合，同时满足边是剩余边集合中代价最小的边、加入解集合后不产生回路和分枝。同样地，最短链接策略也不能保证得到最优解。因此，贪心算法可以用于求解TSP问题，但结果可能只是近似解，并不一定是最优解。<span class="em">1</span><span class="em">2</span><span class="em">3</span>
#### 引用[.reference_title]
-  *1* [利用贪心算法求解TSP问题(C语言实现)](https://blog.csdn.net/mahoon411/article/details/105940729)[target="_blank" data-report-click={"spm":"1018.2226.3001.9630","extra":{"utm_source":"vip_chatgpt_common_search_pc_result","utm_medium":"distribute.pc_search_result.none-task-cask-2~all~insert_cask~default-1-null.142^v93^chatsearchT3_1"}}] [.reference_item style="max-width: 33.333333333333336%"]
-  *2* [数学建模贪心算法(贪婪算法)求解TSP问题(C语言程序源码亲测可行)](https://download.csdn.net/download/mahoon411/12393733)[target="_blank" data-report-click={"spm":"1018.2226.3001.9630","extra":{"utm_source":"vip_chatgpt_common_search_pc_result","utm_medium":"distribute.pc_search_result.none-task-cask-2~all~insert_cask~default-1-null.142^v93^chatsearchT3_1"}}] [.reference_item style="max-width: 33.333333333333336%"]
-  *3* [用贪心法解决TSP问题](https://blog.csdn.net/wmy01234/article/details/106020551)[target="_blank" data-report-click={"spm":"1018.2226.3001.9630","extra":{"utm_source":"vip_chatgpt_common_search_pc_result","utm_medium":"distribute.pc_search_result.none-task-cask-2~all~insert_cask~default-1-null.142^v93^chatsearchT3_1"}}] [.reference_item style="max-width: 33.333333333333336%"]
[ .reference_list ]

一、TSP 概述

1. TSP

2. 数学模型

3. TSP分类

二、贪心算法

1. 算法思路

2. 算法框架

3. 问题

三、贪心算法求解 TSP