本文适合有一定热力学基础的同学阅读。
什么是温度
温度标准,简称温标,是量化表示
温度
的方法。因此在谈热力学温标是如何建立的之前,有必要搞清楚到底什么是温度。我们对温度的一切概念都来自于生活中的感官:通过触摸一杯水,我们能感知到水是“冷的”或者是“热的”,所以冷水和热水之间必然存在一种性质上的差别。定义温度实际上就是搞清楚这种性质的差别到底是什么。
去刻画这种性质不容易。学过基础热力学课程的同学会说,温度是分子热运动动能的宏观表现。这句话是对的,下文也将推导出对于理想气体而言这么说的依据。不过这是建立在对系统微观粒子运动的建模上。然而,热力学是门唯象科学,不在乎系统的微观模型到底长什么样。我们必须不借助“微观粒子”这类概念,给出一个宏观的、抽象的温度的定义。
类似数学中通过行和列交换的性质定义了行列式,热力学中通过热平衡状态定义了温度。
在一个绝热的箱子里,把一杯开水和一杯冷水靠在一起,是过了一段时间以后,两个杯子的水和箱子里空气的温度,将变得一致。抽象地讲,相互接触的可以进行热交换的系统,经过很长一段时间以后,总会达到一个
热平衡
的状态,即相互接触的系统之间,在宏观量上没有差别。至于什么是“宏观量”,通俗讲就是那些不考虑系统微观状态的量,比如体积、压强,当然也包括温度本身。而且这个“没有差别”的意思是:现在没有差别,十分钟后没有差别,一万年以后依旧没有差别。这算是进入了热平衡的状态。常识告诉我们:
几个达成了热平衡的系统的充分必要条件是温度一致
。所以温度可以这样定义:
温度是一种决定了系统间是否达到热平衡的性质
。
这种定义方式直接暗示了热平衡的传递性。也就是说,若A和B达到了热平衡(也就是所谓温度一致),A和C达到了热平衡,那么B和C必然也达到了热平衡(因为温度一致)。
如果不存在这种热平衡的传递性,那么热平衡的系统间就可以没有一个共同的性质,或者相反地就算有了这个共同的性质,它们也可能不热平衡(比如上面的B和C)。
然而传递性从逻辑上并不能推导出来:小红和小明是朋友,小明和李狗蛋是朋友,并不能直接推导出小红和李狗蛋是朋友。于是,为了使得传递性成立,人们拿出了热力学第零定律:
Zeroth law of thermodynamics
If two thermodynamic systems are each in thermal equilibrium with a third, then they are in thermal equilibrium with each other.
热力学第零定律
若两个热力学系统均与第三个系统处于热平衡状态,此两个系统也必互相处于热平衡。
(该表述摘自维基百科)
综上:人们通过“热平衡的系统拥有的某个一致的性质”定义了温度,而第零定律保证了这种一致的性质的存在以及其与热平衡可以互推。
温度计与温标
有了温度这个抽象的概念,接下来要考虑的就是如何去表征这个温度。最简单的想法是找到某个东西,它的某个可被我们测量的性质随温度变化而变化,那么我们就可以通过这个可测量的性质去侧面表征温度。大部分温度计利用的是热胀冷缩的原理。让水银温度计与待测量温度的物体接触,使它们达到热平衡。水银温度计里的水银的体积随温度变化,于是就可以通过水银的体积来表征温度。现代的电阻温度计的电阻随温度而变化,所以可以通过电阻来表征温度。
摄氏温标就是在用热胀冷缩来表征温度的时代建立的:一个叫做Anders Celsius的人在一根温度计的玻璃管上标出了水的冰点和沸点,并且把这两点之间平分出100个格来,每个格算1个单位的温度(也就是°C),就有了摄氏温标。那个时候的温标大概都是用热胀冷缩+平分n格的方法建立的。
理想气体方程与绝对零度
温度有没有下限?答案是有的。要认识到这一点需要看理想气体方程:
$$ pV=nR(T+273.15°C) $$
上面的方程的T是在摄氏温标下的温度。可以想象的是如果T比-273.15°C低,那么p和V铁定有一项要是负数,这当然是不可能的。
如果接受了-273.15°C作为最低温,那么就可以把摄氏温标的零点平移到-273.15°C,这样产生的“
理想气体温标
”,就没有负数值了。而在理想气体温标下理想气体方程也就可以写作$ pV=nRT $了。操作上,在相同体积的情况下,对于理想气体,要获得其温度可以利用压强这个参数:
$$T = T_0 \frac{p}{p_0}$$
p_0是一个参考点,描述的是在和待测气体相同体积V下用作“参考”的气体和压强。而待测气体的温度$T$与参考气体的温度$T_0$则满足上面简单的比例关系。
温度与分子平均能量
虽然温度本身是如前文所说的抽象定义的量,但不论如何这种量一定反应着两个系统的物理状态的不同。具体的例子包括上面提到了包括热胀冷缩等的一些宏观现象。这些现象归根结底,都可以解释为系统分子动能随着温度增加而增加,所以系统的温度,实际上反映了系统分子的动能。下面以理想气体为例去说明这一点。
对理想气体建模,首先需要对理想气体的性质加以设定:
-
分子数目很大;
-
分子运动随机且遵循牛顿运动定律;
-
分子的大小(即存在力的作用的距离)远小于分子间的空隙;
-
所有碰撞全是弹性的,而且忽略作用时间。
至此我们得到了一个理想气体的模型。现在开始利用这个模型推导压强、温度、体积、分子速度等等这些量的关系。从一个分子开始:
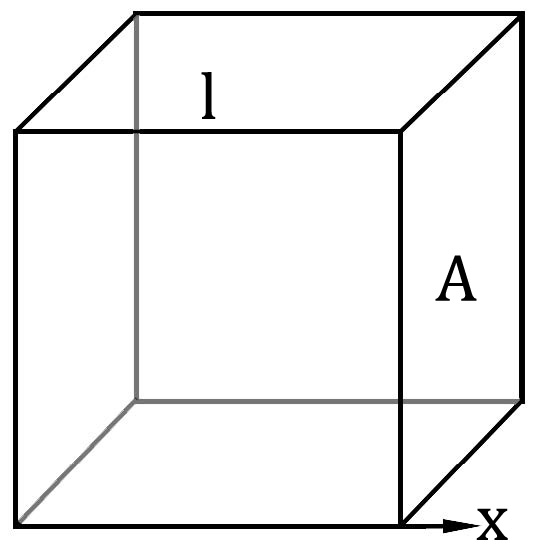
只看这个分子在x轴方向的运动。它碰撞右壁的时间间隔是
$$ \Delta t = \frac{2l}{v_x} $$
每一次碰撞施加的冲量
$$ I = \Delta p = 2mv_x $$
因此右壁平均受这个分子的力的大小为
$$ \bar{F} = \frac{I}{\Delta t} = \frac{m{v_x}^2}{l} $$
上面是单个分子的。现在把所有分子加起来
$$ \bar{F_{all}} = \frac{m({v_{x1}}^2+{v_{x2}}^2+{v_{x3}}^2+\dots)}{l} $$
$$ P = \frac{\bar{F_{all}}}{l^2}
= \frac{m({v_{x1}}^2+{v_{x2}}^2+{v_{x3}}^2+\dots)}{V}
= \frac{2N\bar{E_x}}{V}
上面的$ \bar{E_x} $是所有分子x轴方向的平均动能,N是分子数目。
之后就是大名鼎鼎的能量均分原理:$ E_x = E_y = E_z $,而
$$ E = \frac{1}{2}mv^2
= \frac{1}{2}m({v_x}^2+{v_y}^2+{v_z}^2)
= E_x + E_y + E_z
= 3E_x $$
因此
$$ P = \frac{2N\bar{E}}{3V} $$
又根据理想气体方程$ pV=nRT $,得到了
$$ T = \frac{2}{3} \frac{N_A}{R} \bar{E} $$
这就是理想气体模型下,理想气体温标的温度T与气体分子平均动能E之间的关系。值得注意的是,这个关系是线性的。
卡诺热机的效率
让我们回到正题:“热力学温标”上。
上文已经谈及了一些温标,具体而言,主要是理想气体温标。理想气体温标
依赖理想气体作为介质
。那么能不能找到一种温标,使其不依赖于任何介质,纯粹建立在热力学定律的基础上。这样的尝试产生了所谓的热力学温标。
虽然一开始听上去可能很反常,但是热力学温标的完全确立,是在对热机,尤其是卡诺热机(Carnot heat engine)进行了完整研究后才诞生的。热机,说白了就是热力学里的一种将热转换成功的机器。卡诺热机这个由法国工程师尼古拉·卡诺提出来的热机,是一个
全程可逆
的热机。
热机的一个重要的参数就是热机的效率,其定义是:热机做的功比上热机从热源吸收的热量,也就是
$$ {\eta}_A = \frac{W}{Q_1} $$
上面的A是Arbitrary的意思,$Q_1$就是热机吸收的热量。后文还会用$Q_2$作为热机释放的热量。(注意:这两个Q全都是正值。虽然热力学第一定律给定了一个吸热放热的物理量正负的规范,但是为了方便理解,避免对物理量符号的考虑让整个推倒变得奇怪,本文中用字母表示的能量和功都是正值,符号全都显式给出。)
当然,在继续下去之前还需要稍微提及一些热力学第一定律i.e.能量守恒定律。对于一个热机,要能够一直循环下去,就要保证每次循环结束都能够回到循环开始的初始态。也就是说,热机自身能量储备(内能)没有改变i.e.$ \Delta U = 0 $。热力学第一定律(能量守恒)在这个场景下是这么表述的:
$$ \Delta U = Q_1 - Q_2 - W = 0 $$
上面的W是系统对外做功大小,是系统损失的能量,所以前头是减号。因此 $ W = Q_1 - Q_2 $,
$$ {\eta}_A = \frac{Q_1 - Q_2}{Q_1} = 1 - \frac{Q_2}{Q_1} $$
具体而言,为了建立热力学温标,我们需要先计算卡诺热机的效率。
在
理想气体介质下
工作的卡诺热机的流程是这样的:
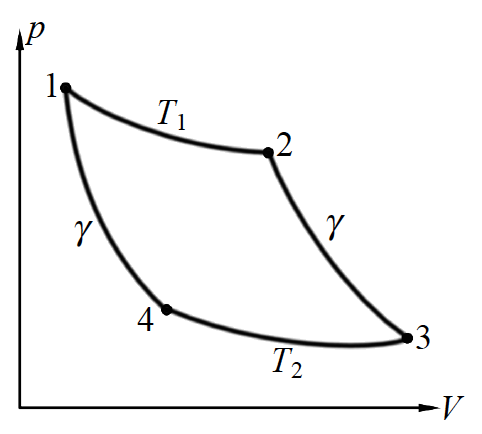
从1出发,此时从高温热源吸热,
可逆地
向2进行
等温膨胀
;之后沿着2→3进行
绝热膨胀
(不与外界交换能量);之后在3→4的过程中与低温热源接触放热,进行
等温压缩
;随后4→1
绝热压缩
(不与外界交换能量),回到初始态。
可逆
是热力学里的一个重要概念,也是卡诺热机的重要特点。说句实话,热力学研究的主要是就可逆(或者所谓准静态,准静态过程都是可逆的)过程。虽然就如字面意思一样,可逆就是指能够向正反两个方向进行。而上面一段对卡诺热机工作流程的描述,其实隐含了“沿着等温线(就是$pV = nRT = constant$的曲线)、绝热线”进行的过程,都是可逆的过程这个意思。
先暂时不管为什么我们必须使用可逆过程,而解决另一个容易造成困扰的问题:为什么顺着等温线的等温过程就是可逆的了?这里提供一个的理解:只要没人推着,就是可逆的;有人推着,就不是可逆的。如果等温过程中的某个状态的(p,V)坐标不在等温线上了,那么这个状态一定是力与力之间不平衡的,于是就会有一种力量(可以是外界的压力,或者气体分子撞击产生的压强)胜过另一种力量驱使气体分子们向等温线靠近。这个靠近过程是由一种
有方向性的
的作用驱使的,自然就不可逆,因为没有“别人推着你向前,你反而向后跑”的可能性。顺着等温线就意味着没有这种外界的作用,你就处在一种“想往前走就往前走,想往后走就往后走”的状态,是为可逆。由绝热方程(全称应该是
绝热过程方程
)描述的绝热过程也是可逆过程,因为其本身是从理想气体方程(全称
理想气体状态方程
)导出的,绝热线上的每一点都符合理想气体状态方程。
(有关于过程方程和状态方程的概念就又可以说上一番了。此处连同绝热过程方程的推倒按下不表。绝热方程的推到可以参见
维基百科的详细叙述
。)
再来谈为什么可逆过程这么重要,或者说,为什么定义热力学温标偏偏要拿出个可逆的卡诺热机?套用托尔斯泰的话做一个回应:可逆的过程都是相似的,不可逆过程却各有各的不可逆法。可逆的情况是系统平衡的状况。平衡是不依赖时间的,所以我们可以通过状态方程很好地把握;而一旦出现不可逆的情况,系统必然就有一种向稳定方向发展的趋势,这个过程就依赖时间、依赖初始状态了,于是就可以五花八门,难以描述。因此,一个可逆的卡诺热机,实际上蕴含着全世界可逆过程所共有的特性,因此才能拿来定义温标。
在解释完可逆的意义与重要性后,继续卡诺热机的效率的讨论。计算卡诺热机的效率,首先要先算出$Q_1$和$Q_2$。
先说$Q_1$,理想气体膨胀对外做功,其功表达为
$$ W_1 = \int F \mathrm{d}x = \int \frac{F}{S} \mathrm{d}(xS) = \int_{V_1}^{V_2} p \mathrm{d}V $$
代入$pV = nRT$,
$$ W_1 = \int_{V_1}^{V_2} \frac{nRT}{V} \mathrm{d}V = nRT_1 \int_{V_1}^{V_2} \mathrm{d}\mathrm{ln} V
= nRT_1 \mathrm{ln}\frac{V_2}{V_1} $$
$V_2 > V_1$,所以显然W是个正值,这一点与我们预期的一致。而且在等温线上,$ \Delta U = 0 $。这是理想气体的性质,理想气体的内能只与其温度有关。温度不变,内能不变。这就是著名的焦耳定律(不是电学那个)。当时焦耳用实验得到了这个结论,但是其实根据理想气体方程和热力学第一定律、热力学第二定律的数学表达,完全可以从数学上得到这个结论(需要用到麦克斯韦变换,也是一件很技术性的事)。因此,$ \Delta U = Q_1 - W_1 = 0 $,$ Q_1 = W_1 = nRT_1 \mathrm{ln}\frac{V_2}{V_1} $。
同理,$Q_2$也可以这么算出来。$ \Delta U = -Q_2 + W_2 = 0 $($W_2$是压缩功,对系统做功,所以是前面取正号)。
$$ W_2 = | \int_{V_3}^{V_4} p \mathrm{d}V | $$
$$ Q_2 = nRT_2 \mathrm{ln}\frac{V_3}{V_4} $$
所以,对应的热机效率就是
$$ {\eta}_R = 1 - \frac{Q_2}{Q_1}
= 1 - \frac{T_2 \mathrm{ln}\frac{V_3}{V_4}}{T_1 \mathrm{ln}\frac{V_2}{V_1}} $$
上面进行的是对等温线的分析,还差两条绝热线的。绝热方程写作$pV^{\gamma} = constant$,也作$TV^{\gamma - 1} = constant$(其实就是把p用$\frac{nRT}{V}$代了一遍)。
因此在2→3,4→1中,有$T_1 {V_2}^{\gamma - 1} = T_2 {V_3}^{\gamma - 1}$,$T_2 {V_4}^{\gamma - 1} = T_1 {V_1}^{\gamma - 1}$。两边取ln后移项,很轻松可以得到$\mathrm{ln}\frac{T_1}{T_2}=(\gamma-1)\mathrm{ln}\frac{V_3}{V_2}=(\gamma-1)\mathrm{ln}\frac{V_4}{V_1}$,也就是说$V_3 / V_2 = V_4 / V_1 = k$,k是一个常数,$V_3 = k V_2$,$V_1 = \frac{1}{k} V_4$。
代入上面的${\eta}_R$,
$$ {\eta}_R = 1 - \frac{T_2 \mathrm{ln}\frac{k V_2}{V_4}}{T_1 \mathrm{ln}\frac{V_2}{\frac{1}{k} V_4}} = 1 - \frac{T_2}{T_1} $$
这就是卡诺热机的效率,其中$T_2,T_1$都是理想气体温标下表示的温度。
热力学第二定律与卡诺定理
费了半天劲倒腾出来一个卡诺热机的效率,乍一看似乎和温标没有半毛钱关系。但是细心的同学应该已经发现了:
$$ {\eta}_R = 1 - \frac{Q_2}{Q_1} = 1 - \frac{T_2}{T_1} $$
$$ \frac{Q_2}{Q_1} = \frac{T_2}{T_1} $$
我们先不管式子的右边是什么形式(因为选取不同的温标会有不同的结果)。就内容上说,这个式子,把热量的比值关系与温度关联了起来。也就是说,用热量定义一种不依赖于介质,只依赖热力学定律的温标成为了可能。
然而在此之前我们要先解决一个问题:我们刚才的推导过程全是建立在以理想气体为介质的卡诺热机身上呀!如果使用这个推导产生的结论,那么我们不是依旧没有摆脱掉介质本身吗?
这个时候,刚才提过的卡诺热机的可逆特性就十分关键了。可逆可以带来的好处,由卡诺定理描述:
卡诺定理
-
在相同的高温热源和低温热源间工作的一切
可逆热机
的效率都相等。
-
在相同的高温热源和低温热源间工作的一切热机中,不可逆热机的效率不可能大于可逆热机的效率。
(定理表述摘自维基百科)
这个定理也是那个卡诺发现的。卡诺作为一个热机工程师,一直在寻找提升热机效率的方法。这个定理,相当是给热机效率的上限盖棺定论了。然而悲催的卡诺就跟梵高这类凄惨的文艺工作者一样,只有死了以后大家才会发现他们的工作多么有价值。
既然全世界可逆热机的效率都一样,那么不管是什么介质,只要是可逆过程,推出来的热机效率,就是全世界所有可逆热机的效率。细心的读者可能发现,在讨论卡诺热机的效率的时候,我在$\eta$下面直接写上了下标R,意为Reversible。
但是这个卡诺定理的证明需要热力学第二定律的帮助:
Second law of thermodynamics
(Clausius statement)
Heat can never pass from a colder to a warmer body without some other change, connected therewith, occurring at the same time.
热力学第二定律
(克劳修斯表述)
不可能把热量从低温物体传递到高温物体而不产生其他影响。
(定理表述摘自维基百科)
为了思维过程的完整,证明过程我还是决定稍微写一下。其实下面的图(摘自
维基百科
)就能很好说明问题了:
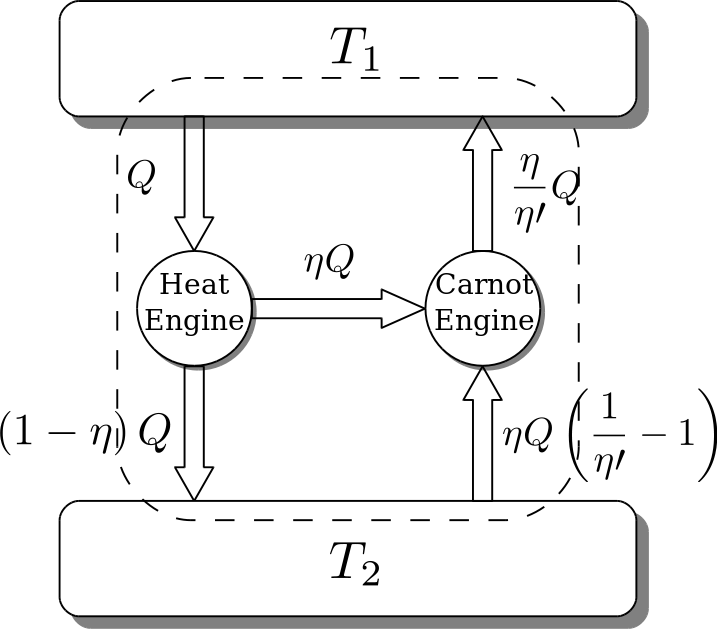
假设存在一个热机,它的效率比可逆热机还要高(就是图中左边那个),那么它吸收热量Q,做$\eta Q$的功,将$(1 - \eta) Q$的热传给低温热源。图中右边是一个可逆热机。既然是可逆热机,有可逆两个字,那么热机就能倒着转。原来是它对外界做功,这次我把左边热机的功$W$输入给它,那么它就从低温热源提取热量,放到高温热源。提取的热量就相当于之前放出的热量$Q_2$,放给高温热源的热量就相当于之前吸收的热量$Q_1$。
记${\eta}_R$为${\eta}'$
$$W = {\eta} Q = {\eta}' Q_1$$
$$Q_1 = \frac{\eta}{{\eta}'} Q > Q$$
相当于还给高温热源的热量大于吸收的热量Q而没有产生其他影响,违反了热力学第二定律的克劳修斯表述。卡诺定理得证。
最后:热力学温标
现在我们已经证明了可逆热机的效率是所有热机的最高效率,而这个最高效率仅依赖热力学第二定律,不依赖于任何介质。所以此刻,用$ \frac{Q_2}{Q_1} = \frac{T_2}{T_1} $去描述温度与热量的关系就没有什么问题了。
那么接下来,让我们忘掉带着我们走到这一步的理想气体温标,而是数典忘祖地用这个式子的左边去定义右边的温标为热力学温标:
$$ T = T_0 \frac{Q}{Q_0} $$
这样我们就知道如何通过不依赖介质的可逆热机来确定温度:在
已知
的$T_0$和$T$间用一个可逆热机联系起来,测量其从$T_0$处吸收/放出的热量$Q_0$和从$T$处放出/吸收的热量$Q$,就能够通过上面的式子得到$T$。
这样定义出来的热力学温标是和理想气体温标等价的。
和理想气体温标不同的地方在于,热力学温标把对“理想气体”的依赖变为了等价的对“热机吸热放热”的依赖,而热机是可以工作在任何介质上的。
当然,大部分课本会以一种更为波折的方式得到热力学温标:对于任意的温标,热机效率与温度都存在一定的关系。把这种关系描述为
$$ \frac{Q_2}{Q_1} = f(T_2, T_1) $$
而$ \frac{Q_3}{Q_2} = f(T_3, T_2) $,$ \frac{Q_3}{Q_1} = f(T_3, T_1) $
同时 $ \frac{Q_2}{Q_1} \times \frac{Q_3}{Q_2} = \frac{Q_3}{Q_1} $。
因此 $ f(T_2, T_1) \times f(T_3, T_2) = f(T_3, T_1) $。
注意了:这个T是任何一种温标,而f是这种温标与$Q_2 / Q_1$的一个转换函数。他们需要满足上面这个关系:$ f(T_2, T_1) \times f(T_3, T_2) = f(T_3, T_1) $。
开尔文选择了一种省事儿的方法,定义$ f(T_2, T_1) \equiv T_2 / T_1 $,得到的就是热力学温标,而这个热力学温标又恰好就是理想气体温标。
结语
经过了一番长篇大论,我们终于从热平衡讲起,经过第零定律,第一定律,卡诺热机的效率,第二定律,卡诺定理,最后达到了热力学温标。可以看出来热力学温标绝对不是一开始学热力学就能迅速理解的东西。要想理解清楚,必须对热力学的基石有比较好的了解。而文中强调的这种从一般到抽象,对数学的高度依赖,也是热力学学科的一大特色,以及为什么热力学那么难懂的原因。
最近偶然要从事一些和温度标定有关的工作,所以写了这篇文详细捋了一遍热力学温标的来龙去脉。内容很多都是我个人的理解,希望大家多指正。
参考文献
-
若干维基百科页面(文中均有标注)
-
卢德馨, University Physics 2nd Edition(没错就是江湖上久负骂名的那本)
标签: none
上一篇:
「これからも、よろしくお願いします。」
下一篇:
经典力学手记:拉格朗日方程
仅有一条评论
兄弟你好。这篇文章写得真是太好了!里面解答了我学热力学以来很多的疑惑。看教科书和wikipedia很多内在的逻辑关系完全搞不清楚。尤其是各种温标的定义和相互关系,哪个是因,哪个是果,以前总感觉是逻辑的死循环,由A定义B,又由B定义A。看了你的文章彻底搞清楚了。
此外,有几点小的建议。
(1) 理想气体的温度不变,则内能不变可以给出物理的解释。因为理想气体很稀薄,所以气体分子间相互作用的势能可以忽略,于是理想气体的内能就是所有分子的总动能。而你在前面已经证明了理想气体的平均动能与温度的关系,因此马上就得到内能只依赖于温度这个结论。
(2) 关于可逆热机的效率,有一个完全不依赖于卡诺热机,只依赖于热力学第二定律的推导。详见著名物理学家Pauli写的教材"Thermodynamics"。
(3) 关于对可逆过程的解释,根据你文章的意思,似乎偏离等温线或者绝热线就不可逆了,这点我觉得不太对。在我看来,P-V图上的任意一个点都是一个热力学平衡态,而P-V图上的任意一条曲线都是平衡态之间的转移,因此都是可逆的。对于真正的不可逆过程,就像你说的过程可能依赖于时间和初始状态,因此系统的状态根本就不在P-V图上。比如一个盒子中间有个隔板,气体开始都集中在左边。当撤去隔板后,到系统平衡的这段时间里,系统根本没有一个良定义的压强P,因此其状态也就不在P-V图上。你文中说的靠近平衡态的过程是由一种“有方向性的作用”驱使的。如果我理解无误的话,这种作用在现代非平衡统计物理中叫做熵力(entropic force)。
不知道你觉得我的理解是否正确?
我最近在做有关非平衡热力学的工作,以后有机会多多交流。再次感谢你的文章帮我解答了这么多疑问!期待你的回复。


