link管理
链接快照平台
- 输入网页链接,自动生成快照
- 标签化管理网页链接
相关文章推荐
|
|
腼腆的匕首 · n行Python代码系列:两行代码调整视频播 ...· 1 年前 · |
|
|
憨厚的瀑布 · 如何以【我穿成了耽美文里的恶毒女配】为开头写 ...· 1 年前 · |
|
|
忐忑的机器猫 · 深入理解ChatGPT:从机器学习到深度学习 ...· 1 年前 · |
|
|
光明磊落的大象 · 堆栈与堆(StackvsHeap):有什么区 ...· 1 年前 · |
|
|
冷冷的红金鱼 · 稳中求进 保时捷迈入电气化新纪元 - ...· 1 年前 · |
本文介绍了一种名为混合专家系统(MoE)的神经网络模型,它适用于数据产生方式不同的数据集。文章详细解释了MoE的工作原理,包括competitiveMoE和cooperativeMoE两种架构,并给出了具体的数学公式。
摘要生成于
,由 DeepSeek-R1 满血版支持,
for j in(0...(d−1)) and i in (0...(c−1))for\ j\ in (0...(d-1))\ and\ i\ in\ (0...(c-1))
f
o
r
j
i
n
(
0
.
.
.
(
d
−
1
)
)
a
n
d
i
i
n
(
0
.
.
.
(
c
−
1
)
)
:
各专家输出为: Vik=wikxV_{ik}=w_{ik}x V i k = w i k x
(其中 wikw_{ik} w i k 为第k个专家模型对第i列输出的权重, VikV_{ik} V i k 为第k个专家对第i列的预测。( wikw_{ik} w i k 添加了bias所以输出为d+1维))
mk=∑i=0c−1Vikm_{k}=\sum_{i=0}^{c-1}V_{ik}
m
k
=
∑
i
=
0
c
−
1
V
i
k
gk=emkT∑kemkTg_{k}=\frac{e^{m_{k}^{T}}}{\sum_{k}e^{m_{k}^{T}}}
g
k
=
∑
k
e
m
k
T
e
m
k
T
输出 yiy_i y i 通过softmax函数转成概率值为:
ysi=eyi∑ieyiy_{si}=\frac{e^{y_{i}}}{\sum_{i}e^{y_{i}}}
y
s
i
=
∑
i
e
y
i
e
y
i
Δwik=λ(yi−ysi)gkx\Delta w_{ik}=\lambda(y_{i}-y_{si})g_{k}x
Δ
w
i
k
=
λ
(
y
i
−
y
s
i
)
g
k
x
Δmk=λ(yi−ysi)(vik−ysi)gkx\Delta m_{k}=\lambda(y_{i}-y_{si})(v_{ik}-y_{si})g_{k}x Δ m k = λ ( y i − y s i ) ( v i k − y s i ) g k x
对于Competitive MoE:
Δwik=λfk(yi−yik)x\Delta w_{ik}=\lambda f_{k}(y_{i}-y_{ik})x
Δ
w
i
k
=
λ
f
k
(
y
i
−
y
i
k
)
x
Δmk=λ(fk−gk)x\Delta m_{k}=\lambda (f_{k}-g_{k})x Δ m k = λ ( f k − g k ) x
yik=eVik∑ieViky_{ik}=\frac{e^{V_{ik}}}{\sum_{i}e^{V_{ik}}} y i k = ∑ i e V i k e V i k
fk=gke∑iyilogyik∑lgle∑iyilogyikf_{k}=\frac{g_{k}e^{\sum_{i}y_{i}logy_{ik}}}{\sum_{l}g_{l}e^{\sum_{i}y_{i}logy_{ik}}} f k = ∑ l g l e ∑ i y i l o g y i k g k e ∑ i y i l o g y i k
混合专家系统(Mixture of Experts)
混合专家系统(MoE)是一种神经网络,也属于一种combine的模型。适用于数据集中的数据产生方式不同。不同于一般的神经网络的是它根据数据进行分离训练多个模型,各个模型被称为 专家 ,而 门控模块 用于选择使用哪个专家,模型的实际输出为各个模型的输出与门控模型的权重组合。各个专家模型可采用不同的函数(各种线性或非线性函数)。混合专家系统就是将多个模型整合到一个单独的任务中。
混合专家系统有两种架构:competitive MoE 和cooperative MoE。competitive MoE中数据的局部区域被强制集中在数据的各离散空间,而cooperative MoE没有进行强制限制。
对于较小的数据集,该模型的表现可能不太好,但随着数据集规模的增大,该模型的表现会有明显的提高。
定义X为N
d维输入,y为N
c维输出,K为专家数,$\lambda $为学习率:
各专家输出为: Vik=wikxV_{ik}=w_{ik}x V i k = w i k x
(其中 wikw_{ik} w i k 为第k个专家模型对第i列输出的权重, VikV_{ik} V i k 为第k个专家对第i列的预测。( wikw_{ik} w i k 添加了bias所以输出为d+1维))
第k个专家输出均值为:
门限模块输出为:
输出 yiy_i y i 通过softmax函数转成概率值为:
对于Cooperative MoE:
Δmk=λ(yi−ysi)(vik−ysi)gkx\Delta m_{k}=\lambda(y_{i}-y_{si})(v_{ik}-y_{si})g_{k}x Δ m k = λ ( y i − y s i ) ( v i k − y s i ) g k x
对于Competitive MoE:
Δmk=λ(fk−gk)x\Delta m_{k}=\lambda (f_{k}-g_{k})x Δ m k = λ ( f k − g k ) x
yik=eVik∑ieViky_{ik}=\frac{e^{V_{ik}}}{\sum_{i}e^{V_{ik}}} y i k = ∑ i e V i k e V i k
fk=gke∑iyilogyik∑lgle∑iyilogyikf_{k}=\frac{g_{k}e^{\sum_{i}y_{i}logy_{ik}}}{\sum_{l}g_{l}e^{\sum_{i}y_{i}logy_{ik}}} f k = ∑ l g l e ∑ i y i l o g y i k g k e ∑ i y i l o g y i k
实验结果:
不同数据集相同k值:
-
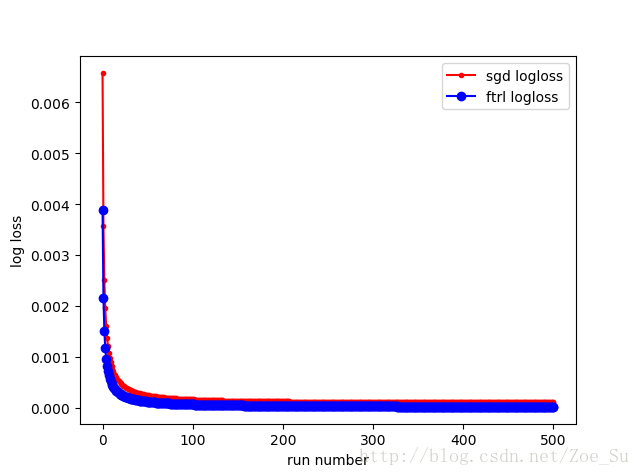
k=2使用线性数据集,采用SGD和FTRL两种训练方式,结果如下:
-
k=2使用非线性数据集,采用SGD和FTRL两种训练方式,结果如下:
相同数据集不同k值:
MoE 理论参考:https://goker.wordpress.com/2011/07/01/mixture-of-experts/实现代码import numpy as np import random import matplotlib.pyplot as pltclass MOE : def __init__ ( self, train_x, train_y, k = 4, lamda =该存储库包含实现专家 模型 的卷积和密集混合的Keras层。 专家层的密集混合物 文件Dense MoE .py包含一个Dense MoE .py层,该层实现了专家 模型 的密集混合: 该层可以与Dense层相同的方式使用。 它的一些主要论据如下: units :输出维数 n_experts :专家人数( ) expert_activation :专家 模型 的激活功能( ) gating_activation :门控 模型 的激活函数( ) 请参阅Dense MoE .py以获取其他参数。 卷积专家层 文件Convolutional MoE .py包含实现专家 模型 的1D,2D和3D卷积混合的Keras层: 其中*表示卷积运算。 这些层可以以与相应的标准卷积层( Conv1D , Conv2D , Conv3D )相同的方式使用。 文件conv_ moe _demo.py包含一个示例,
推荐文章