Machine Learning Goes Causal II: Meet the Random Forest's Causal Brother

link管理

链接快照平台

输入网页链接，自动生成快照
标签化管理网页链接

Why Heterogeneous Treatment Effects?

In Causal Forests, the goal is to estimate heterogeneity in treatment effects. As explained in my previous blog post, a treatment effect refers to a causal effect of a treatment or intervention on an outcome variable of scientific or political interest. For example the causal effect of a subsidized training program on earnings. As individual treatment effects are unobservable, the practice focuses on estimating unbiased and consistent averages of the individual treatment effect. The most common parameter thereof is the average treatment effect, which is the mean of all individual treatment effects in the entire population of interest. However, sometimes treatment effects may vary widely between different subgroups in the population, bet it larger or smaller than the average treatment effect. In some cases, it might therefore be more interesting to estimate these different, i.e. heterogeneous treatment effects.

In most applications it is also interesting to look beyond the average effects in order to understand how the causal effects vary with observable characteristics. (Knaus, Lechner & Strittmatter, 2018)

The estimation of heterogeneous treatment effects can assist in answering questions like: For whom are there big or small treatment effects? For which subgroup does a treatment generate beneficial or adverse effects? In the field of marketing, for example, the estimation of heterogeneous treatment effects can help to optimize resource allocation by answering the question of which customers respond the most to a certain marketing campaign or for which customers is the causal effect of intervention strategies on their churn behavior the highest. Or when it comes to pricing, it might be interesting to quantify how a change in price has a varying impact on sales among different age or income groups.

Where Old Estimation Methods Fail

Estimating heterogeneous treatment effects is nothing new. Econometrics and other social sciences have long been studying which variables predict a smaller or larger than average treatment effect, which in statistical terms is also known as Moderation. One of the most traditional ways to find heterogeneous treatment effects is to use a Multiple Linear Regression with interaction terms between the variables of interest (i.e. the ones which might lead to treatment heterogeneity) and the treatment indicator. In this blog post, I will always assume that the data is from a randomized experiment, such that the assumptions to identify treatment effects are valid without further complications. We then conclude that the treatment effect depends on the variables whose interaction term is statistically significant. For example, if we have only one variable, the regression model would look as follows:

which is dependent on the value of 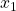$x_1$ and therefore heterogeneous among the different observations.

So why is there a need for more advanced methods to estimate heterogeneous treatment effects? The example above was very simple, it only included one variable. However, usually, we have more than one variable which might influence the treatment effect. To see which variables predict heterogeneous treatment effects, we have to include many interaction terms, not only between each variable and the treatment indicator but also for all possible combinations of variables with and without the treatment indicator. If we have 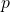$p$ variables and one treatment, this gives a total number of parameters of:

So, for example, if we had 5 variables, we would have to include a total number of 64 parameters into our Linear Regression Model. This approach suffers from a lack of statistical power and could also cause computational issues. The use of a Multiple Linear Regression also imposes linear relationships unless more interactions with polynomials are included. Because Machine Learning algorithms can handle enormous numbers of variables and combine them in nonlinear and highly interactive ways, researchers have found ways to better estimate heterogeneous treatment effects by combining the field of Machine Learning with the study of Causal Inference.

Generalized Random Forests

Over recent years, different Machine Learning algorithms have been developed to estimate heterogeneous treatment effects. Most of them are based on the idea of Decision Trees or Random Forests, just like the one I focus on in this blog post: Generalised Random Forests by Athey, Tibshirani, and Wager (2018).

Generalized Random Forests follow the idea of Random Forests and apart from heterogeneous treatment effect estimation, this algorithm can also be used for non-parametric quantile regression and instrumental variable regression. It keeps the main structure of Random Forests such as the recursive partitioning, subsampling, and random split selection. However, instead of averaging over the trees Generalised Random Forests estimate a weighting function and use the resulting weights to solve a local GMM model. To estimate heterogeneous treatment effects, this algorithm has two important additional features, which distinguish it from standard Random Forests.

1. Splitting Criterion

The first important difference to Random Forests is the splitting criterion. In Random Forests, where we want to predict an outcome variable 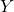$Y$ , the split at each tree node is performed by minimizing the mean squared error of the outcome variable 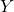$Y$ . In other words, the variable and value to split at each tree node are chosen such that the greatest reduction in the mean squared error with regard to the outcomes 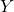$Y$ is achieved. After each tree partition has been completed, the tree’s prediction for a new observation 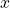$x$ is obtained by letting it trickle through all the way from tree’s root into a terminal node, and then taking the average of outcomes 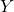$Y$ of all the observations 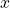$x$ that fell into the same node during training. The Random Forest prediction is then calculated as the average of the predicted tree values.

In Causal Forests, we want to estimate treatment effects. As stated by the Fundamental Problem of Causal Inference, however, we can never observe a treatment effect on an individual level. Therefore, the prediction of a treatment effect is given by the difference in the average outcomes 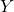$Y$ between the treated and the untreated observations in a terminal node. Without going into too much detail, to find the most heterogeneous but also accurate treatment effects, the splitting criterion is adapted such that it searches for a partitioning where the treatment effects differ the most including a correction that accounts for how the splits affect the variance of the parameter estimates.

Random Forests are usually evaluated by applying them to a test set and measuring the accuracy of the predictions of Y using an error measure such as the mean squared error. Because we can never observe treatment effects, this form of performance measure is not possible in Causal Forests. When estimating causal effects, one, therefore, evaluates their accuracy by examining the bias, standard error and the related confidence interval of the estimates. To ensure that an estimate is as accurate as possible, the bias should asymptotically disappear and the standard error and, thus, the confidence interval, should be as small as possible. To enable this statistical inference in their Generalised Random Forest, Athey, Tibshirani and Wager introduce so-called honest trees .

In order to make a tree honest, the training data is split into two subsamples: a splitting subsample and an estimating subsample. The splitting subsample is used to perform the splits and thus grow the tree. The estimating subsample is then used to make the predictions. That is, all observations in the estimating subsample are dropped down the previously-grown tree until it falls into a terminal node. The prediction of the treatment effects is then given by the difference in the average outcomes between the treated and the untreated observations of the estimating subsample in the terminal nodes. With such honest trees, the estimates of a Causal Forest are consistent (i.e. the bias vanishes asymptotically) and asymptotically Gaussian which together with the estimator for the asymptotic variance allow valid confidence intervals.

Causal Forest in Action

To show the advantages of Causal Forests compared to old estimation methods, in the following I will compare the Generalised Random Forest to a Regression with interaction terms in a small simulation study. I use simulated data to be able to compare the estimated treatment effects with the actual treatment effects, which, as we know, would not be observable in real data. To compare the two algorithms with respect to the estimation of heterogeneous treatment effects, I test them on two different data sets, one with and one wihtout heterogeneity in the treatment effect:

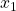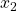This means that in the first data set, all observations have the same treatment effect. In this case, the average treatment effect and the heterogeneous treatment effects are the same. In the second data set, the treatment effect varies with the variables $x_1$ and $x_2$ . 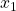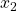Without going into too much detail here (I will probably write a separate blog post only about causal data generating processes), the relationship between those heterogeneity variables ( $x_1$ and $x_2$ ) and the treatment effect is not linear. Both simulated data sets have 20’000 observations containing an outcome variable 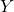$Y$ and 10 covariates with values between zero and one.

To evaluate the two algorithms, the data sets are split in a train (75%) and a test set (25%). For the Causal Forest, I use the causal_forest() from the grf-package with tune.parameters = "all" . I compare this to an lm() model, which includes all variables, the treatment indicator and the necessary interaction terms of the heterogeneity variables and the treatment indicator:

Linear Regression Model for data set with heterogeneity:

where 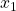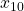$x_1$ – $x_{10}$ are the heterogeneity variables and 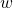$w$ is the treatment indicator (i.e. 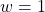$w = 1$ if treated and 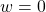$w = 0$ if not treated). As already explained above, we usually do not know which variables affect the treatment effect and have therefore to include all possible interaction terms into the Linear Regression Model to see which variables lead to treatment effect heterogeneity. In the case of 10 variables, as we have it here, this means we would have to include a total of 2048 parameters in our Linear Regression Model. However, since the heterogeneity variables are known in the simulated data, here, I only include the interaction terms for those variables.

Looking at the results, we can see that without heterogeneity, the treatment effect is equally well predicted by the Causal Forest (RMSE of 0.01) and the Linear Regression (RMSE of 0.00). However, as the heterogeneity level increases, the Causal Forest is far more accurate (RMSE of 0.08) than the Linear Regression (RMSE of 0.45). As expected, the Causal Forest seems to be better at detecting the underlying non-linear relationship between the heterogeneity variables and the treatment effect than the Linear Regression Model, which can also be seen in the plots below. Thus, even if we already know which variables influence the treatment effect and only need to include the necessary interaction terms, the Linear Regression Model is still less accurate than the Causal Forest due to its lack of modeling flexibility.

I hope that this blog post has helped you to understand what Causal Forests are and what advantages they bring in estimating heterogeneous treatment effects compared to old estimation methods. In my upcoming blog posts on Causal Machine Learning, I will explore this new field of data science further. I will, for example, take a look at the problems of using classical Machine Learning algorithms to estimate causal effects in more detail or introduce different data generating processes to evaluate Causal Machine Learning methods in simulation studies.

References

Athey, S., Tibshirani, J., & Wager, S. (2019). Generalised random forests. The Annals of Statistics , 47(2) , 1148-1178.

Knaus, M. C., Lechner, M., & Strittmatter, A. (2018). Machine learning estimation of heterogeneous causal effects: Empirical monte carlo evidence. arXiv:1810.13237v2 .

As one of the leading companies in the field of data science, machine learning, and AI, we guide you towards a data-driven future. Learn more about statworx and our motivation. About us

Vielen Dank für Ihre Nachricht. Wir werden uns schnellstmöglich mit Ihnen in Verbindung setzen. Freundliche Grüße Ihr statworx Team