ABSTRACT
As sparse representation of signals has excellent characteristics, it has been applied in several fields of signal processing. However, the computational complexity has become a major obstacle in practical application. Frame theory is a new research direction and can be more flexible representation signal. In this paper, with the characteristics of sparse signal and frameworks, we propose a sparse signal reconstruction algorithm based on ETF, and then simulate and verify it.
Keywords:
Signal Processing, Sparse Signal, Equiangular Tight Frames
基于等角紧框架的稀疏信号重构算法
钱建,张洪峰
杭州电子科技大学通信工程学院,浙江 杭州
Email:
[email protected]
收稿日期:2015年5月10日;录用日期:2015年5月23日;发布日期:2015年5月28日

摘 要
由于信号稀疏表示的优良特性,已被用于信号处理很多领域,但计算复杂成为其实际应用中一大障碍。框架理论是一个新的研究方向,框架可以更为灵活的表示信号。本文结合稀疏信号和框架的特点,提出一种基于等角紧框架(Equiangular Tight Frames, ETF)的稀疏信号重构算法,并通过相应仿真验证。
关键词 :
信号处理,稀疏信号,等角紧框架

1. 引言
在1993年,Mallat和Zhang在研究了小波分析后,提出将信号在过完备原子库上进行分解,然后根据信号本身特点自适应的选取,从而得到信号的稀疏表示 [1] 。但与之发展起来的重构算法具有的高计算复杂度使其在实际应用中受到诸多限制。
为了突破瓶颈,框架应运而生。框架理论是在泛函分析、矩阵理论等相关领域研究基础上,结合实际应用中对“冗余”的需求逐渐发展而来的,是继小波分析后又一个新的研究方向,可看做是基的推广。因为框架不仅继承了正交基的良好性质,而且存在一定的冗余度,而正是这种具有冗余性的线性序列组成的框架,在表示信号时可以更为灵活。
本文在研究压缩采样稀疏信号和框架的基础上,结合两者特点,提出一种基于等角紧框架的稀疏信号重构算法,该方法利用等角紧框架来设计用于检测稀疏信号的测量矩阵,实现对信号更为快速的检测,减少计算量,最后通过仿真实验证明该方法的正确性。
2. 压缩采样理论
近几年,压缩采样(Compressive Sampling,CS)理论 [2] - [5] 成为信号处理中的一个研究热点,该理论指出,对于可压缩或者稀疏的信号,能在远低于奈奎斯特采样速率的情况下,在实现对信号进行采样的同时完成压缩,极大的减少了数据的采集量,节省了存储空间。CS理论表明,如果信号在某个变换域下表现出稀疏性或者可压缩性,那么就能通过一个与变换域不相关的测量矩阵,以远低于奈奎斯特定理所规定的采样率对信号进行采样,而且得到的少量采样值已包含了原信号的足够信息,利用相应的算法就可实现信号的复原。
稀疏分解
使用压缩采样方法的首要条件是信号在某个变换域下具有稀疏性或可压缩性。现假设有一个
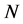 维信号
维信号
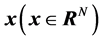 ,并可被
,并可被
 维基向量
维基向量
 表示。那么由这些基向量构成的基矩阵则为
表示。那么由这些基向量构成的基矩阵则为
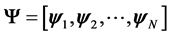 ,
,
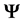 也称为稀疏字典。信号
也称为稀疏字典。信号
 可线性表示为:
可线性表示为:
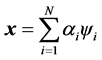 或
或
 (1)
(1)
上式中的
 是信号的时域表示形式,
是信号的时域表示形式,
 称为稀疏矢量,并且
称为稀疏矢量,并且
 是信号在
是信号在
 域的等效表示形式。如果
域的等效表示形式。如果
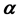 中只有
中只有
 个非零值,其余都是零,且
个非零值,其余都是零,且
 或者
或者
 中只有
中只有
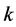 个大系数,其余系数重新排列后按指数级迅速衰减至零,那么就认为信号
个大系数,其余系数重新排列后按指数级迅速衰减至零,那么就认为信号
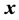 是稀疏的或可压缩的,稀疏度为
是稀疏的或可压缩的,稀疏度为
 。
。
信号通过一个测量矩阵后对信号进行了降维,一个
 维信号
维信号
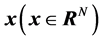 经过一个
经过一个
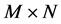 维的测量矩阵
维的测量矩阵
 后,将得到一个
后,将得到一个
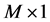 维观测值
维观测值
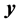 ,
,
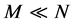 ,用公式表示如下:
,用公式表示如下:
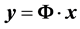 (2)
(2)
将式(1)代入上式可得:
 (3)
(3)
其中,
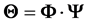 ,是一个
,是一个
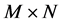 的矩阵,称为恢复矩阵。从式(3)可以看出,信号
的矩阵,称为恢复矩阵。从式(3)可以看出,信号
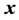 从原本的
从原本的
 维降到了
维降到了
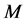 维,大大降低了信号采样点数量。
维,大大降低了信号采样点数量。
为了能从观测值
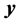 中高概率的重构出原始信号
中高概率的重构出原始信号
 或稀疏矢量
或稀疏矢量
 ,只要恢复矩阵
,只要恢复矩阵
 和稀疏矢量
和稀疏矢量
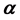 满足Candes和Tao提出的约束等距性质(Restricted Isometry Property,RIP) [6] [7] :
满足Candes和Tao提出的约束等距性质(Restricted Isometry Property,RIP) [6] [7] :
 (4)
(4)
那么就能依据测量值精确恢复出原始信号。
3. 框架
框架是Duffin和Schaeffer在研究非调和傅里叶级数中引入的,是冗余的向量集合,在众多的框架中,某些框架即使缺少部分向量,仍能表示空间中所有元素。若是用该类框架编码数据时,一旦有数据的丢失,不会影响后期数据的恢复,具有很好的鲁棒性。此外,在所有的框架中,紧框架的性能最优,因为该类框架能使编码过程中存在的量化误差达到最小[8] 。
对于希尔伯特空间
 中的有序向量集合
中的有序向量集合
 ,对于任意的
,对于任意的
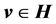 ,若是存在正实数
,若是存在正实数
 ,满足等式:
,满足等式:
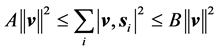 (5)
(5)
则称该向量集是空间
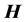 中的一个框架。其中,
中的一个框架。其中,
 和
和
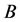 表示该框架的上下限。当
表示该框架的上下限。当
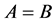 时,则称为紧框架。如果
时,则称为紧框架。如果
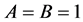 ,那么就称为标准紧框架。
,那么就称为标准紧框架。
现假设存在一个
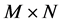 的矩阵
的矩阵
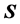 ,如果矩阵
,如果矩阵
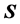 的列向量
的列向量
 满足:
满足:
1) 所有的列向量都存在单位范数,即
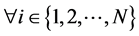 ,
,
 ;
;
2) 列向量之间满足等角关系,即
 ,且
,且
 ,存在
,存在
 ,
,
 为某常数;
为某常数;
3) 列向量是一个紧框架,即
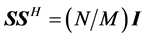 。
。
那么矩阵
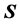 或者
或者
 的列向量构成的集合就称为等角紧框架。而ETF具有比较完美的数学表达形式,性质优良,因此在信号处理方面有着很高的应用价值。
的列向量构成的集合就称为等角紧框架。而ETF具有比较完美的数学表达形式,性质优良,因此在信号处理方面有着很高的应用价值。
4. 基于ETF的稀疏信号重构算法
压缩采样选用的测量矩阵中,等角紧框架在前述意义下是最佳的。如果压缩采样中的恢复矩阵
 具有相同的奇异值,那么它的列向量就是一个紧框架,因此构造一个恢复矩阵对应的矩阵来逼近等角紧框架
具有相同的奇异值,那么它的列向量就是一个紧框架,因此构造一个恢复矩阵对应的矩阵来逼近等角紧框架
 。
。
 (6)
(6)
当采用逼近等角紧框架的矩阵作为测量矩阵时,稀疏信号
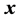 的重构在小稀疏度情况下具有非常简洁快速的过程,具体可描述如下:
的重构在小稀疏度情况下具有非常简洁快速的过程,具体可描述如下:
1) 根据观测值
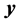 计算
计算
 ,进一步
,进一步
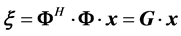 ;
;
2) 对于逼近的等角紧框架,有:
 (7)
(7)
根据矩阵
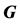 的表达式以及
的表达式以及
 可以得到列矢量
可以得到列矢量
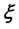 中的第
中的第
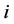 个元素
个元素
 与
与
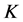 稀疏信号
稀疏信号
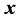 中非零元素
中非零元素
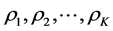 及其位置索引
及其位置索引
 之间有如下关系:
之间有如下关系:
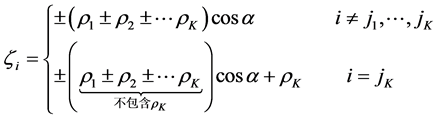 (8)
(8)
由于上式中存在正负号,则矢量
 中的相应元素
中的相应元素
 有
有
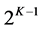 种可能的取值。当小稀疏度时,可以采用统计方法求得元素
种可能的取值。当小稀疏度时,可以采用统计方法求得元素
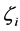 ,再根据式(7)得到对应稀疏信号
,再根据式(7)得到对应稀疏信号
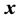 的零元素位置索引,进而确定出对应稀疏信号
的零元素位置索引,进而确定出对应稀疏信号
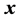 的零元素位置;而对应原始稀疏信号中的非零元素位置,矢量
的零元素位置;而对应原始稀疏信号中的非零元素位置,矢量
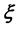 中的相应元素值则处于异类。
中的相应元素值则处于异类。
3) 根据得到的原始稀疏信号中非零元素位置索引,即可从重构字典中找出相应原子,以最小二乘法即可重构原始信号。
5. 仿真实验
我们设计了一个
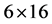 的等角紧框架,把它写成矩阵形式为:
的等角紧框架,把它写成矩阵形式为:
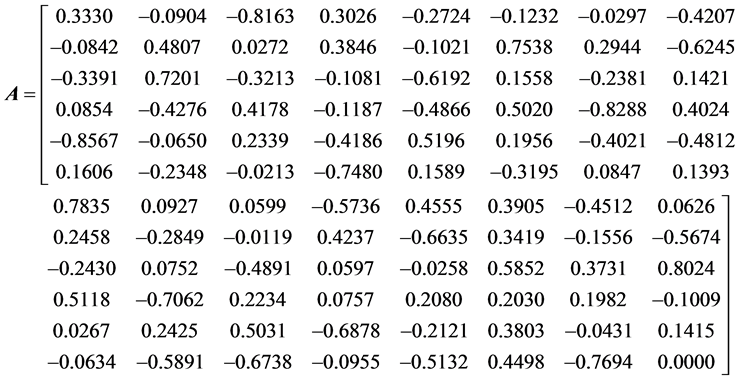
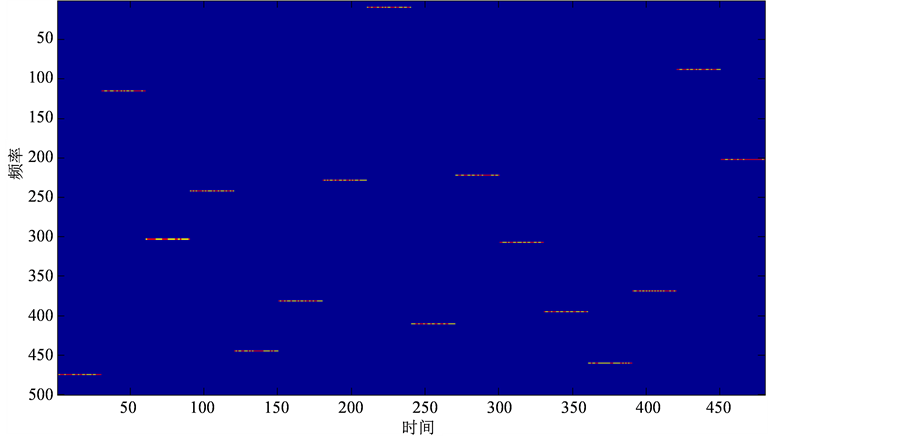
图1
是50个随机频率、随机出现时间、随机驻留时间的干扰信号与一个跳频信号混合后的时频图,可以看出跳频信号图案被严重污染。图2则是按前述重构方法恢复的跳频信号时频图案,该跳频信号的频率是从16个频率的跳频频率集合中随机产生的。
从上图中可以看出,本文提出的重构算法能够准确的恢复出信号,同时对于干扰信号还有一定的抑制。此外,为了定量观察新的稀疏信号重构方法在计算量上的减少程度,
表1
给出了经典的BP算法、OMP算法与新子空间法在运行时间上的对比。在计算机的MATLAB环境下重复运行1000次算法,可以发现新算法具有高得多的计算效率,如果无噪声污染的原始信号稀疏度
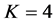 ,则能精确重建的频带压
,则能精确重建的频带压
缩比可以达到
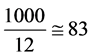 ,且信息测量点数不受
,且信息测量点数不受
 的制约。而相反,同样的信
的制约。而相反,同样的信
息测量数
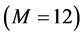 ,OMP和BP算法是不能重构原始信号的。
,OMP和BP算法是不能重构原始信号的。

Figure 1
. Interferential signal frequency hopping spectrogram
图1
. 有干扰的跳频信号时频图
图2
. 恢复后的跳频信号

Table 1
. The comparison of BP, OMP and ETF algorithms’ computational efficiency and reconstruction
表1
. BP算法、OMP算法和ETF稀疏重构方法的计算效率与重建性能对比
说明:符号(√)表示正确重建,符号(×)表示重建失败
6. 结束语
本文首先介绍了压缩采样原理及框架理论。利用等角紧框架具有的本身优点,并将其应用到稀疏信号的重构,在理论上证明了该方法的可行性,随后通过仿真实验,在定量上证明该方法的正确性。根据仿真结果可以看出,利用等角紧框架来重构稀疏信号计算将非常简洁、迅速,比传统的OMP算法有着高的多的计算效率,不需要像OMP算法那样进行复杂的内积运算。但存在的缺点也显而易见,由于该方法中对于零元素的位置是利用统计的方法计算得出,在面对大稀疏度时,计算也会变得复杂,耗时严重。因此,该方法在处理大稀疏度时,还需要更为深入的研究,但对于小稀疏度的信号重构有着明显的优势,同时在重构过程中还能一定程度的抑制干扰信号,有着很大的应用价值。
文章引用
钱 建,张洪峰, (2015) 基于等角紧框架的稀疏信号重构算法
Sparse Signal Reconstruction Algorithm Based on ETF.
计算机科学与应用
,
05
,165-170. doi:
10.12677/CSA.2015.55021
参考文献 (References)
-
1
. Shi, Y.H. and Eberhart, R.C. (1998) A modified particle swarm optimizer. IEEE International Conference on Evolu-tionary Computation, Anchorage, 4-9 May 1998, 69-73.
-
2
. Donoho, D. (2006) Compressed sensing. IEEE Transac-tions on Information Theory, 52, 1289-1306.
-
3
. Candes, E.J. and Wakin, M.B. (2008) An introduction to compressive sampling. IEEE Signal Processing Magazine, 25, 21-30.
-
4
. 黄琼, 屈乐乐, 吴秉横, 等 (2010) 压缩感知在超宽带雷达成像中的应用. 电波科学学报, 1, 77-82.
-
5
. 叶蕾, 杨震 (2010) 基于压缩感知的语音压缩与重构. 南京邮电大学学报(自然科学版), 4, 57-60.
-
6
. Candes, E.J. (2008) The restricted isometry property and its implications for compressed sensing. Comptes Rendus Mathematique, 346, 589-592.
-
7
. Baraniuk, R., Davenport, M., DeVore, R., et al. (2008) A sample proof of the restricted isometry property for random matrices. Constructive Approximation, 28, 253-263.
-
8
. Goyal, V.K., Kovacevic, J. and Kelner, J.A. (2001) Quantized frame expansions with erasures. Applied and Computational Harmonic Analysis, 10, 203-233.


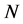 维信号
维信号
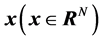 ,并可被
,并可被
 维基向量
维基向量
 表示。那么由这些基向量构成的基矩阵则为
表示。那么由这些基向量构成的基矩阵则为
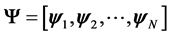 ,
,
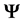 也称为稀疏字典。信号
也称为稀疏字典。信号
 可线性表示为:
可线性表示为:
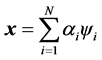 或
或
 (1)
(1)
 是信号的时域表示形式,
是信号的时域表示形式,
 称为稀疏矢量,并且
称为稀疏矢量,并且
 是信号在
是信号在
 域的等效表示形式。如果
域的等效表示形式。如果
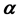 中只有
中只有
 个非零值,其余都是零,且
个非零值,其余都是零,且
 或者
或者
 中只有
中只有
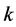 个大系数,其余系数重新排列后按指数级迅速衰减至零,那么就认为信号
个大系数,其余系数重新排列后按指数级迅速衰减至零,那么就认为信号
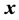 是稀疏的或可压缩的,稀疏度为
是稀疏的或可压缩的,稀疏度为
 。
。
 维信号
维信号
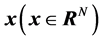 经过一个
经过一个
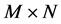 维的测量矩阵
维的测量矩阵
 后,将得到一个
后,将得到一个
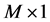 维观测值
维观测值
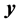 ,
,
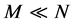 ,用公式表示如下:
,用公式表示如下:
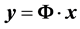

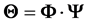 ,是一个
,是一个
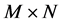 的矩阵,称为恢复矩阵。从式(3)可以看出,信号
的矩阵,称为恢复矩阵。从式(3)可以看出,信号
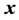 从原本的
从原本的
 维降到了
维降到了
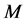 维,大大降低了信号采样点数量。
维,大大降低了信号采样点数量。
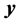 中高概率的重构出原始信号
中高概率的重构出原始信号
 或稀疏矢量
或稀疏矢量
 ,只要恢复矩阵
,只要恢复矩阵
 和稀疏矢量
和稀疏矢量
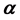 满足Candes和Tao提出的约束等距性质(Restricted Isometry Property,RIP) [6] [7] :
满足Candes和Tao提出的约束等距性质(Restricted Isometry Property,RIP) [6] [7] :

 中的有序向量集合
中的有序向量集合
 ,对于任意的
,对于任意的
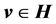 ,若是存在正实数
,若是存在正实数
 ,满足等式:
,满足等式:
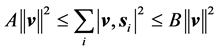
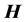 中的一个框架。其中,
中的一个框架。其中,
 和
和
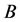 表示该框架的上下限。当
表示该框架的上下限。当
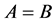 时,则称为紧框架。如果
时,则称为紧框架。如果
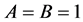 ,那么就称为标准紧框架。
,那么就称为标准紧框架。
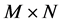 的矩阵
的矩阵
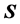 ,如果矩阵
,如果矩阵
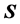 的列向量
的列向量
 满足:
满足:
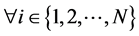 ,
,
 ;
;
 ,且
,且
 ,存在
,存在
 ,
,
 为某常数;
为某常数;
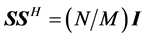 。
。
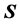 或者
或者
 的列向量构成的集合就称为等角紧框架。而ETF具有比较完美的数学表达形式,性质优良,因此在信号处理方面有着很高的应用价值。
的列向量构成的集合就称为等角紧框架。而ETF具有比较完美的数学表达形式,性质优良,因此在信号处理方面有着很高的应用价值。
 具有相同的奇异值,那么它的列向量就是一个紧框架,因此构造一个恢复矩阵对应的矩阵来逼近等角紧框架
具有相同的奇异值,那么它的列向量就是一个紧框架,因此构造一个恢复矩阵对应的矩阵来逼近等角紧框架
 。
。

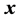 的重构在小稀疏度情况下具有非常简洁快速的过程,具体可描述如下:
的重构在小稀疏度情况下具有非常简洁快速的过程,具体可描述如下:
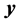 计算
计算
 ,进一步
,进一步
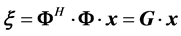 ;
;

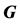 的表达式以及
的表达式以及
 可以得到列矢量
可以得到列矢量
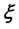 中的第
中的第
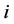 个元素
个元素
 与
与
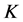 稀疏信号
稀疏信号
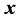 中非零元素
中非零元素
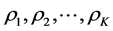 及其位置索引
及其位置索引
 之间有如下关系:
之间有如下关系:
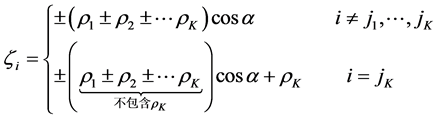
 中的相应元素
中的相应元素
 有
有
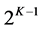 种可能的取值。当小稀疏度时,可以采用统计方法求得元素
种可能的取值。当小稀疏度时,可以采用统计方法求得元素
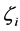 ,再根据式(7)得到对应稀疏信号
,再根据式(7)得到对应稀疏信号
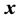 的零元素位置索引,进而确定出对应稀疏信号
的零元素位置索引,进而确定出对应稀疏信号
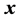 的零元素位置;而对应原始稀疏信号中的非零元素位置,矢量
的零元素位置;而对应原始稀疏信号中的非零元素位置,矢量
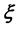 中的相应元素值则处于异类。
中的相应元素值则处于异类。
 的等角紧框架,把它写成矩阵形式为:
的等角紧框架,把它写成矩阵形式为:
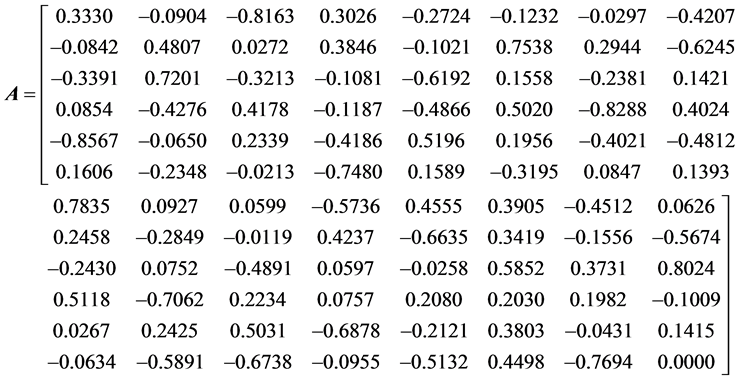
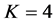 ,则能精确重建的频带压
,则能精确重建的频带压
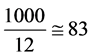 ,且信息测量点数不受
,且信息测量点数不受
 的制约。而相反,同样的信
的制约。而相反,同样的信
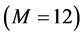 ,OMP和BP算法是不能重构原始信号的。
,OMP和BP算法是不能重构原始信号的。