空间中三维矢量（Vectors in 3D space）_三维空间向量

link管理

链接快照平台

输入网页链接，自动生成快照
标签化管理网页链接

1.1 单位矢量（Unit vector）

如下图所示，矢量

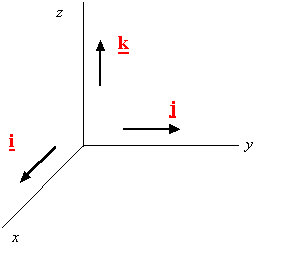
1.2 坐标基（Base vectors for a rectangular coordinate system）

三个相互正交的单位矢量

1.3 右手系（Right handed system）

由满足右手螺旋准则的三个相互正交的单位矢量构成的坐标系，上图就是一个由坐标基

2.1 矢量的坐标分量（Rectangular component of a Vector）

矢量

本文回顾三维空间中矢量的一些基本概念，虽然这些知识在高中数学中就已学到，但真的是会经常忘记1.坐标系相关内容1.1 单位矢量（Unit vector）如下图所示，矢量i−\underline{i}、j−\underline{j}、k−\underline{k}分别是长度为1的矢量（即单位矢量） 1.2 坐标基（Base vectors for a rectangular coordinate sy

超级免费矢量图搜索引擎，超过5000多个免费矢量和1亿张照片，Free Vector s.me 超级免费矢量 –最佳免费矢量艺术和正版矢量图片搜索引擎（超过5000+免费矢量图片+ 1亿个库存照片，插图，矢量和视频在一个地方）特点：1.最快的速度来帮助您找到最佳图像，帮助设计师节省时间。 2.从一个中心位置搜索最受欢迎的股票站点。 3.这是找到要在您的任何项目中使用的高质量矢量艺术的好方法。 4. 5000+质量矢量艺术免费下载。 5.提供EPS格式和AI的矢量艺术。 6.超过1亿张图片，插图，矢量和视频。经常需要做网页开发，广告设计，动画，图形设计以及各种设计人员和开发人员，损失金额是必须使用的数字，如果您仍在使用这种图形设计的PSD，建议您应该升级您的平台和设计工具，设计图像经常需要花费大量时间，可在Internet上下载有很多免费的和有照片图片的网站，什么样的免费矢量才是最好的使用方式？哪家公司提供的图像是最便宜的，并且是高质量的，我们花了三个月的时间为Google Chrome编写了此超级免费矢量，因此将其称为“超级免费矢量 ”，这是同时搜索的5000多种免费矢量来自free vector s.me以及来自（istockphotos，shutterstock，thinkstockphotos，gettyimages，photos和graphicriver）的超过1亿张股票图像。这是全球最受欢迎的图像销售公司，这7家公司提供的股票照片，仅一个查询，根据提供的结果提供的超级免费矢量，您可以比较这些图像并轻松找到所需的图像，尽管有些图像是收费的，但它们的质量很高，下载以来的最低价为$ 0.1，当然，所有free vector s.me图像均可免费使用。支持语言:English

α,β 坐标系，它的方向和定子三相绕组的位置相对固定，它的方向 A 相的产生磁势的方向，另一种是固定在转子上的旋转坐标系， d,q坐标，其中 d 轴跟单磁极的 N 极方向相同，即和磁力线 q 轴超前 d 轴 90 度下图所示。我们获取的是定子绕组上的三相电流，所以我们还需要做的 α,β坐标系中和 d,q 坐标 α,β坐标系和 A，B，C 三相之间的变换（以电流为例）。通过控制器对其速度电流环进行控制,控制 id 就相当于控制磁通,而控 iq 就相当于控制转矩。Iq 调节参考量是由速度控制器给出，经过电流环调 d，q 轴上的电压分量即 ud 和 uq。. ud 和 uq 通过 Park 逆变换。 SVPWM 空间矢量合成方法实现矢量控制量输出，达到矢量控制的． SVPWM产生原理是空间电压矢量 PWM 波产生，它具有电压利用率高、低谐波成开关次数少和功率管功耗小等特点。同时，SVPWM 还能很好的结合矢量控制为矢量控制得实现提供很好的途径，以最大限度的发挥设备的性能。

1. 点和向量的区别点是 三维空间 中的某个坐标，是绝对的，它的值是参照原点的，而向量用于表示力和速度等具有方向和大小的量，通常用具有长度和方向的线段来表示，虽然他们都具有三个分量，但对于向量，如果将向量放在坐标系中的任何位置（平移），都不会改变其性质，因为向量表示的是方向和大小，与位置距离无关，它的值是相对与基准点的。下图是三维顶点和向量的数学符号或称为列矩阵。

⑴ 矢量可以被看做一个带有箭头的单位长度直线，I方向在X轴，J方向在Y轴，K方向在Z轴。 ⑵ 矢量 I、J、K值介于1和-1之间，分别表示与X、Y、Z夹角的余弦。 ⑶I=COS (α) J=COS (β) K=COS (γ） ⑷在三坐标测量中矢量精确指明测头垂直触测被测特征的方向，即测头触测后的回退方向。矢量应用在以下方面： ①标准球的方向：球杆指向球心的方向 ②零件坐标系的建立找正：把一个三维特征的矢量作为零件坐标系的第一轴方向旋转：把一个特征的矢量作为零件坐标系的第二轴方向 ③特征矢量：特...

import Vector Field from " vector -field" ; let time = 0 ; const directionFn = ( [ x , y , z ] ) => { const n = myNoise4D ( x , y , z , time ) ; const theta = n ; const phi = n ; return [ Math . sin ( theta ) * Math . sin ( phi ) , Math . cos ( theta ) , Math . sin ( theta ) * Math . cos ( phi ) const vector Field = new Vector Field ( directionFn , [ 12 , 6 , 6 ] , 1 ) ; const frame = ( ) => { time += 0.001 ;

矢量可以被看做一个带有箭头的单位长度直线，I方向在X轴，J方向在Y轴，K方向在Z轴。矢量 I、J、K值介于1和-1之间，分别表示与X、Y、Z夹角的余弦。在三坐标测量中矢量精确指明测头垂直触测被测特征的方向，即测头触测后的回退方向。在测量时，为了表示被测元素在空间坐标系中的方向引入矢量这一概念。当长度为"1”的空间矢量投影到空间坐标系的X、Y，z三个坐标轴上时，相对应有三个投影矢量。这三个投影矢量的数值与对应轴分别为1、J、K，投影长度计算公式：I=1 矢量方向与+x夹角的余弦，I=1 矢量方向与+x夹角的

三坐标测量机工作时，定核平面的零度是很重要的一项工作。投影的工作平面不正确，评价的结果将是错误的。尤其直线元素和圆元素是二维元素，测量机先把元素的点投影到工作平面上，再拟合出元素，若工作平面选择错误，则打出的元素也会是错误的。工作平面是一个视图平面，类似图纸上的三视图，工作时从这个视图平面往外看。若测量元素在上平面，那么就是在Z平面上工作，若测量元素在右侧面，那么就是在工作平面上工作，如下图所示。测量时通常在一个工作平面上测量完所有的几何特征以后，再切换另一个工作平面，接着测量这个工作平面的几何特征。

本博文为博主原创，转载请注明出处：http://blog.csdn.net/xiemotongye/article/details/9052165 接触OpenGL和计算机图形学有一段时间了，一直想写一点东西，记录自己的学习历程，或许也能够为有意愿向计算机图形学发展的菜鸟们提供一条捷径。闲话不多说，本章主要介绍计算机图形学中三维数学的一些基础知识，主要包括2D、 3D 笛卡尔坐标系，向量、矩阵的

normals = computeNormals(vertices, faces); % Calculate the surface roughness using the SurfStat tool roughness = SurfStatCurvature(vertices, faces, normals, 'gaussian', 5); % Visualize the surface roughness trisurf(faces, vertices(:,1), vertices(:,2), vertices(:,3), roughness); colorbar; 在这个示例中，我们首先加载了一个 3D 表面网格。然后使用`computeNormals`函数计算了每个顶点的法向量。最后，使用`SurfStatCurvature`函数计算了表面的粗糙度，并使用`trisurf`函数可视化了结果。请注意，`SurfStatCurvature`函数的第四个参数指定了用于计算表面粗糙度的内核类型，可以选择`gaussian`、`mean`或`laplace`。第五个参数是内核的半径。你可以根据自己的需求选择合适的参数。

为什么是转置？一种理解方法：我们知道卷积运算通常都会用im2col的思想转化为矩阵乘法。 example：假设有一个4×4的输入图像，filter：size=3×3，stride=1，padding=0，则卷积后的结果为out_h/out_w = (4+2*0-3)/1 + 1 = 2，所以feature map为：2×2；那么以im2col的思想：4×4的输入图像会被转化为4×9的二维矩阵，过滤器转化为9×1（这里假设了通道为1，过滤器批个数为1），二维矩阵乘法（卷积）运算的结果为4×1，reshape后为2×2的feature map；现在进入反卷积的过程，我们将过滤器转置（T）后为：1×9，然后这里的反卷积运算：[4×1]·[1×9]=[4×9]，这里的4×9要通过col2im的思想 back to 像素空间，就能得到最终的特征图在像素空间的投影安装visual studio 2012，并配置opencv newgiser: 请问dll怎么查看呀？我的是3.4.1版本对极几何基本概念 qq_25245099: 好评，细致通透对极几何基本概念 zml39: